The non-force magnetic fields were first predicted by Chandrasekhar in 1956 in his well-known published work [1]. Since then there have appeared a large number of theoretical studies [5,6,15,17] with the research into various aspects of physical manifestations of non-force magnetic fields. However by now their existence in the technical physics and in laboratory experiments has not been experimentally confirmed [30]. Nevertheless the indistinct presence on the Earth of such fields was, in a sense, discovered in the natural electromagnetic field much earlier.

In 1902 at the Congress of Physicists, Professor Van Vleuten from the Holland University presented a paper informing about non-potential magnetic fields of the calm solar-daily variations of the Earth’s magnetism in the Earth’s atmosphere, where electric current is practically absent. The result obtained clearly contradicted the first Maxwell’s equation ∇ × Η = j, j = 0, ∇ × H = 0. H - Potentially. That was why Van Vleuten has called such a magnetic field “non-potential”. Her result was published fifteen years later in the Proceedings of the Physical Faculty of the Amsterdam University [2].

Van Vleutens result on the magnetic non-potential field in the Earth’s atmosphere in the calm solar-daily variations of the Earth’s magnetism was strongly supported in the monograph by Benkova [3], which contains the results of processing and interpretation of the calm solar-daily variations observed in the First International Geophysical Year (1933).

The same result concerning the non-potential magnetic fields can be found in the monograph by Aksenov [4]. These fields were called the toroidal magnetic fields obtained after processing and interpretation of the data from the Second International Geophysical Year (1957/1958).

Some difference in the terms of the discovered magnetic fields of the above-mentioned authors suggests an exact definition as well as an explanation of their physical nature, and also the whys and wherefores of their place in Physics and in the long-known Maxwell’s equations. The latter are considered to be absolutely correct not only in terms of the Earth, but also in the electro-dynamics of space. However Parker [5] indicates to the fact that applying Maxwell’s equations to the space magnetic fields has not been proved.

Non-forceful magnetic fields have no Lorentz force in the sources. Formally, this circumstance can be expressed in the following manner: F_L = [j×B] = 0.

where F_L is the Lorentz force, j is the current density, B is the magnetic induction. It is well known that in the technical physics in any experiments on the Earth with a magnetic field, the Lorentz force in its sources always exceeds zero.

F_L = [j×B] > 0

An important feature of a non-force magnetic field, according to [1,5-7], is its non-potentiality. Taking this property into account, the above-mentioned non-potential magnetic fields and toroidal magnetic fields should be referred to as the non-force magnetic fields. In order to be certain in it, it is necessary to give precise definitions to the force and the non-force electromagnetic fields, to find their position in Maxwell’s equations, to pre-determine the applicability limits of Maxwell’s equations keeping in mind the above-mentioned Parker’s “slip of the tongue”.

On the applicability limits of Maxwell’s equations

The question about the applicability limits of Maxwell’s equations in the Earth’s electrodynamics does not practically arise. However this is the long-standing question since Larmor’s work [8] that was published in 1919, in which much attention is given to the fact that the motion of a charged fluid with the velocity V in the magnetic field generates a supplementary electric field by the formula,

E´ = E + [V×B] (1)

Substituting formula (1) into the second Maxwell’s equation $\frac{\partial B}{\partial t}=-\nabla \times \left(E+[V\times B]\right)$ and having transformed the first Maxwell’s equation by multiplying from the right and left by the magnetic permeability µ, for example ∇×B = µσE, it appears possible to obtain a new equation by integrating the first and second Maxwell’s equations having excluded the electric field:

$\frac{\partial B}{\partial t}=\frac{1}{\mu \sigma }\Delta B-\nabla \times [V\times B]$ (2)

Here σ is the conductivity. Equation (2) is generally called the equation of induction with a dynamo term. This equation makes possible to specify the applicability limits of Maxwell’s equations based on the similarity criterion, i.e. the Reynolds number $R{e}_m=L\mu \sigma \left|V\right|$ . Here L is the characteristic size indicating to the location of the interface between laminar and turbulence in the magnetic field.

In the Earth’s conditions the similarity criterion $R{e}_m\approx {10}^{17}$ is close to unity due to the constraints of a characteristic size of technical devices and laboratory experiments. This makes possible to reject the second term in (2) and to obtain the equation for induction:

$\frac{\partial B}{\partial t}=\frac{1}{\mu \sigma }\Delta B$ (3)

Equation (3) is absolutely correct and reflects the electro-dynamics on the Earth and completely obeys Maxwell’s equations. This gave rise to the myth about the comprehensive scope of any electromagnetic phenomena by means of Maxwell’s electrodynamics. This is true in the technical electrodynamics on the Earth.

In the electrodynamics of space, the similarity criterion is fixed at the level $R{e}_m\approx {10}^{17}$ units [5], therefore equation (2) can be rewritten as follows:

$\frac{\partial B}{\partial t}=-\nabla \times [V\times B]$ (4)

Equation (4) and the similarity criterion $R{e}_m$ for space assume the presence of turbulence in the magnetic field. This has allowed Parker to advocate that the magnetic field in space is generated at the account of turbulence and convection with a non-uniform rotation of the space objects and is supported by the mutual generation of toroidal and poloidal magnetic fields [5].

Natural electromagnetic fields on the Earth: the main geomagnetic field (MGF) and its different variations (the variable part of S_q variations, for example) are described by the similarity criterion at the level $R{e}_m\approx {10}^3÷{10}^5$ units [5,7]. Hence, the terms in the right-hand side must not be ruled out. This deduces the natural electromagnetic fields (except for the magnetic prospecting) from the limits of standard Maxwell’s equations because in addition to diffusion and induction there may appear hydro magnetic effects caused by a possible toroidal part of electromagnetic fields. As will be shown below, this is observed in the Main geomagnetic field and its variations.

Determination of toroidal and poloidal electromagnetic fields

Determination of toroidal and poloidal electromagnetic fields originates from zero divergence of the magnetic field $\nabla \cdot H=0$ ($\nabla \cdot B=0$ ) that is valid everywhere due to the absence of magnetic charges. Following [9], the first step to determining the fields in question is the introduction of the vector A and the scalar potentials outside the source with the help of the chain of equalities:

$\nabla \cdot H=0,H=\nabla \times A,A=(Qr)+\nabla \times (Qr)$ (5)

Here $A,Q\in C^{\infty }$

Then the toroidal orthogonal decomposition of the vector A makes possible to uniquely introduce the toroidal magnetic field H_Τ using a simple relation [9]:

$H_T=\nabla \times (Qr)$ (6)

as well as the poloidal magnetic field HP using a double rotor:

$H_P=\nabla \times \nabla \times (Qr)$ (7)

These definitions make possible outside the source in unprimed coordinates (the primed coordinates belong to the source) to obtain the basic relation between the above-mentioned fields:

$\nabla \times H_T=H_P$ (8)

An apparent non-coincidence of the dimension in (8) is explained by the fact that the magnetic fields H_Τ and H_P as a scalar function $Q$ are determined outside the source. Therefore these fields have dimensional constants characterizing the sources being part in H_Τ, H_P and the scalar function $Q$ and calculated in primed coordinates.

The differential operators in (5-8) do not change the dimension of these constants being specified in non-primed coordinates.

On the other hand, if the rotor of equation (7) is calculated, it will appear possible to obtain the second relation that is symmetric to (8). Actually:

$\nabla \times H_P=\nabla \times \nabla \times \nabla \times (Qr)=-\nabla \times (\Delta Qr)=\chi H_T,$ (9)

where: $\Delta Q=-\chi Q=\{\begin{array}{l}-\frac{\gamma }{\eta }Q\text{ t=0}\\ -{(}^{i}Q\text{ t>0}\text{.}\end{array}$

Here γ is the diffusion velocity of the magnetic field, η is the magnetic viscosity, ${(i\omega \mu \sigma )}^{1/2}$ is the wave parameter of the medium, in which the magnetic field is propagating, η is the conductivity, µ is the magnetic permeability, ω is the circular frequency. With allowance for formulas (8) and (9), a pair of mutually generating magnetic fields (variable and constant) will be of the form:

∇×Η_Τ = Η_P, ∇×Η_P = χΗ_Τ (10)

provided the mutual generation is possible only in a conducting medium when the parameter χ ≠ 0 and the fields in question attain the required strengths. Relations (10) are fundamental, as they have a number of fundamental applications, which will be mentioned below.

The relationship H_Τ, H_P and the function with the scalar potential and vector potential components in spherical coordinates is given by the formulas [10]:

$H_{P\theta }=\frac{1}{r}\frac{\partial }{\partial r}\frac{\partial }{\partial \theta }(Qr)=\frac{1}{r}\frac{\partial }{\partial r}r{A}_{\phi },H_{P\phi }=\frac{1}{r}\frac{\partial }{\partial r}\frac{1}{sin\theta }\frac{\partial }{\partial \phi }(Qr)=\frac{1}{r}\frac{\partial }{\partial r}r{A}_{\theta }$ $H_{Pr}=-\frac{1}{r^{2}sin\theta }\left(\frac{\partial }{\partial \theta }sin\theta \frac{\partial (Qr)}{\partial \theta }+\frac{\partial }{\partial \phi }\frac{1}{sin\theta }\frac{\partial (Qr)}{\partial \phi }\right)=-\frac{1}{rsin\theta }\left(-\frac{\partial }{\partial \theta }\frac{1}{sin\theta }{A}_{\phi }+\frac{\partial A_{\theta }}{\partial \phi },\right)$ $H_{T\theta }=\frac{1}{rsin\theta }\frac{\partial }{\partial \phi }(Qr)=\frac{1}{rsin\theta }\frac{\partial }{\partial \phi }{A}_r,H_{T\phi }=-\frac{1}{r}\frac{\partial }{\partial \theta }(Qr)=-\frac{1}{r}\frac{\partial }{\partial \theta }{A}_r$ (11)

Formulas (11) prove the possibility of describing toroidal and poloidal magnetic fields both with the help of one scalar function $Q$ and with the three components of the vector potential A. This possibility will be used when explaining the experiments with non-force electromagnetic fields.

To define the toroidal and poloidal electric fields at t > 0, where is the time, it is necessary to make use of the standard Maxwell’s equations with Larmor’s correction:

$\nabla \times H=\sigma E^{\prime }+\epsilon \frac{\partial E^{\prime }}{\partial t}+,\nabla \times E^{\prime }=-\mu \frac{\partial B}{\partial t},\nabla \cdot (H,E^{\prime })=0.$ (12)

Here σ, µ, ω are the constants, E´is borrowed from (1), ${\sigma }^{\prime }=\sigma +i\omega \epsilon$ . In addition, it is needed to make use of the vector potential decomposition from (5):

$H=\nabla \times A,E^{\prime }=-i\omega \mu A+\nabla \phi$ (13)

In formula (13) it is also required to apply the Lorentz calibration for the vector potential:

$\phi =\frac{1}{{\sigma }^{\prime }}\nabla \cdot A$ (14)

In this case it appears possible to obtain the general formula:

$E^{\prime }=-i\omega \mu (Qr)+i\omega \mu \nabla \times (Qr)+\frac{1}{{\sigma }^{\prime }}\nabla \nabla \cdot (Qr)+\frac{1}{{\sigma }^{\prime }}\nabla \nabla \cdot \nabla \times (Qr)$ (15)

The latter term in (15) is identically equal to zero. It is possible to introduce into the rest terms the toroidal and poloidal electric fields in the following manner [10]:

${E^{\prime }}_T=-i\omega \mu \nabla \times (Qr),{E^{\prime }}_P=-i\omega \mu (Qr)+\frac{1}{{\sigma }^{\prime }}\nabla \nabla \cdot (Qr)$ (16)

In the second formula in (16), the inductive term $-i\omega \mu (Qr)$ is not typical of the poloidal potential field ${E^{\prime }}_P$ and is compensated according to the following theorem.

Theorem 1

The induction term $-i\omega \mu (Qr)$ is compensated by the term $\frac{1}{{\sigma }^{\prime }}\nabla \nabla \cdot (Qr)$ provided that

Proof.

For the proof, let us partition the space into two parts with respect to the regular boundary S. The inner part is represented by the function $Q^i(r,\theta ,\phi ,t)$ and its decomposition:

$Q^i(r,\theta ,\phi ,t)={\displaystyle \sum _{n=1}^{\infty }{K}_{n+1/2}(\text{æ}\frac{r}{R})S_n(\theta ,\phi )}$ (17)

Here $K_{n+1/2}(\text{æ}\frac{r}{R})$ is the added Bessel function of the semi-index $\text{æ}=i\omega \mu \sigma R^2-\epsilon {\omega }^2\mu R^2,S_n(\theta ,\phi )={\displaystyle \sum _{m=0}^n{A}_n^m{P}_n^m}(\cos \theta )e^{im\phi },S_n(\theta ,\phi )\in C^{\infty }$ , R is the radius of the domain separated by the regular boundary S, r is the current radius.

The external part is represented by the function $Q^e(r,\theta ,\phi ,t)$ :

$Q^e(r,\theta ,\phi ,t)={\displaystyle \sum _{n=1}^{\infty }{I}_{n+1/2}(\text{æ}\frac{r}{R})S_n(\theta ,\phi )}$ (18)

Here and in (17) $A_n^m$ are the complex constants, $P_n^m(\cos \theta )$ are the spherical functions. The factor e^iωt in the right and left hand sides of formulas (17) and (18) is omitted. The arguments of the Bessel functions are separated from zero and infinity.

For the proof we will need the first and second derivatives of the Bessel functions being part in (17) and (18). In order not to complicate the presentation with formulas, we are giving the proof only for the function $Q^i(r,\theta ,\phi ,t)$ :

$\begin{array}{l}\frac{\partial Q^i}{\partial r}={\displaystyle \sum _{n=1}^{\infty }{S}_n(\theta ,\phi ){K^{\prime }}_{n+1/2}(\frac{\text{æ}r}{R})={\displaystyle \sum _{n=1}^{\infty }{S}_n(\theta ,\phi )}}\left[-\frac{\text{æ}}{R}{K}_{n-1/2}(\frac{\text{æ}r}{R})-\frac{n+1/2}{r}{K}_{n+1/2}(\frac{\text{æ}r}{R})\right],\\ \frac{{\partial }^2{Q}^i}{\partial r^2}={\displaystyle \sum _{n=1}^{\infty }{S}_n(\theta ,\phi ){K^{″}}_{n+1/2}(\frac{\text{æ}r}{R})}={\displaystyle \sum _{n=1}^{\infty }{S}_n(\theta ,\phi )}\left[(\frac{(n+1/2)(n+3/2)}{r^2}+\frac{{\text{æ}}^2}{R^2})K_{n+1/2}(\frac{\text{æ}r}{R})+\frac{\text{æ}}{rR}{K}_{n-1/2}(\frac{\text{æ}r}{R})\right].\end{array}$

Let us transform the radial component from (16) by omitting the upper prime:

$E_{\mathrm{Pr}}^i=-i\omega \mu Q^{i}r+\frac{1}{{\sigma }^{\prime }}\frac{\partial }{\partial r}\frac{1}{r^2}\frac{\partial }{\partial r}{r}^2{Q}^{i}r=\frac{1}{{\sigma }^{\prime }}\left[-{\text{<mover accent="true"> æ <mo>¯</mo> </mover>}}^{2}Qr+r\frac{{\partial }^2{Q}^i}{\partial r^2}+4\frac{\partial Q^i}{\partial r}\right]$ (20)

In (19) and (20) the arguments of the function $Q^i(r,\theta ,\phi ,t)$ are omitted for reasons of economy. Now we calculate the radial component $E_{\mathrm{Pr}}^i$ :

$\begin{array}{l}{E}_{\mathrm{Pr}}^i=\frac{1}{{\sigma }^{\prime }}{\displaystyle \sum _{n=1}^{\infty }{S}_n(\theta ,\phi )[-{\text{<mover accent="true"> æ <mo>¯</mo> </mover>}}^{2}r{K}_{n+1/2}(\frac{\text{æ}r}{R})+r\left(\frac{(n+1/2)(n+3/2)}{r^2}+\frac{{\text{æ}}^2}{R^2}\right)}{K}_{n+1/2}(\frac{\text{æ}r}{R})+\frac{\text{æ}}{R}{K}_{n-1/2}(\frac{\text{æ}r}{R})-\\ -\frac{4\text{æ}}{R}{K}_{n-1/2}(\frac{\text{æ}r}{R})-\frac{4(n+1/2)}{r}{K}_{n+1/2}(\frac{\text{æ}r}{R})].\end{array}$

In (21) it is required to reduce similar terms with allowance for ${\text{æ}}^2={\text{<mover accent="true"> æ <mo>¯</mo> </mover>}}^2{R}^2$ . As a result we arrive at:

${\overline{F}}_L=[\chi H_T\times \mu H_T]\equiv 0,\text{ э}\text{.д}\text{.с}.={\displaystyle \underset{L}{\oint }(E_P\cdot dl)}={\displaystyle \underset{W}{\int }(\nabla \times E_P\cdot ds)}\equiv 0$ (22)

It is not difficult to notice that the induction term in (22) vanishes. Only the potential part remains there. A similar result is valid for $E_{\mathrm{Pr}}^e$ . The Theorem has been proved.

Therefore, toroidal and poloidal electric fields be defined as follows [10]:

${E^{\prime }}_T=-i\omega \mu \nabla \times (Qr),{E^{\prime }}_P=\frac{1}{{\sigma }^{\prime }}\nabla \nabla \cdot (Qr)$ (23)

The relation of the spherical components of these fields to the corresponding components of the vector potential in spherical coordinates will be of the form [10]:

$\begin{array}{l}{E}_{T\theta }=-i\omega \mu \frac{1}{rsin\theta }\frac{\partial }{\partial \phi }(Qr)=-i\omega \mu A_{\theta },E_{T\phi }=-i\omega \mu \left(-\frac{1}{r}\frac{\partial }{\partial \theta }(Qr)\right)=-i\omega \mu A_{\phi },E_{P\theta }=\frac{1}{{\sigma }^{\prime }}\frac{1}{r}\frac{\partial }{\partial \theta }\frac{1}{r^2}\frac{\partial }{\partial r}{r}^2(Qr)=\frac{1}{{\sigma }^{\prime }}\frac{1}{r}\frac{\partial }{\partial \theta }\frac{1}{r^2}\frac{\partial }{\partial r}{r}^2{A}_r,\\ E_{P\phi }=\frac{1}{{\sigma }^{\prime }}\frac{1}{rsin\theta }\frac{\partial }{\partial \phi }\frac{1}{r^2}\frac{\partial }{\partial r}{r}^2(Qr)=\frac{1}{{\sigma }^{\prime }}\frac{1}{rsin\theta }\frac{\partial }{\partial \phi }\frac{1}{r^2}\frac{\partial }{\partial r}{r}^2{A}_r,E_{Pr}=\frac{1}{{\sigma }^{\prime }}\frac{\partial }{\partial r}\frac{1}{r^2}\frac{\partial }{\partial r}{r}^2(Qr)=\frac{1}{{\sigma }^{\prime }}\frac{\partial }{\partial r}\frac{1}{r^2}\frac{\partial }{\partial r}{r}^2{A}_r.\end{array}$ (24)

According to formulas (24), the toroidal and poloidal electric fields outside a source can also be determined with the help of one scalar potential $Q$ or three components of the vector potential A in respective derivatives.

Non-force and force properties of toroidal and poloidal electromagnetic fields

The elucidation of the principal properties of the toroidal and poloidal electromagnetic fields will be presented based on [9,12,13]. To this end, it is required to calculate the Lorentz force of the following pairs of the electromagnetic field H_P, H_T as well as H_T, E_P:

$\begin{array}{l}{F}_L=[j_T\times B_P]=[\sigma E_T\times \mu H_P]\ne 0,\text{ э}\text{.д}\text{.с}\text{.=}{\displaystyle \underset{L}{\oint }(E_T\cdot dl})={\displaystyle \underset{W}{\int }(\nabla \times E_T\cdot ds)}=-\mu {\displaystyle \underset{W}{\int }(\frac{\partial H_P}{\partial t}\cdot ds)}\ne 0\\ F_L=[j_T\times B_P]=[\sigma E_T\times \mu H_p]\ne 0,\text{ э}\text{.д}\text{.с}.\text{=}\underset{L}{\int }(E_T\cdot dl)=\underset{W}{\int }(\nabla \times E_T\cdot ds)=\mu \underset{W}{\int }(\frac{\partial H}{\partial t}\cdot ds)\end{array}$ (25)

Formulas (25) reflect the Lorentz non-zero force for the first pair of the force electromagnetic fields H_P, H_T. The Lorentz force for the second pair is written down in a similar way:

${\overline{F}}_L=[\chi H_T\times \mu H_T]\equiv 0,\text{ э}\text{.д}\text{.с}.={\displaystyle \underset{L}{\oint }(E_P\cdot dl)}={\displaystyle \underset{W}{\int }(\nabla \times E_P\cdot ds)}\equiv 0$ (26)

In formulas (26), the Lorentz forceis identically equal to zero due to the fact that the vector product of the toroidal magnetic field with itself is equal to zero in the context of the coinciding direction. The constants χ and µ do not change their direction, ?E.D.S of induction is also identically equal to zero due to the equality to zero of the rotor of the poloidal electric field because the poloidal electric field is a gradient of a certain scalar assigned by divergence of the vector . Moreover, the determination of non-force and force modifications coincides from the physical standpoint with the determination of modifications of the magnetic and electric forms from [14]:

$H_P^{MT}=\nabla \times \nabla \times (Qr),E_T^{MT}=-i\omega \mu \nabla \times (Qr),H_T^{ET}=\nabla \times (Qr),E_P^{ET}=\frac{1}{\sigma }\nabla \nabla \cdot (Qr)$ (27)

As we are able to verify, the appearance in (27) of non-force fields is not extraordinary in physics. However it is needed to elucidate the kind of sources of these fields both on the Earth and in Space.

On the sources of non-force electromagnetic fields on the earth and in space

Due to the Reynolds similarity criterion $R{e}_m\le 1$ and equation (3), non-force electromagnetic fields on the Earth have not manifested themselves in the experiment. However many published works deal with their theoretical study [6,15]. Among the publications, of special interest is Kauling’s paper [16]. In it, an important result from the practical standpoint is obtained that reduces in our terms to the following: plain and cylindrical symmetries of the electromagnetic field sources on the Earth do not bring about the generation of non-force electromagnetic fields. Kauling’s result can be supplemented by the following two theorems.

Theorem 2

A non-turbulent vector field ∇ × Η = 0 under the condition $\nabla \cdot H=\rho$ at ρ = const does not admit generation of the vector field $H_T=\nabla \times (Qr)$ if $H\ne 0,H_T,H_P\ne 0$ .

In fact, the helicity $H\cdot \nabla \times H$ in the non-turbulent vector field equals zero because of ∇ × Η = 0, while the helicity of the vector field, H_T by definition is not equal to zero: $H_T\cdot \nabla \times H_T=H_T\cdot H_P\ne 0$ The absence of coincidence of the helicities due to the influence of the recursion symmetry [16] excludes the mutual generation of the vector fields H_T and H_P [6,16].

Theorem 3

In the solenoid vector field $\nabla \cdot H=0,\nabla \times H=P$ , (Ρ is the vector field), the vector field $H_T=\nabla \times (Qr)$ can be generated if $H\ne 0,H_T,H_P\ne 0,P\ne 0$

In fact, the helicities of the vector fields H_T H_P do not equal zero. The helicity of the solenoid field Η is not equal to zero $H\cdot \nabla \times H\ne 0$ because of ∇ × Η = P.

The helicity of the vector field H_T is also not equal to zero $H_T\cdot \nabla \times H_T\ne 0$ because of ∇ × H_T = H_P. The presence of helicities in both vector fields assists in their mutual generation at the expense of the relations:

$\nabla \times H_T=H_P,\nabla \times H_P=\nabla \times \nabla \times \nabla \times (Qr)=-\nabla \times (\Delta Qr)=\chi \nabla \times (Qr)=\chi H_T$ (28)

Here $\Delta Q=-\chi Q,\chi =const$ (9).

The physical interpretation of Theorems 2 and 3 consists in the following. A toroidal magnetic field cannot arise (Theorem 2) in the presence of magnetic masses as sources of a magnetic field. If both toroidal and poloidal magnetic fields are simultaneously present, then under certain conditions in the intensities Η_Τ,P, and if the constant χ ≠ 0 is not equal to zero, the mutual generation of the above fields is possible. Theorem 3 confirms Parker’s result [5], concerning the cosmic magnetic fields, whose mutual generation of Η_Τ,P, along with the turbulence, convection and non-uniform rotation of cosmic objects occupies a prominent place.

In the technical physics, due to small characteristic sizes of L on the Earth ${\mathrm{Re}}_m\le 1_{}$ , the generation conditions Η_Τ according to Parker cannot be fulfilled. Therefore the question arises about the sources of the toroidal non-force magnetic field Η_Τ in the Earth’s natural electromagnetic field. Keeping in mind Kauling’s “forbidden” theorem [16] one should turn to the spherical electric currents, whose full density in spherical layers or on spherical surfaces with its toroidal components can generate Η_Τ .

Theorem 4

The source of the toroidal non-force magnetic field Η_Τ and of the force magnetic field Η_P are the toroidal components of the full electric current j ≠ 0.

In fact, the operator of the full electric current, as is known, is of the form:

$j=(\nabla \nabla \cdot -\nabla \times \nabla \times )A$ (29)

Let us map this operator onto the axis of the spherical coordinate system, having fixed only toroidal components of the current:

$\begin{array}{l}-j_{\theta }^{\text{П}}=\frac{{\partial }^2{A}_{\theta }}{\partial r^2}+\frac{2\partial A_{\theta }}{r\partial r}+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^2{A}_{\theta }}{\partial {\phi }^2}+\frac{1}{r^2}\frac{{\partial }^2{A}_{\theta }}{\partial {\theta }^2}-\frac{\cos \theta }{r^2\sin \theta }\frac{\partial A_{\theta }}{\partial \theta }-\frac{A_{\theta }}{r^2{\sin }^2\theta }-\\ 2\frac{\cos \theta }{r^2{\sin }^2\theta }\frac{\partial A_{\phi }}{\partial \phi }+\frac{2\partial A_r}{r^2\partial \theta },\end{array}$ $\begin{array}{l}-j_{\phi }^{\text{П}}=\frac{1}{r\sin \theta }\frac{\partial }{\partial \theta }\sin \theta \frac{\partial A_{\phi }}{\partial \phi }+\frac{1}{r^2\sin \theta }\frac{{\partial }^2{A}_{\phi }}{\partial {\phi }^2}+\frac{1}{r}\frac{{\partial }^{2}r{A}_{\phi }}{\partial r^2}+\frac{\cos \theta }{r^2{\sin }^2\theta }\frac{\partial A_{\theta }}{\partial \phi }-\\ -\frac{\cos \theta }{r^2\sin \theta }\frac{\partial A_{\phi }}{\partial \phi }+\frac{1}{r^2}\frac{\partial }{\partial \theta }\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\sin \theta A_{\phi }-\frac{1}{r}\frac{{\partial }^2{A}_{\phi }}{\partial \theta \partial \phi }+\frac{2}{r^2\sin \theta }\frac{\partial A_r}{\partial \phi }.\end{array}$ (30)

If we turn to decomposition (5), it will be possible to express the spherical components of the vector potential via the scalar function $Q$ as follows:

$A_{\theta }=\frac{1}{\sin \theta }\frac{\partial Q}{\partial \phi };A_{\phi }=-\frac{\partial Q}{\partial \theta };A_r=rQ.$ (31)

By definition (6), the components of the toroidal magnetic field are of the form:

$H_{T\theta }=\frac{1}{\sin \theta }\frac{\partial Q}{\partial \phi };H_{T\phi }=-\frac{\partial Q}{\partial \theta };H_{Tr}\equiv 0.$ (32)

According to formulas (30), the projections of the equation for the full current on the axis of the spherical coordinate system among their terms have the following expressions:

$\frac{2\partial A_r}{r^2\sin \theta \partial \phi }=\frac{2}{r\sin \theta }\frac{\partial Q}{\partial \phi }=\frac{2}{r}{H}_{T\theta };\frac{2\partial A_r}{r^2\partial \theta }=\frac{2}{r}\frac{\partial Q}{\partial \theta }=-\frac{2}{r}{H}_{T\phi }$ (33)

The right-hand sides of expressions (33) with allowance for formulas (32) are just doubled components of the toroidal magnetic field referred to a current radius, thus giving them the dimension of the current density.

Thus, the toroidal components of the spherical density of the current always generate toroidal non-force components of the toroidal magnetic field. This fact (Theorem 4) is of importance for the domains with low values of the similarity criterion, because in such domains for the generation of a non-force toroidal magnetic field there is no need in the turbulence in the magnetic field, as well as in the convection of a substance and in the non-uniform rotation of cosmic objects as this takes place in [5]. The spherical electric current is sufficient because according to Theorem 4 such a current simultaneously generates both the poloidal force and the toroidal non-force magnetic fields. The attempts to reproduce a non-force magnetic field in the laboratory experiment, described in [17], were not a success. It was necessary to rearrange the experiment to creating the toroidal spherical current, but not to reproduce the turbulence in the magnetic field. Any attempts to “twist” the force lines of the magnetic field in a sophisticated way are only theoretically possible [15], but are unlikely to be reproduced in an experiment because of small values of the characteristic size L in the Earth’s conditions according to the similarity criterion ${\mathrm{Re}}_m=L\mu \sigma \left|V\right|\le 1$ .

Some essential disagreements between Parker’s and Alfven’s concepts [5,18] concerning the primary source of the magnetic fields in the outer space can be smoothed with the help of Theorem 4 which holds that the toroidal non-force magnetic field can be generated by spherical currents even in the absence of the turbulence in magnetic fields. Strong toroidal currents are surely present on the surface of the stars as well as on the Sun’s surface. Therefore the original occurrence of the non-force magnetic field is apparently due to the electric currents. Then at the expense of the induction speed-up of the currents and field there arise just the effects considered by Parker and many other researchers before and after his considerations.

Not a simpler situation holds in the electric field. According to definitions (24), the toroidal force electric field is generated by the toroidal electric currents according to the formulas:

$\nabla \times H_P=\chi H_T=\sigma (\gamma \mu H_T)=\sigma E_T=j_T,\nabla \times H_P=\chi H_T={(i\omega \mu \sigma )}^{1/2}{H}_T=\sigma \left({\left(\frac{\omega \mu }{\sigma }\right)}^{1/2}{H}_T\sqrt{i}\right)=\sigma E_T+j_T^{CT}=j_T$ (34)

Here: $(\gamma \mu H_T)=E_T$ в V/m, $\left({\left(\frac{\omega \mu }{\sigma }\right)}^{1/2}{H}_T\sqrt{i}\right)=\frac{(i+1)}{\sqrt{2}}{\left(\frac{\omega \mu }{\sigma }\right)}^{1/2}\cdot H_T=E_T$ в V/m.

In the alternating field, E_Τ is a complex value. An electric field also arises owing to Larmor’s effect [8] when a charged fluid is moving in the magnetic field. A normal to a regular boundary component of the electric field $E_n-i\omega \mu Qr=-i\omega \mu A_r$ according to Theorem 1 is compensated by a potential field of charges appearing at regular boundaries.

The potential poloidal part of the electric field E_P from (24) is completely due to electric charges arising at the interface of conductors and the electric current or due to the charges arising by other reasons.

Boundary conditions for toroidal non-force and poloidal force electromagnetic fields

The boundary conditions at regular boundaries for the magnetic and electric fields of the above-discussed types practically do not differ from standard boundary conditions for the magnetic and electric fields determined and substantiated earlier in [14]. At regular boundaries, the behavior of magnetic and electric fields satisfies the following relations:

$(H_P^1-H_P^2)|{}_{Г}=0,(H_T^1-H_T^2)|{}_{Г}=0,E_T^1-E_T^2|{}_{Г}=0,E_{Tn}|{}_{Г}=0,E_{Pn}^1=\frac{{\sigma }_E}{{\sigma }^{\prime }}{E}_{Pn}^2$ (35)

Here: l is the upper part of the regular boundary, 2 is the lower part of the regular boundary, ${\sigma }^{\prime }$ is the conductivity of the upper part of the space above the boundary, σ_E is the conductivity of the space below the regular boundary.

The behavior of the toroidal non-force and poloidal force fields at the regular boundary is associated with applying these fields to concrete problems arising on the Earth, such as the presence or absence of the toroidal non-force magnetic and the poloidal electric fields of natural origin in the Earth’s atmosphere, in the Earth’s interior, in the cosmic space [5,6,10].

Generalized electrodynamics equations for toroidal and poloidal electromagnetic fields

The electrodynamics of the above-mentioned fields is somewhat different from Maxwell’s standard electrodynamics. Here we present the equations from the author’s publications [4,7,9,11,12]:

$\nabla \times H_P=j_T+j_T^{CT},\nabla \times H_T=H_P,\nabla \times {E^{\prime }}_T=-\frac{\partial B_P}{\partial t},\nabla \times {E^{\prime }}_P=0,\nabla \cdot (H_P,H_T)=0,\nabla \cdot ({E^{\prime }}_T,{E^{\prime }}_P)=0,D_{P,T}=\epsilon E_{P,T},B_{P,T}=\mu H_{P,T}$ (36)

Equations (36) in their form are close to Maxwell’s standard equations, although they have in their structure the effects non-intrinsic of standard equations. For example, the electric field in its composition contains Larmor’s effect as $E^{\prime }=E+[V\times B].$ . The magnetic fields Η_T, Η_P, according to Theorem 4, are excited by toroidal currents. The toroidal magnetic fields in a non-current domain are non-potential in any medium at the expense of ∇ × Η_T = Η_P. By the same reason, they are not affected by the skin effect. The poloidal electric field is potential $\nabla \times {E^{\prime }}_P=0$ . Vortices of the toroidal non-force magnetic field generate the force magnetic field because of ∇ × Η_T = Η_P but not due to the electric current. The induction of the poloidal magnetic field $\frac{\partial B_P}{\partial t}$ contains hydromagnetic effects due to Larmor’s effect (formula (2)). Vortices of the poloidal magnetic field due to ∇ × Η_P = χΗ_Y =j_T in addition to induction and diffusion in certain conditions can generate toroidal magnetic fields in conducting media. Equations (36) allow the mutual generation of magnetic fields owing to (10). In the description of experiments, we will demonstrate other properties of the toroidal and poloidal electromagnetic fields.

Physical modeling of toroidal and poloidal electromagnetic fields

The mathematical description of the toroidal non-force and poloidal force fields has been presented above using the toroidal decomposition of the vector potential (formula (5)). As for the physical modeling, it is proposed in [6] by introducing two scalar potentials used separately for the toroidal magnetic field (the function T as a source) and the poloidal magnetic field (the function P). At first glance, such an approach is justified; however, from the mathematical standpoint it involves difficulties when proving the mutual generation of the toroidal and poloidal magnetic fields.

What are the toroidal magnetic fields as physical objects? It should be recalled that the toroidal electromagnetic fields are two-component objects of the form:

$H_T=(H_{T1};H_{T2};0),E_T=(E_{T1};E_{T2};0).$ (37)

The toroidal electric currents are also two-component. Their density of the current:

$J_T=(J_{T1};J_{T2};0),$ (38)

can take place on 2D surfaces or on uniform conductivity layers: plane, cylindrical, spherical, etc.

In order to physically reliably introduce the toroidal magnetic fields into the electromagnetic field theory, it is necessary to make use of the empirical definitions of these fields [6]. To avoid suspicion in non-coincidence of the dimension of magnetic fields in their determination in the form ([6]):

$H=H_T+H_P=\nabla \times (T\cdot r)+\nabla \times \nabla \times (P\cdot r).$ (39)

We should explain what the author [6] meant when determining these fields.

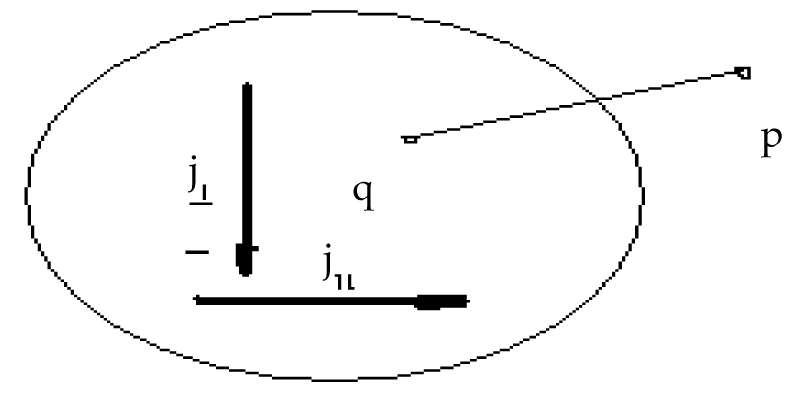
Figure 1 presents the projections of electric current components on the vertical and horizontal planes that are within the limits of a source. According to figure 1, the toroidal two-component magnetic field Η_Τ is, in fact, determined at the point p(r, θ, ϕ) outside the source of the vertical current j_T, where r, θ, ϕ are the spherical coordinates as follows:

$H_T={\nabla }_P\times (T\cdot r)$ (40)

Where T (r, θ, ϕ) is an arbitrary scalar function whose mean at the surface S is equal to zero $\langle T(r,\theta ,\phi )\rangle =0$ . Its expansion in terms of spherical functions is of the form:

$T(r,\theta ,\phi )={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n\psi (r)A_n^m{P}_n^m(\cos \theta )e^{im\phi }}}$ (41)

The complex factors $A_n^m$ have the following physical sense [10]:

$A_n^m={\displaystyle \underset{W}{\int }{\psi }_n(r^{\prime })}{J}_{\perp }(q)P_n^m(\cos {\theta }^{\prime })\cos m{\phi }^{\prime }d{w}^{\prime }$ (42)

where $J_{\perp }(q)$ is the complex function of the vertical current density.

The complexity of the current density provides the complexity of the constant factor $A_n^m$ which is needed for the completeness of expansion (41). The term containing $m{\phi }^{\prime }$ will not be written down in the context of saving room. In formulas (40)-(42), only the constant factors have a dimension because they include the current density with a physical value. These factors are determined from the magnetic field, therefore their dimension coincides with that of the magnetic field from the left-hand side of formula (40). Differentiation in (40) by means of the rotor is done by the non-dashed coordinates of the point p(r, θ, ϕ), hence the differentiation does not distort the dimension of the constant factors $A_n^m$

The poloidal magnetic field is introduced using the double rotor because it is three-component (the current $J_{\perp }(q)$ is plane), and the differentiation is also done at the points p(r, θ, ϕ):

$H_P={\nabla }_P\times {\nabla }_P\times (P\cdot r)$ (43)

Here:

$P(r,\theta ,\phi )={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n{\psi }_n(r^{\prime })}}{B}_n^m{P}_n^m(\cos {\theta }^{\prime })e^{im{\phi }^{\prime }}$ (44)

where $J_{\perp }(q)$ is the complex plane current, and

$B_n^m={\displaystyle \underset{W}{\int }{\psi }_n(r^{\prime })J_{\parallel }(q)P_n^m(\cos {\theta }^{\prime })}\cos m{\phi }^{\prime }d{w}^{\prime }$ (45)

The term containing $\sin m{\phi }^{\prime }$ is not written down here. The differentiation in the double rotor in (43) is also done at the points p(r, θ, ϕ) and does not change the dimension of the constants $B_n^m$ . Their dimension coincides with the dimension of Η_P as they are determined from this field. The double or triple application of the rotor to expressions (40) or (41) does not change the dimension of the sources that are part of the constants $A_n^m$ and $B_n^m$ because this application is done by non-dashed coordinates.

The revealed physical essence of toroidal and poloidal magnetic fields empirically introduced in [6] at the points outside the source completely confirms the author’s conclusion [6] except that expression (46) generates a poloidal field from the source that is a part of the function T(r, θ, ϕ) but not of the function p(r, θ, ϕ).

${\nabla }_P\times H_T={\nabla }_P\times {\nabla }_P\times (T\cdot r)={\tilde{H}}_P$ (46)

However the source of the function is the vertical current (Figure 1), which according to (40), generates only a two-component toroidal magnetic field. This remark should be taken into consideration when determining the toroidal and poloidal magnetic fields with the help of one scalar function, containing according to definition (38), only the toroidal current source.

In the above-said as well as in his earlier studies, the author offers to make use of an orthogonal decomposition of the vector potential of the form:

$\nabla \cdot H=0,\nabla \times A=H,A=(Q\cdot r)+\nabla \times (Q\cdot r),$ (47)

which characterizes only toroidal currents.

Here: H is the magnetic field, A is the vector potential, $Q$ is the scalar function of three variables. In this case, the toroidal magnetic field is determined as follows:

$H_T=\nabla \times (Q\cdot r).$ (48)

The poloidal magnetic field is determined in a similar manner.

$H_P=\nabla \times \nabla \times (Q\cdot r).$ (49)

Hence, the basic relations for a two-module magnetic field will look like:

$\nabla \times H_T=H_P,\nabla \times H_P=\nabla \times \nabla \times \nabla \times (Q\cdot r)=-\nabla \times (\Delta Q\cdot r)=\chi H_T,$ (50)

where:

$\Delta Q=\chi Q=\{\begin{array}{l}-\frac{\gamma }{\eta }Qt=0,\\ -{(}^{i}t>0.\end{array}$ (51)

Here: γ is the diffusion rate of the field, η is the magnetic viscosity, ${(i\omega \mu \sigma )}^{1/2}$ is the wave parameter of the medium, where a variable magnetic field propagates, σ is the conductivity of the medium, µ is the magnetic permeability of the medium, ω is the angular velocity of the variable field.

This approach, as was shown above, results in the formula for the self-generation of toroidal and poloidal electromagnetic fields (10).

Generalization of the fundamental theorem of uniqueness of the Helmholtz vector field decomposition to toroidal and poloidal electromagnetic fields

The generalization of the well-known Helmholtz theorem of uniqueness [19] to the non-force and the force magnetic fields, Η_Τ and Η_P respectively, is because of the fact that the non-force toroidal magnetic fields at a regular boundary are two-component (formula (32)). The all-important factor is the absence in them of a normal component at regular boundaries, surrounding the regions with a magnetic field. A well-known statement of the Helmholtz problem is considered in [19] in the following way: let V be a finite open spatial domain, restricted by the regular surface S, whose positive normal is uniquely defined at each point of the surface. In this case the following theorems are valid.

Theorem 5. (Theorem of decomposition)

If the divergence and rotor of the field F(r) are determined at each point $\left|r\right|$ of the domain V, then everywhere in V the function F(r)can be presented as sum of the divergent-free field F₁(r) and the solenoidal field F₂(r)

where: ∇ × F₁(r) = 0, ∇ . F₂(r) = 0

Theorem 6. (Theorem of uniqueness)

The function F(r) is uniquely defined with a supplementary condition of specifying the normal component $F(r)\frac{ds}{\left|ds\right|}$ of the function F(r) at each point of the surface S.

Effective tracking of the function F(r) with the above data reduces to solving differential partial derivative equations with certain boundary conditions.

As opposed to the above-formulated statement of the problem, we are interested only in the solenoidal part of the magnetic field, whose tangential to the surface components S contain the toroidal part. On the other hand, the domain V will be considered to be a sphere with a regular boundary containing an exterior continuous normal given at each point. In the case in question, Theorem 6 can be re-formulated to the considered problem, and the proof of this new theorem will be sought for without solving the corresponding differential equations and proving new boundary conditions in addition to the existence of the normal component H_PN(r) at each point of the surface S. The proof of this theorem was first presented in [24].

Theorem 7

The solenoidal vector field H in the spherical domain V (in the sphere with the surface S and of radius R) is uniquely reconstructed by the following expression:

$H=H_T+H_P=\nabla \times (Qr)+\nabla \times \nabla \times (Qr)$ (52)

If the normal component H_N(r) on S V is known, and the function $Q(r,\theta ,\phi )\in C^{\infty },$ whose mean $\langle Q\rangle =0$ on S, as well as H, H_T,H_P ≠ 0 and ∇ × Η_T = H_P everywhere.

Here the mean: $\langle Q\rangle ={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle {\int }_0^{\pi }Q\sin \theta d\theta d\phi =0.}}$

In fact, if the vector field Η corresponds to (52), then for proving the uniqueness of decomposition (52) it is needed to express the function Q via the initial normal component of the vector field Η_P or ∇ × Η_Τ

For example,

$\begin{array}{l}(r\cdot H_P)=r\cdot \nabla \times \nabla \times (Qr)=r\cdot \left\{\nabla \nabla \cdot (Qr)-{\nabla }^2(Qr)\right\}=r\cdot \left\{\nabla [r\cdot \nabla Q+3Q]-2\nabla Q-r{\nabla }^{2}Q\right\}\\ r^2{\nabla }^{2}Q+r\cdot \nabla (r\cdot \nabla Q)+r\cdot \nabla Q=-r^2{\nabla }^{2}Q+\frac{\partial }{\partial r}(r^2\frac{\partial Q}{\partial r})=-DQ,(r\cdot \nabla \times H_T)=r\cdot \nabla \times \nabla \times (Qr)=-DQ.\end{array}$ (53)

Here D is the direct operator (the Beltrami operator), defined in (53), namely:

$D=\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\sin \theta \frac{\partial }{\partial \theta }+\frac{1}{{\sin }^2\theta }\frac{{\partial }^2}{\partial {\phi }^2},$ (54)

That is a part of the Laplace operator without radial derivatives. From (53) it follows that

$Q=-D^{-1}(r\cdot H_P)=-D^{-1}(r\cdot \nabla \times H_T)$ (55)

Where D is the inverse operator to the operator D, which is subject to determination. With allowance for formula (53), it is possible to show that if there are employed two arbitrary scalar functions of the form $A(r)=(Pr)+\nabla \times (Qr)$ , then because of the fact that the vector field Η_Τ does not contain a normal component towards the surface of the sphere S and cannot be uniquely defined - according to the above-presented Helmholtz theorem – it is required to make use of the condition of Theorem 7 ∇ × Η_Τ = Η_P. In this case the direct operators $-DQ=(r\cdot H_P)$ and $-DP=(r\cdot \nabla \times H_T)$ will bring about the following coinciding inverse $-D^{-1}(r\cdot H_P)$ and $-D^{-1}(r\cdot \nabla \times H_T)=-D^{-1}(r\cdot H_P)$. This means that $P=Q$ and in the expression for A(r) it is sufficient, without loss of generality, to use one arbitrary scalar function, that is, the function $Q$ . So, to find $Q$ , one must define the forward D and inverse D^-1 operators. The inverse operator D^-1 is determined as follows. Let ψ(r, θ, ϕ) and f(r, θ, ϕ) be arbitrary scalar functions, related by:

$D\psi (r,\theta ,\phi )=f(r,\theta ,\phi )$ (56)

In this case, the functions ψ(r, θ, ϕ) and f(r, θ, ϕ) whose mean on S equals zero: $\langle \psi \rangle =0,\langle f\rangle =0$ . Let us introduce the following notation [19, p. 675, paragraph (b)]:

$S_n(\theta ,\phi )={\displaystyle \sum _{m=0}^n{A}_n^m{P}_n^m(cos\theta )e^{im\phi }}$ (57)

where $P_n^m(\cos \theta )$ are the spherical functions, $A_n^m$ are the complex constants $S_n^m(\theta ,\phi )\in C^{\infty }$ . Let us now present the auxiliary functions $\psi ,f$ by their standard extensions in terms of the spherical functions [19]:

$\psi ={\displaystyle \sum _{n=1}^{\infty }{\psi }_n(r)S_n(\theta ,\phi )}={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n{\psi }_n(r)A_n^m{P}_n^m(cos\theta )e^{im\phi }}};f={\displaystyle \sum _{n=1}^{\infty }{f}_n(r){\overline{S}}_n^m(\theta ,\phi ).}$ (58)

The summation over n begins with unit, a free term being absent in accord with the imposed condition of zero means for the functions $Q,\psi ,f$ on the sphere S. In this case, the functions ${\psi }_n(r)$ and $f_n(r)$ are proportional to r ≤ R for rⁿ, while for r ≥ R – to $\frac{1}{r^{n+1}}$ respectively.

Let us apply the direct operator D to the function S_n(θ,ϕ), using the result of (53):

$D{S}_n(\theta ,\phi )=-n(n+1)S_n(\theta ,\phi )$ (59)

In fact, with allowance for (53) and the conditions imposed on the functions ${\psi }_n(r)$ and $f_n(r)$ (58), it is possible to write down:

$-r^2(\frac{{\partial }^2}{\partial r^2}{r}^n{S}_n(\theta ,\phi )+\frac{2}{r}\frac{\partial }{\partial r}{r}^n{S}_n(\theta ,\phi ))=D{r}^n{S}_n(\theta ,\phi );$ From here $-n(n+1)S_n(\theta ,\phi )=D{S}_n(\theta ,\phi ),$ $-r^2(\frac{{\partial }^2}{\partial r^2}\frac{1}{r^{n+1}}{S}_n(\theta ,\phi )+\frac{2}{r}\frac{\partial }{\partial r}\frac{1}{r^{n+1}}{S}_n(\theta ,\phi ))=D\frac{1}{r^{n+1}}{S}_n(\theta ,\phi );$ $-n(n+1)S_n(\theta ,\phi )=D{S}_n(\theta ,\phi ),$

Such a presentation seems to be the most convenient because according to (53) in the operator D the functions are differentiated only with respect to the angular coordinates. Now we apply the operator D to (55) and taking into account the above-obtained extensions of the functions ψ and f, obtain:

$D\psi =-{\displaystyle \sum _{n=1}^{\infty }{\psi }_n(r)n(n+1)S_n(\theta ,\phi )}={\displaystyle \sum _{n=1}^{\infty }{f}_n(r){\overline{S}}_n(\theta ,\phi ).}$ (60)

The functions S_n(θ,ϕ) and differ only in complex coefficients. Let us equate the general terms in (60), keeping in mind the absolute and uniform convergence of a series of extension of the functions ψ,f in the spherical functions [19,20]. Let us now divide the right- and the left-hand sides by the factor n(n + 1). As a result we arrive at:

${\psi }_n(r)S_n(\theta ,\phi )=-f_n(r)\frac{{\overline{S}}_n(\theta ,\phi )}{n(n+1)}.$ (61)

Having summed up all the harmonics in (60), we come to:

$\psi =-D^{-1}f=-{\displaystyle \sum _{n=1}^{\infty }{f}_n(r)\frac{S_n(\theta ,\phi )}{n(n+1)}.}$ (62)

Formula (62) represents the definition of the inverse operator D. In our opinion, the operator in (62) is more constructive for the problem in question than the integral inverse operator for the Beltrami operator containing the Green function [20]. Let us apply it to formulas (55):

$Q=-{\displaystyle \sum _{n=1}^{\infty }r{H}_{Prn}}(r)\frac{{\tilde{S}}_n(\theta ,\phi )}{n(n+1)}=-{\displaystyle \sum _{n=1}^{\infty }r{(\nabla \times H_T)}_{rn}(r)\frac{S_n^{\text{'}}(\theta ,\phi )}{n(n+1)}.}$ (63)

If we take into consideration the fact that for r = R we have H_prn(R) = H_Nn(R),

$H_N(r)={\displaystyle \sum _{n=1}^{\infty }{H}_{Nn}(R)S_n^{\text{'}\text{'}}(\theta ,\phi )},$ $\nabla \times H_T=\nabla \times \nabla \times (Qr)=H_P,$ (64)

then

$Q=-{\displaystyle \sum _{n=1}^{\infty }R{H}_{Nn}(R)\frac{{\tilde{S}}_n(\theta ,\phi )}{n(n+1)}}$ (65)

where R is the radius of the sphere.

Thus, formula (65) defines the function $Q$ on the surface of the sphere. At any of its points inside and outside the sphere, the function $Q$ is known to depend on the coordinate r. Hence, Theorem 7 extends the validity of the Helmholtz theorem by including into a unique definition on the surface of the sphere not only a poloidal magnetic field but also a toroidal magnetic field associated with the poloidal relation from Theorem 7. In order to reconstruct the whole field on the surface S, for Theorem 7 it is required to determine one scalar function on this surface. The toroidal magnetic field is not potential everywhere where, according to definition (6), it is observed. Nevertheless, Theorem 7 allows the reconstruction of the toroidal magnetic field on the surface of the sphere as well. This circumstance is of importance for the interpretation of natural electromagnetic fields observed on the Earth [10].

The Coulomb and the Lorentz calibration conditions for the vector potential presented by a scalar function

One among important problems arising in applications is the problem of the validity of the Coulomb $\nabla \cdot A=0$ or the Lorentz $\nabla \cdot A=\sigma \phi$ calibration when presenting the vector potential by the toroidal orthogonal extension (5). The orthogonality of the vector potential extension from (5) is evident. It is trivially verified in the spherical coordinates:

$\left(0,0,(Qr)\right)\cdot \left({\nabla }_{\theta }\times (Qr),{\nabla }_{\phi }\times (Qr),0\right)\equiv 0$ (66)

Nevertheless, it is still needed to verify the divergence of the vector A in its presentation from (5). This question can be answered by Theorem 8 that was proved in [24].

Theorem 8

The Coulomb $\nabla \cdot A=0$ or the Lorentz $\nabla \cdot A=\sigma \phi$ calibration conditions for the auxiliary vector field A are uniquely fulfilled, if:

$Q(r,\theta ,\phi )=Q(\theta ,\phi )/r^3$ (67)

In fact, from formula (52) follows.

$A=(Qr)+\nabla \times (Qr)+\nabla \phi$ (68)

Let us calculate the divergence from the vector field (68):

$\nabla \cdot A=\nabla \cdot (Qr)+\nabla \cdot \nabla \times (Qr)+\nabla \cdot \nabla \phi$ (69)

In equality (69), the second term by definition equals zero for the rotor divergence. The first term is also equal to zero because of condition (67):

$\nabla \cdot (Qr)=Q\nabla \cdot r+r\nabla Q=\frac{3}{r^3}Q(\theta ,\phi )-\frac{3}{r^3}Q(\theta ,\phi )\equiv 0$ (70)

In the third term, two versions are considered:

$\Delta \phi =\{\begin{array}{l}0\\ \sigma \phi \end{array}$ (71)

where: σ = const.

From formulas (68)-(71) follow two above-mentioned versions of calibrations of the auxiliary vector field A: the Coulomb calibration $\nabla \cdot A=0$ or the Lorentz calibration $\nabla \cdot A=\sigma \phi$ . The theorem has been proved.

Condition (67) from Theorem (8) has a univalent physical essence, which is in that the magnetic fields experimentally decrease as 1/r³. According to the experiment conducted, condition (67) provides a decrease in the non-force magnetic field Η_Τ as well as a decrease in the force magnetic field Η_P.

Generalization of the Gauss and the Schmidt theorems to toroidal and poloidal magnetic fields

The electrodynamics on the Earth dates back to the observations of the magnetic field about five centuries ago in China, when a “magnetic needle” was invented that indicates to the direction and preserves this direction under the action of the magnetic field as it is, whose existence was just a guess. Far more later such a behavior of the “magnetic needle” was employed in navigation [26,27].

The research into the main geomagnetic field (MGF) started in the first half of the 19^th century after publishing the “hitch” studies by Gauss in 1839-1840 [21,22,28]. For the mathematical description of the natural magnetic field, Gauss has offered to use a new (for that time) mathematical object, i.e., a magnetic potential and its decomposition with respect to the sphere. This has formed the basis of the methods for studying the main magnetic field thus formulating principles and approaches to the investigation of the natural magnetic field.

Later the author referred the above works to the static theory of knowledge, to be expressed by:

∇ × Η = 0, Η

At that time, there were no Maxwell’s works on equations of electrodynamics, which appeared only in 1868-1869. Therefore, the question about the nature of the observed magnetic field, i.e. its main property of potentiality, did not arise.

However, in the very beginning of the 20^th century, in 1902 to be exact, Van Vleuten, a physicist from Holland, [28] paid her attention to the fact that the quiet solar-daily variations of the Earth’s magnetism occupy an essential non-potential part in the Earth’s atmosphere. This casted some doubt upon the conventional methodology of studying the main geomagnetic field (MGF) as a potential object in the Earth’s atmosphere. Although due to the absence of the electric current in the non-conducting Earth’s atmosphere, the first Maxwell’s equation ∇ × = j has surely proved the validity of the potential approach for j = 0, ∇ × H = 0. The above methodological principle (static paradigm) is generally accepted even in spite of Benkova’s confirmation of the existence of a non-potential part in the quiet solar-daily variations of the Earth’s magnetism that she has obtained based on the data from the First International Geophysical Year, 1933 [3].

In the very beginning of the 80-s of the 20^th century, Chetaev carried out the experiments in the Earth’s atmosphere with a vertical component of the electric field of short-period variations, which have revealed a sufficiently high stress of this component in the air (1970, [29]). This also contradicted the potentiality principle of variations in the air.

If one attempts to theoretically substantiate the above-considered effects in the Earth’s atmosphere, this will be impossible to implement in the potential paradigm fixed in the Maxwell’s equations. The magnetic field is necessarily potential for j = 0, ∇ × H = 0. The above-described experiments suggest changing this paradigm along with the methodology and approaches to the research into the main geomagnetic field and its variations.

The sources of the new paradigm, which is stationary and uses the formulas:

$\nabla \cdot H=0,H=\nabla \times A,\Delta A=j,\text{ for }t\text{=0, }\Delta A+{\chi }^{2}A=j,\text{ for }t>0$ (73)

can be found in published works on space electrodynamics by Alfven, Parker [5], [18] and in other related works.

The most important discovery is a theoretical proof of a possible existence of the non-force toroidal magnetic fields, whose properties, as was shown above, differ from those fixed in the first Maxwell’s equation. Changing the potential property for a more general solenoidal one, originating from the equation: $\nabla \cdot H=0$ , makes possible to introduce the natural geomagnetism into the new paradigm, which is stationary, and to replace the existing methodology of studying the MGF by a more general one. The substantiation of the new paradigm is based on a number of theorems published in mathematical, physical and geophysical journals [10,12,24,31].

The new approach, in our opinion, must be based on the conviction that the Earth is just the same cosmic object as all the other planets and stars surrounding it. Its magnetic field in its origin cannot strongly differ from the existing ways of generation of the cosmic bodies magnetic fields. This idea is repeatedly emphasized by Parker [5]. Moreover, the principle of dynamo excitation of a magnetic field is sometimes transferred to the Earth’s conditions, although by now there has been no its experimental confirmation in the Earth’s conditions [30].

The experiment on a cosmic object, i.e. the Earth, was carried out three times: two experiments during the International Geophysical Years of 1933 and 1957-1958, and the third one – during the world-wide magnetic surveying in 1964-1965.

In this connection, the problem of interpreting the observed fields requires the development of a maximally general theory of appearance of the electromagnetic fields observed on the Earth with allowance for the Earth’s cosmic nature and the above effects observed on the Earth’s surface. To this end, there was a need in creating the new electrodynamics, which would originate from Maxwell’s equations and as a minimum, equations of the space electrodynamics. Above, such an electrodynamics has been created (36).

Based on the conclusions of the new electrodynamics it is necessary to develop an effective theory for interpreting the data observed in the course of the international geophysical years of 1933 and 1957/1958 and the world-wide magnetometer survey of 1964/1965 with allowance for a possible existence of non-force magnetic fields. In this case it is needed to bear up against the well-known and well-substantiated Gauss-Schmidt method [21,23], applied to investigation of natural magnetic fields in the static statement. With this method, a number of problems have been solved by means of extending the magnetic potential in terms of the sphere and using experimental data determining in it unknown constants. The coincidence with the experiment has simultaneously helped to solve two problems: the existence of a solution and its uniqueness. The problem of stability was solved with the help of the method of least squares, developed by Gauss for approximation of observed data. Therefore it seems reasonable to use this method as the basis when interpreting the data containing non-force electromagnetic fields. The method in question, as was noted above, solves the problem of existence, uniqueness and stability of the problem solution of reproduction of the electromagnetic field on a sphere by discrete observational data. In addition, the Gauss-Schmidt method makes possible to solve rather a complicated problem of detecting the location of sources of the reproduced magnetic field. These can be sources inside the sphere and outside it.

Therefore it is necessary to begin the simulation of the magnetic field of sources inside the sphere and outside it with modern presentation of the Gauss-Schmidt theory [10].

Let in the sphere W with the boundary $S\text{(}\overline{W}=W\text{U}S\text{)}$ there be located magnetic masses with the density ρ_m. Then equations for the potential magnetic field H inside the sphere can be written down in the form:

$\nabla \times H=0,\nabla \cdot H={\rho }_m$ (74)

Formulas (74) generate the following chain of equalities:

$H=\nabla V,\nabla \cdot \nabla V=\Delta V={\rho }_m$ (75)

Here: V is the scalar function of the class C∞.

The solution to the Poisson equation (75) in the sphere will be the integral:

$V={\displaystyle \underset{W}{\int }\frac{{\rho }_m(p)}{r(p,q)}d{w}^{\prime }}$ (76)

where p is the point inside the sphere, q is the point outside the sphere.

The inverse radius in (76) 1/r(p,q) can be presented by the Gauss hypergeometric series [28] or with the help of the Legendre spherical functions [20], for example,

$\begin{array}{l}1/r(p,q)={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[{\overline{c}}_n^m\cos m\phi \cos m{\phi }^{\prime }{P}_n^m(\cos \theta )}}{P}_n^m(\cos {\theta }^{\prime })+\\ +{\overline{c}}_n^m\sin m\phi \sin m{\phi }^{\prime }{P}_n^m(\cos \theta )P_n^m(\cos {\theta }^{\prime })]\frac{{r^{\prime }}^n}{r^{n+1}},\end{array}$ $r\le R$ (77)

p>Where R is radius of the sphere, ${\overline{c}}_n^m$ is the number of combinations n with respect to m, $p(r^{\prime },{\theta }^{\prime },{\phi }^{\prime }),q(r,\theta ,\phi )$ are the coordinates of points in the spherical coordinate system, fixed at the center of the sphere, $P_n^m(\cos \theta )$ are the adjoined Legendre functions.

The summation over n in (77) begins with unity according to the assumption that the mean of the function V∈ C∞ through the sphere S is equal to zero:

$\langle V\rangle ={\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{\pi }{\int }}V\sin \theta d\theta d\phi =0}}$ (78)

Substituting (77) into (76) yields:

$\begin{array}{l}V={\displaystyle \sum _{n=1}^{\infty }\frac{1}{r^{n+1}}{\displaystyle \sum _{m=0}^n[\cos m\phi P_n^m(\cos \theta ){\overline{c}}_n^m{\displaystyle \underset{W}{\int }{\rho }_m(p){r^{\prime }}^n\cos m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{w}^{\prime }+}}}+\sin m\phi P_n^m(\cos \theta ){\overline{c}}_n^m{\displaystyle \underset{W}{\int }{\rho }_m(p){r^{\prime }}^n\sin m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{w}^{\prime }]}\\ +\sin m\phi P_n^m(\cos \theta ){\overline{c}}_n^m{\displaystyle \underset{W}{\int }{\rho }_m(p){r^{\prime }}^n\sin m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{w}^{\prime }]}\end{array}$ (79)

Then, assuming the density of magnetic masses ${\rho }_m(r^{\prime },{\theta }^{\prime },{\phi }^{\prime })$ to by a complex function of coordinates inside the sphere, the integrals in (79) can be denoted by the complex constants $A_n^m$ and $B_n^m$ , thus providing the completeness of the decomposition of the potential V in terms of the spherical functions:

$\begin{array}{l}{A}_n^m={\overline{c}}_n^m{\displaystyle \underset{W}{\int }{\rho }_m(p)}{r^{\prime }}^n\cos m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{w}^{\prime }\\ B_n^m={\overline{c}}_n^m{\displaystyle \underset{W}{\int }{\rho }_m(p)}{r^{\prime }}^n\sin m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{w}^{\prime }\end{array}$ (80)

In this case, extension (79) takes the form:

$V={\displaystyle \sum _{n=1}^{\infty }\frac{1}{r^{n+1}}{\displaystyle \sum _{m=0}^n(A_n^m\cos m\phi +B_n^m\sin m\phi )}}{P}_n^m(\cos \theta )$ (81)

Let us introduce into (81) the following notation:

$A_n^m=R^{n+2}{g}_n^m,B_n^m=R^{n+2}{h}_n^m$ (82)

Extension (81) with allowance for (82) will look like

$V=R{\displaystyle \sum _{n=1}^{\infty }{(\frac{R}{r})}^{n+1}{\displaystyle \sum _{m=0}^n(g_n^m\cos m\phi +h_n^m\sin m\phi )}}{P}_n^m(\cos \theta )$ (83)

The potential in (83) on the surface of the sphere for r = R will take the form:

$V=R{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(g_n^m\cos m\phi +h_n^m\sin m\phi )}}{P}_n^m(\cos \theta )$ (84)

According to (75), the magnetic field components in the local coordinate system fixed on the sphere S, where x is the direction opposite to that of the coordinate θ, zis the direction inward the sphere, y is the direction coinciding with that of the coordinate φ, with allowance for (75) and (83) can be calculated:

$\begin{array}{l}{H}_x^i=-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(g_n^m\cos m\phi +h_n^m\sin m\phi )}}\frac{\partial P_n^m(\cos \theta )}{\partial \theta },\\ H_y^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(g_n^m\sin m\phi -h_n^m\cos m\phi )}}\frac{m{P}_n^m(\cos \theta )}{\sin \theta },\\ H_z^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(g_n^m\cos m\phi +h_n^m\sin m\phi )}}(n+1)P_n^m(\cos \theta )\text{ (85)}\end{array}$

Formulas (84) have conceptually completed the result, obtained in the Gauss theorem [28] about the extension (reconstruction) of the magnetic potential using the data on the sphere S. With the magnetic field components (85) as an addition to the result obtained by Gauss it is possible to reconstruct (decompose) the potential magnetic field on the sphere S by means of one scalar function V.

It is easy to note that formulas (85) also correspond to the Helmholtz theorem of uniqueness [19]. According to (85) for reconstructing the whole magnetic field it is sufficient to have on the surface S the regular (or sparse in approximation theory) data on the vertical component of the magnetic field Η_Z. With these data, it is possible to reconstruct the coefficients $g_n^m$ and $h_n^m$ that will be sufficient for reconstructing all the three components of the magnetic field from (85).

Much later the Gauss theorem was supplemented by Schmidt [23] under the assumption that magnetic masses take place also outside the sphere. In this case, it is necessary to decompose the inverse radius from (77) in terms of the following functions:

$\begin{array}{l}1/r(p,q)={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[{\overline{c}}_n^m\cos m\phi \cos m{\phi }^{\prime }{P}_n^m(\cos \theta )}}{P}_n^m(\cos {\theta }^{\prime })+\\ +{\overline{c}}_n^m\sin m\phi \sin m{\phi }^{\prime }{P}_n^m(\cos \theta )P_n^m(\cos {\theta }^{\prime })]\frac{r^n}{{r^{\prime }}^{n+1}}r\ge R\end{array}$ (86)

Substituting (86) into integral (76) and bearing in mind that the masses outside the sphere in the volume $\overline{W}$ with the complex density ${\overline{\rho }}_m(r,\theta ,\phi )$ , obtain:

$\begin{array}{l}\overline{V}={\displaystyle \sum _{n=1}^{\infty }{r}^n{\displaystyle \sum _{m=0}^n[\cos m\phi P_n^m(\cos \theta ){\overline{c}}_n^m{\displaystyle \underset{W}{\int }\frac{1}{{r^{\prime }}^{n+1}}{\overline{\rho }}_m(q)\cos m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{w}^{\prime }+}}}\\ +\sin m\phi P_n^m(\cos \theta ){\overline{c}}_n^m{\displaystyle \underset{W}{\int }\frac{1}{{r^{\prime }}^{n+1}}{\overline{\rho }}_m(q)\sin m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{w}^{\prime }]}\end{array}$ (87)

In (87), we introduce the notation:

$C_n^m={\displaystyle \underset{\overline{W}}{\int }\frac{{\overline{c}}_n^m{\overline{\rho }}_m(q)}{{r^{\prime }}^{n+1}}}\cos m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{\overline{w}}^{\prime },D_n^m={\displaystyle \underset{\overline{W}}{\int }\frac{{\overline{c}}_n^m{\overline{\rho }}_m(q)}{{r^{\prime }}^{n+1}}}\sin m{\phi }^{\prime }{P}_n^m(\cos {\theta }^{\prime })d{\overline{w}}^{\prime }$ (88)

Then, once again, we denote:

$c_n^m=R^{(n-1)}{C}_n^m,d_n^m=R^{(n-1)}{D}_n^m$ (89)

and obtain the expressions for the magnetic potential of the masses outside the sphere W.

$\overline{V}={\displaystyle \sum _{n=1}^{\infty }\frac{r^n}{R^{n-1}}{\displaystyle \sum _{m=0}^n(c_n^m\cos m\phi +d_n^m\sin m\phi )P_n^m(\cos \theta )}}$ (90)

On the surface of the sphere, the magnetic potential of masses outside it, for r = R we can write down:

$\overline{V}=R{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(c_n^m\cos m\phi +d_n^m\sin m\phi )P_n^m(\cos \theta )}}$ (91)

The magnetic field components in the local coordinate system x, y, z will be the following:

$\begin{array}{l}{H}_x^e=-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(c_n^m\cos m\phi +d_n^m\sin m\phi )}}\frac{\partial P_n^m(\cos \theta )}{\partial \theta },\\ H_y^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(c_n^m\sin m\phi -d_n^m\cos m\phi )\frac{m{P}_n^m(\cos \theta )}{\sin \theta }}},\\ H_z^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(c_n^m\cos m\phi +d_n^m\sin m\phi )}}n{P}_n^m(\cos \theta )\end{array}$ (92)

Summing up (85) and (92) in the local coordinate system and introducing the following notation:

$\begin{array}{l}\{\begin{array}{l}{g}_n^m+c_n^m=a_n^m,\\ (n+1)g_n^m-n{c}_n^m={\overline{a}}_n^m,\end{array},\\ \{\begin{array}{l}{h}_n^m+d_n^m=b_n^m,\\ (n+1)h_n^m-n{d}_n^m={\overline{b}}_n^m,\end{array}\end{array}$ (93)

we obtain the pairs of equations whose determinant is equal to –(2n + 1), which ensures the uniqueness of separation of coefficients of magnetic fields into the coefficients of magnetic fields from the inner (inside the sphere) and outer (outside the sphere) magnetic masses.

The resulting extension of the summarized magnetic field on the surface S of the sphere W are written down as follows:

$\begin{array}{l}{H}_x=-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(a_n^m\cos m\phi +b_n^m\sin m\phi )\frac{\partial P_n^m(\cos \theta )}{\partial \theta }}},\\ H_y={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(a_n^m\sin m\phi -b_n^m\cos m\phi )}}\frac{m{P}_n^m(\cos \theta )}{\sin \theta },\\ H_z={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n({\overline{a}}_n^m\cos m\phi +{\overline{b}}_n^m\sin m\phi )}}{P}_n^m(\cos \theta )\end{array}$ (94)

Formulas (94) conclude the Gauss-Schmidt theory on decomposition (reconstruction) of the magnetic field from the internal and external sources, i.e. magnetic masses, relative to the surface S [28,33].

In (94), unknown are the complex coefficients $a_n^m,b_n^m,{\overline{a}}_n^m,{\overline{b}}_n^m,$ that can be found from the data on the surface S both at separate points (for approximation theory) and over the whole sphere in the form, for example, of magnetic maps available for the experts in Geomagnetism.

It should also be noted that for the complete separation (reconstruction) by formulas (93) and (94) of magnetic fields into the fields from the internal in the sphere $\overline{W}$ and external in the domain W sources, it is sufficient to have data on the vertical component of the field Η_Z and one of tangential components Η_x or Η_y on the surface S. This proves the following theorem.

Theorem 9

For interpolation and complete separation (reconstruction) of magnetic fields of magnetic masses in the sphere W from the magnetic fields of magnetic masses outside the sphere (in the domain $\overline{W}$ ) the data about the two components of the magnetic field are sufficient: the vertical and one of tangential components to the surface S (an analog to the Gauss-Schmidt theorems).

Formulas (94) complete the development of the first (static) formalism based on the assumption of potentiality of the constant magnetic field everywhere as related to the previous assumption about a source of a magnetic field as magnetic masses.

The static paradigm in the form of formulas (92) and (94) is considered to be applicable to the case when the sphere W and the domain $\overline{W}$ are scattered and in them constant non-divergent electric currents are circulating [27]. To do this, it is necessary to simulate closed electric currents in sources with magnetic sheets, and to measure magnetic fields in the no-current region between W and $\overline{W}$ [27]. Such a situation as if is observable in the Earth’s atmosphere when studying its constant magnetic field and its long-period variations observed in the atmosphere by the world network of stations or obtained as a result of the worldwide magnetic survey of 1964/1965.

However in the latter case when applying decompositions (94), their insufficiently precise interpolation properties were noticed [27]. As was elucidated [10, 31,32] this is associated with penetration into the Earth’s atmosphere of non-potential (by definition) toroidal magnetic fields from the spherical sources: non-divergent electric currents or the currents on the spherical surfaces, for example, in the ionosphere (the sources of the Earth’s long-period magnetic field variations).

In the penetration of a non-potential magnetic field to the Earth’s non-conducting atmosphere, the Gauss-Schmidt theorem (Theorem 9) on separation of static magnetic fields can be re-formulated and proved for a stationary case as well.

Теорема 9.1.

The problem of separation of poloidal and toroidal vector fields of the sources located outside the sphere V from the same fields but from the sources located inside the sphere is uniquely solved if the external normal component H_N(r) and one of the two tangential components H_t(r)) of the summarized vector field H on the surface S of the sphere V are known.

In fact, let on S, according to formula (65), the summarized scalar function $Q=Q^e+Q^i$ , which consists of the outer part $Q^e$ and the inner part $Q^i$ , be known. Taking into account formulas (58) and (65), it is possible on the surface S to write down the following:

$Q^e+Q^i=-{\displaystyle \sum _{n=1}^{\infty }R\frac{S_n(\theta ,\phi )}{n(n+1)}}[A_n\frac{1}{R^{n+1}}+B_n{R}^n],$ (94.1)

where A_n and B_n are complex constants to the outer A_n and the inner B_n function $Q$ . The toroidal and poloidal components of the magnetic field on the surface of the sphere S are calculated using definitions (6) and (7):

$\begin{array}{l}{H}_T=\frac{1}{\sin \theta }\frac{\partial }{\partial \phi }(Q^e+Q^i)e_{\theta }-\frac{\partial }{\partial \theta }(Q^e+Q^i)e_{\phi },\\ H_P=\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial }{\partial \theta }(Q^e+Q^i)e_{\theta }+\frac{1}{r\sin \theta }\frac{\partial }{\partial r}r\frac{\partial }{\partial \phi }(Q^e+Q^i)e_{\phi }-\\ -\frac{1}{r\sin \theta }\left(\frac{\partial }{\partial \theta }\sin \theta \frac{\partial }{\partial \theta }(Q^e+Q^i)-\frac{1}{\sin \theta }\frac{{\partial }^2}{\partial {\phi }^2}(Q^e+Q^i)\right)e_r.\end{array}$ (94.2)

Keeping in mind the dependence of the function Q on radius r for external and internal sources in terms of (67) and omitting trivial formulas, we write down the poloidal field components in the following way:

$\begin{array}{l}{H}_{P\theta }=-\frac{n}{r^{n+2}}\frac{\partial }{\partial \theta }{Q}^e+(n+1)r^{n-1}\frac{\partial }{\partial \theta }{Q}^i,\\ H_{P\phi }=-\frac{n}{r^{n+2}}\frac{1}{\sin \theta }\frac{\partial }{\partial \phi }{Q}^e+(n+1)r^{n-1}\frac{1}{\sin \theta }\frac{\partial }{\partial \phi }{Q}^i,\\ H_{Pr}=\frac{1}{r\sin \theta }\left[\cos \theta \frac{\partial (Q^e+Q^i)}{\partial \theta }+\sin \theta \frac{{\partial }^2(Q^e+Q^i)}{\partial {\theta }^2}-\frac{1}{\sin \theta }\frac{{\partial }^2(Q^e+Q^i)}{\partial {\phi }^2}\right]\end{array}$ (94.3)

Based on formulas (94.2), (94.3) and (65) we present the tangential components of the summarized magnetic field and its normal component in the form:

$\begin{array}{l}{H}_{t\theta }=-{\displaystyle \sum _{n=1}^{\infty }{X}_n(\theta ,\phi )}\frac{1}{n(n+1)}\left[-A_n\frac{n}{R^{n+1}}+B_n(n+1)R^n\right],\\ H_{t\phi }=-{\displaystyle \sum _{n=1}^{\infty }{Y}_n(\theta ,\phi )\frac{1}{n(n+1)}\left[-A_n\frac{n}{R^{n+1}}+B_n(n+1)R^n\right]},\\ H_N={\displaystyle \sum _{n=1}^{\infty }{Z}_n(\theta ,\phi )}\frac{1}{n(n+1)}\left[A_n\frac{1}{R^{n+1}}+B_n{R}^n\right].\end{array}$ (94.4)

Here $X_n(\theta ,\phi ),Y_n(\theta ,\phi ),Z_n(\theta ,\phi )\in C^{\infty }$ are complex angular functions that are derivatives of the known function S_n(θ,φ). Formulas (94.4) indicate to the fact that any pair consisting of one tangential and one normal component makes possible to uniquely separate coefficients of the external and internal vector fields with respect to the surface S since the determinant of separating equations differs from zero:

$\left|\begin{array}{l}\frac{1}{R^{n+1}},R^n\\ -\frac{n}{R^{n+1}},{\text{ (n+1)R}}^n\end{array}\right|=\frac{(2n+1)}{R}.$ (94.5)

The separate calculation of $Q^e$ and $Q^i$ allows the reconstruction on the surface of the sphere S of the poloidal and toroidal vector fields both from the sources inside the sphere and from the outer sources. According to the data on the MGF for 1965, the numerical implementation of the separation algorithm with allowance for the toroidal fields is presented in [10].

The concept of Theorem 9, as one might expect, spreads to the solenoidal magnetic fields containing both the toroidal and poloidal parts.

The author has developed an efficient algorithm, mainly, for the sparse data on the sphere based on the stationary paradigm and equation (36). This algorithm is based on the following formulas:

$\nabla \times H=j,\nabla \cdot H=0$ (95)

Here: j is the density of non-divergent electric currents in the sphere W or in the domain $\overline{W}$ .

As is easy to see in (95), the magnetic field inside the sphere W and outside it in the domain $\overline{W}$ is non-potential, and an auxiliary function, i.e. the vector potential, is introduced reasoning from the solenoid property of the magnetic field with the help of the following chain of equalities

$H=\nabla \times A,\nabla \times \nabla \times A=j,\nabla \nabla \cdot A-\Delta A=j,\nabla \cdot A=0,\Delta A=-j$ (96)

The following integral is the solution to the latter equation in (96) in the sphere W:

$A={\displaystyle \underset{W}{\int }\frac{j(p)}{r(p,q)}d{w}^{\prime }}$ (97)

where j(p) is the current density in the sphere W.

The further use of integral (97) with minor changes is similar to that above-mentioned. First, it is necessary to take into account the vector property of the current density j(p) and its complex dependence on the coordinates of the point p.

Second, it is possible to uniquely write down the vector potential as components coinciding with those of the current density j(p) in the integrand function in the rectangular coordinate system fixed at the center of the sphere. Then:

$A_x={\displaystyle \underset{W}{\int }\frac{j_x(p)}{r(p,q)}d{w}^{\prime },A_y={\displaystyle \underset{W}{\int }\frac{j_y(p)}{r(p,q)}}}d{w}^{\prime },A_z={\displaystyle \underset{W}{\int }\frac{j_z(p)}{r(p,q)}d{w}^{\prime }}$ (98)

Then the components of potential (98) must be expressed in the spherical components in order to make use of the inverse radius decomposition in integrals (98) in terms of the spherical functions, according to (77) and (86):

$\begin{array}{l}{A}_{\theta }=A_x\cos \theta \cos \phi +A_y\cos \theta \sin \phi -A_z\sin \theta ,\\ A_{\phi }=-A_x\sin \phi +A_y\cos \phi ,\\ A_z=A_x\sin \theta \cos \phi +A_y\sin \theta \sin \phi +A_z\cos \theta .\end{array}$ (99)

Substituting expansions (77) into integrals (98) and omitting intermediate formulas (similar to the above ones) we write down the spherical components of the vector potential from the sources with the complex density of the currents inside the sphere:

$\begin{array}{l}{A}_{\theta }^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[({\ae }_n^{m}cosm\phi +{\rho }_n^{m}sinm\phi )cos\theta cos\phi +}}\\ +({\mu }_n^{m}cosm\phi +{\nu }_n^{m}sinm\phi )cos\theta sin\phi -\\ -(u_n^{m}cosm\phi +v_n^{m}sinm\phi )sin\theta ]\frac{R^{n+2}}{r^{n+1}}{P}_n^m(cos\theta ),\\ A_{\phi }^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[-({\text{æ}}_n^{m}cosm\phi +{\rho }_n^{m}sinm\phi )sin\phi +}}r\ge R\text{ (100)}\\ +({\mu }_n^{m}cosm\phi +{\nu }_n^{m}sinm\phi )cos\phi ]\frac{R^{n+2}}{r^{n+1}}{P}_n^m(cos\theta ),\\ A_r^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[({\text{æ}}_n^{m}cosm\phi +{\rho }_n^{m}sinm\phi )sin\theta cos\phi +}}\\ +({\mu }_n^{m}cosm\phi +{\nu }_n^{m}sinm\phi )sin\theta sin\phi +\\ +(u_n^{m}cosm\phi +v_n^{m}sinm\phi )cos\theta ]\frac{R^{n+2}}{r^{n+1}}{P}_n^m(cos\theta ).\end{array}$

In formulas (100), the decomposition coefficients have the following physical sense. First, these are integrals of the current density components of the form:

${\text{æ}}_n^m=\frac{1}{R^{n+2}}{\displaystyle \underset{W}{\int }{r^{\prime }}^n{j^{\prime }}_x(p)cosm{\phi }^{\prime }{P}_n^m(cos{\theta }^{\prime })}d{w}^{\prime }$ , ${\rho }_n^m=\frac{1}{R^{n+2}}{\displaystyle \underset{W}{\int }{r^{\prime }}^n{j^{\prime }}_x(p)sinm{\phi }^{\prime }{P}_n^m(cos{\theta }^{\prime })d{w}^{\prime }}$ , ${\mu }_n^m=\frac{1}{R^{n+2}}{\displaystyle \underset{W}{\int }{r^{\prime }}^n{j^{\prime }}_y(p)cosm{\phi }^{\prime }{P}_n^m(cos{\theta }^{\prime })}d{w}^{\prime }$ , (101) ${\nu }_n^m=\frac{1}{R^{n+2}}{\displaystyle \underset{W}{\int }{r^{\prime }}^n{j^{\prime }}_y(p)sinm{\phi }^{\prime }{P}_n^m(cos{\theta }^{\prime })}d{w}^{\prime }$ , $u_n^m=\frac{1}{R^{n+2}}{\displaystyle \underset{W}{\int }{r^{\prime }}^n{j^{\prime }}_z(p)cosm{\phi }^{\prime }{P}_n^m(cos{\theta }^{\prime })}d{w}^{\prime }$ , $v_n^m=\frac{1}{R^{n+2}}{\displaystyle \underset{W}{\int }{r^{\prime }}^n{j^{\prime }}_z(p)sinm{\phi }^{\prime }{P}_n^m(cos{\theta }^{\prime })}d{w}^{\prime }$ .

Second, it is known hat the expression $r^{\prime }\cos {\theta }^{\prime }$ is the projection of the radius of the vector $r^{\prime }$ on the axis $z^{\prime }$ , and the expression $r^{\prime }\sin {\phi }^{\prime }\sin {\theta }^{\prime }$ is its projection on the axis $y^{\prime }$ , etc. In this connection, the constant complex coefficients in (101) in the first approximation can be written down as follows, for example:

${\text{æ}}_1^0=\frac{1}{R^3}{\displaystyle \underset{W}{\int }{z}^{\prime }{j}_x(p)d{w}^{\prime }=\frac{{M^{\prime }}_y}{R^3}},{\rho }_1^1=\frac{1}{R^3}{\displaystyle \underset{W}{\int }{y}^{\prime }}{j}_x(p)d{w}^{\prime }=-\frac{{M^{\prime }}_z}{R^3}$ , etc. (102)

From (102) it follows that the complex coefficients represent the projections of moments of different orders of an a rbitrary current system on an axis of the rectangular coordinate system, the component j_x(p) giving only the projections $M_{n{y}^{\prime }}^m\text{ and }{M}_{n{z}^{\prime }}^m$ , while the component j_y(p) generates only the projections $M_{n{x}^{\prime }}^m\text{ and }{M}_{n{z}^{\prime }}^m$ , etc. These facts are significant for solving problems not only of interpolation of sparse data on the sphere S but also for physical applications [10,31,32].

If the sources of the magnetic field are located outside the ball W, namely in the region $\overline{W}$ , the components of the vector potential will take the form:

$\begin{array}{l}{A}_{\theta }^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[(a_n^{m}cosm\phi +b_n^{m}sinm\phi )cos\theta cos\phi +}}(c_n^{m}cosm\phi +d_n^{m}sinm\phi )cos\theta sin\phi -\\ (e_n^{m}cosm\phi +f_n^{m}sinm\phi )sin\theta ]\frac{r^n}{R^{n-1}}{P}_n^m(cos\theta ),\\ A_{\phi }^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[-(a_n^{m}cosm\phi +b_n^{m}sinm\phi )}}sin\phi +,\\ (c_n^{m}cosm\phi +d_n^{m}sinm\phi )cos\phi ]\frac{r^n}{R^{n-1}}{P}_n^m(cos\theta ),\\ A_r^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[(a_n^{m}cosm\phi +b_n^{m}sinm\phi )sin\theta cos\phi +}},\\ (c_n^{m}cosm\phi +d_n^{m}sinm\phi )sin\theta sin\phi +,\\ (e_n^{m}cosm\phi +f_n^{m}sinm\phi )cos\theta ]\frac{r^n}{R^{n-1}}{P}_n^m(cos\theta )\end{array}$ $r\le R+h\text{ (103)}$

where h is the distance between the sphere W and the domain $\overline{W}$ .

$H_x=-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[-{\overline{i}}_n^{m}msinm\phi cos\phi +{\overline{j}}_n^{m}mcosm\phi cos\phi }}$, ${\overline{k}}_n^{m}msinm\phi sin\phi +{\overline{l}}_n^{m}mcosm\phi sin\phi ]P_n^m(cos\theta )-$ , $({\overline{q}}_n^{m}sinm\phi -{\overline{p}}_n^{m}cosm\phi )mctg\theta P_n^m(cos\theta )+$ , $[-{\tilde{i}}_n^{m}cosm\phi sin\phi -{\tilde{j}}_n^{m}sinm\phi sin\phi +{\tilde{k}}_n^{m}cosm\phi cos\phi +$ , ${\tilde{l}}_n^{m}sinm\phi cos\phi ]P_n^m(cos\theta ),$ , $H_y=-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[{\overline{i}}_n^{m}cosm\phi cos\phi +{\overline{j}}_n^{m}sinm\phi cos\phi +}}$ , ${\overline{k}}_n^{m}cosm\phi sin\phi +{\overline{l}}_n^{m}sinm\phi sin\phi ]sin\theta \frac{\partial P_n^m(cos\theta )}{\partial \theta }+$ , (104) $({\overline{q}}_n^{m}cosm\phi +{\overline{p}}_n^{m}sinm\phi )cos\theta \frac{\partial P_n^m(cos\theta )}{\partial \theta }+$ , $[{\tilde{i}}_n^{m}cosm\phi cos\phi +{\tilde{j}}_n^{m}sinm\phi cos\phi +{\tilde{k}}_n^{m}cosm\phi sin\phi +$ , $[{\tilde{i}}_n^{m}cosm\phi cos\phi +{\tilde{j}}_n^{m}sinm\phi cos\phi +{\tilde{k}}_n^{m}cosm\phi sin\phi +$ , $\begin{array}{l}{\tilde{l}}_n^{m}sinm\phi sin\phi ]cos\theta P_n^m(cos\theta )+\\ ({\tilde{q}}_n^{m}cosm\phi +{\tilde{p}}_n^{m}sinm\phi )sin\theta P_n^m(cos\theta ),\end{array}$ , $H_z={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n{\overline{i}}_n^m\left(cosm\phi sin\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }-msinm\phi cos\phi ctg\theta P_n^m(cos\theta )\right)+}}$ , ${\overline{j}}_n^m\left(sinm\phi sin\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }+mcosm\phi cos\phi ctg\theta P_n^m(cos\theta )\right)-$ , ${\overline{k}}_n^m\left(cosm\phi cos\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }+msinm\phi sin\phi ctg\theta P_n^m(cos\theta )\right)-$ , ${\overline{l}}_n^m\left(sinm\phi cos\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }-mcosm\phi sin\phi ctg\theta P_n^m(cos\theta )\right)+$ , ${\overline{q}}_n^{m}msinm\phi P_n^m(cos\theta )-{\overline{p}}_n^{m}mcosm\phi P_n^m(cos\theta ).$

The analysis of formulas (104) indicates to a more complicated character of the interpolation formulas for the decomposition (reconstruction) of magnetic components on the surface of the sphere S as related to (94). For finding all complex coefficients in extension (104), it is sufficient to have data on the surface of the sphere S. It is easy to see that in forming interpolation formulas with three scalar components of the vector potential of arbitrary electric currents (except for dipole) it is sufficient to have data only on the local component H_y including the whole set of unknown complex constants. In this sense, vector sources, namely, non-divergent electric currents in the sphere W and outside the domain $\overline{W}$ in their summarized magnetic field require the measurement of one horizontal component H_y for the complete separation and reconstruction of the whole field. In this case, the separating equations are of the form:

$\{\begin{array}{l}{\text{æ}}_n^m+a_n^m={\overline{i}}_n^m,\\ (n+1){\text{æ}}_n^m-n{a}_n^m={\tilde{i}}_n^m;\end{array}\{\begin{array}{l}{\rho }_n^m+b_n^m={\overline{j}}_n^m,\\ (n+1){\rho }_n^m-n{b}_n^m={\tilde{j}}_n^m;\end{array}$ , $\{\begin{array}{l}{\mu }_n^m+c_n^m={\overline{k}}_n^m,\\ (n+1){\mu }_n^m-n{c}_n^m={\tilde{k}}_n^m;\end{array}\{\begin{array}{l}{\nu }_n^m+d_n^m={\overline{l}}_n^m,\\ (n+1){\nu }_n^m-n{d}_n^m={\tilde{l}}_n^m;\end{array}$ , $\{\begin{array}{l}{u}_n^m+e_n^m={\overline{q}}_n^m,\\ -(n+1)u_n^m+n{e}_n^m={\tilde{q}}_n^m;\end{array}\{\begin{array}{l}{v}_n^m+f_n^m={\overline{p}}_n^m,\\ -(n+1)v_n^m+n{f}_n^m={\tilde{p}}_n^m.\end{array}$ (105)

The determinants in (105) are equal to ±(2_n + 1), thus providing the uniqueness of separation of coefficients from other ones.

Theorem 10

For interpolation and complete separation (reconstruction) of magnetic fields of arbitrary non-divergent electric currents in the sphere from the magnetic fields of non-divergent electric currents in the domain outside, it is sufficient to have data about one component of the magnetic field Η_y that is tangential to the surface of the sphere.

Thus, in the complete magnetic field, the solution to the problem of separation of coefficients in terms of (104) and (105) minimizes up to one component the requirement of the Gauss and the Schmidt theorems (Theorem 9) containing two such components.

The author has comprehensively investigated the numerical properties of interpolation formulas (104) [10,32]. These properties have revealed essential advantages of formulas (104) as compared to (94) when interpreting sparse data of the worldwide network of magnetic surveys [10].

These results have covered the second formalism when developing interpolation formulas for separation (reconstruction) of magnetic fields based on the data about the surface of the sphere S.

It is easy to see that in the second formalism there is no need to predetermine the potentiality of the magnetic field in the area between the sphere W and the domain $\overline{W}$ . The algorithm has been developed owing to the principle of solenoid features of the magnetic field in the absence of data on the configuration of currents in the space domains they occupy. In the algorithms developed, only the non-divergence of electric currents is clearly present. Therefore in the second formalism due to its high accuracy it appeared possible to verify the indirect indications to the fact that when magnetic fields are generated by non-divergent toroidal currents in the sphere W and in the domain $\overline{W}$ , there may occur non-potential magnetic fields in the area between W and $\overline{W}$ [2,3]. From the standpoint of standard Maxwell’s equations, represented by formulas (74) and (95), the appearance of a non-potential field in the area without currents between W and $\overline{W}$ is impossible. Really, according to the Stokes theorem:

${\displaystyle \underset{L}{\int }(H\cdot dl)={\displaystyle \underset{\overline{S}}{\int }(\nabla \times H\cdot ds)={\displaystyle \underset{\overline{S}}{\int }{j}_n\cdot ds|{}_{j_n=0}=0}}}$ (106)

Nevertheless, the verification of (106) with the help of a magnetic field measured in the Earth’s atmosphere yields a result drastically different from (106). A non-potential magnetic field is almost half the magnetic field of quiet solar-daily variations with the absence of the electric current through the atmosphere [2,3,10].

Further it is needed to formulate the third formalism developed for studying the problem of magnetic fields from the non-divergent toroidal electric currents in the sphere W and outside it in the domain $\overline{W}$ . To this end, according to (5), it is necessary to make use of the first formula from (96) and the non-standard orthogonal toroidal decomposition of the vector potential A:

$A=(Q\cdot r)+\nabla \times (Q\cdot r)$ (107)

where $Q$ is the scalar function of the three variables (r, θ, φ) of the class C∞, r is the radius-vector. Decomposition (107) makes possible to uniquely introduce the toroidal and poloidal magnetic fields from the toroidal electric currents investigated in [6].

$H_T=\nabla \times (Qr),H_P=\nabla \times \nabla \times (Qr),$, $\nabla \times H_T=\nabla \times \nabla \times (Qr)=H_P,\nabla \times H_P=\nabla \times \nabla \times \nabla \times (Qr)=\chi H_T,$ (108)

where $\chi =\frac{\gamma }{\eta },\gamma$ is the rate of the magnetic field diffusion, $\eta =\frac{1}{\sigma \mu }$ is the magnetic viscosity, σ is the conductivity in the sphere W or $\overline{W}$ , µ is the magnetic permeability in them. Formulas (96) and (107) allow one to express the vector potential components by means of one scalar function in the following form:

$A_{\theta }=\frac{1}{\sin \theta }\frac{\partial Q}{\partial \phi },A_{\phi }=-\frac{\partial Q}{\partial \theta },A_r=rQ,$ (109)

and a magnetic field of the poloidal and toroidal types, respectively, by the formulas:

$\begin{array}{l}{H}_{P\theta }=\frac{1}{r}\frac{\partial }{\partial r}\frac{\partial }{\partial \theta }(Qr)=-\frac{1}{r}\frac{\partial }{\partial r}r{A}_{\phi },H_{P\phi }=\frac{1}{r}\frac{\partial }{\partial r}\frac{1}{sin\theta }\frac{\partial }{\partial \phi }(Qr)=\frac{1}{r}\frac{\partial }{\partial r}r{A}_{\theta },\\ H_{Pr}=-\frac{1}{r^{2}sin\theta }\left(\frac{\partial }{\partial \theta }sin\theta \frac{\partial (Qr)}{\partial \theta }+\frac{\partial }{\partial \phi }\frac{1}{sin\theta }\frac{\partial (Qr)}{\partial \phi }\right)=\\ -\frac{1}{rsin\theta }\left(-\frac{\partial }{\partial \theta }sin\theta A_{\phi }+\frac{\partial }{\partial \phi }{A}_{\theta }\right).\\ H_{T\theta }=\frac{1}{rsin\theta }\frac{\partial }{\partial \phi }(Qr)=\frac{1}{rsin\theta }\frac{\partial }{\partial \phi }{A}_r,H_{T\phi }=-\frac{1}{r}\frac{\partial }{\partial \theta }(Qr)=-\frac{1}{r}\frac{\partial }{\partial \theta }{A}_r.\end{array}$ (110)

Taking formulas (110) into account it is possible to write on the surface of the sphere S the expressions for the poloidal and toroidal magnetic fields from the sources located inside the sphere W:

$H_{P\theta }^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[-n{\text{æ}}_n^{m}cosm\phi sin\phi -n{\rho }_n^{m}sinm\phi sin\phi +}}n{\mu }_n^{m}cosm\phi cos\phi +n{\nu }_n^{m}sinm\phi cos\phi ]P_n^m(cos\theta ),$, $H_{P\phi }^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[-n{\text{æ}}_n^{m}cosm\phi cos\phi cos\theta -n{\rho }_n^{m}sinm\phi cos\phi cos\theta -}}n{\mu }_n^{m}cosm\phi sin\phi cos\theta -n{\nu }_n^{m}sinm\phi sin\phi cos\theta +$ , $n{u}_n^{m}cosm\phi sin\theta +n{v}_n^{m}sinm\phi sin\theta ]P_n^m(cos\theta ),$ , $H_{Pr}^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n{\text{æ}}_n^m\left(cosm\phi sin\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }-msinm\phi cos\phi ctg\theta P_n^m(cosm\phi )\right)}}+$ , ${\rho }_n^m\left(sinm\phi sin\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }+mcosm\phi cos\phi ctg\theta P_n^m(cos\theta )\right)-$ , ${\mu }_n^m\left(cosm\phi cos\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }+msinm\phi sin\phi ctg\theta P_n^m(cos\theta )\right)-$ , ${\nu }_n^m\left(sinm\phi cos\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }-mcosm\phi sin\phi ctg\theta P_n^m(cos\theta )\right)+$ , $\left(u_n^{m}sinm\phi -v_n^{m}cosm\phi \right)m{P}_n^m(cos\theta ).$ , $H_{T\theta }^i={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[-{\text{æ}}_n^m(cosm\phi sinm\phi +msinm\phi cos\phi )+}}\text{ (111)}$ , ${\rho }_n^m(mcosm\phi cos\phi -sinm\phi sin\phi )+{\mu }_n^m(cosm\phi cos\phi -msinm\phi sin\phi )+$ , ${\nu }_n^m(mcosm\phi sin\phi +sinm\phi cos\phi )+(-u_n^{m}sinm\phi +v_n^{m}cosm\phi )mctg\theta ]P_n^m(cos\theta ),$ , $H_{T\phi }^i=-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n\left({\text{æ}}_n^{m}cosm\phi cos\phi +{\rho }_n^{m}sinm\phi cos\phi )(cos\theta P_n^m(cos\theta )+sin\theta \frac{\partial P_n^m(cos\theta )}{\partial \theta }\right)}}+$ , $({\mu }_n^{m}cosm\phi sin\phi +{\nu }_n^{m}sinm\phi sin\phi )\left(cos\theta P_n^m(cos\theta )+sin\theta \frac{\partial P_n^m(cos\theta )}{\partial \theta }\right)+$ , $(u_n^{m}cosm\phi +v_n^{m}sinm\phi )\left(cos\theta \frac{\partial P_n^m(cos\theta )}{\partial \theta }-sin\theta P_n^m(cos\theta )\right).$

Formulas (111) show that for reconstructing the whole magnetic field including its toroidal part from the sources inside the sphere, it is sufficient to possess data only about the vertical to the surface S component of the poloidal field $H_{\mathrm{Pr}}^i=H_z$ (Η_Z in the local coordinate system). This is in agreement with Theorems 5, 7. Theorem 5 generalizes the Helmholtz theorem [19] about the unique decomposition (reconstruction) of the whole poloidal and toroidal magnetic field in terms of its normal component on the sphere S.

A similar situation arises when it is required to obtain decompositions for a poloidal and a toroidal magnetic field S from external sources of the domains $\overline{W}$ as well as on the spherical surface S. Having omitted intermediate formulas, obtain:

$H_{P\theta }^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[(n+1)a_n^{m}cosm\phi sin\phi +(n+1)b_n^{m}sinm\phi sin\phi -}}(n+1)c_n^{m}cosm\phi cos\phi -(n+1)d_n^{m}sinm\phi cos\phi ]P_n^m(cos\theta ),$, $H_{P\phi }^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[((n+1)a_n^{m}cosm\phi cos\phi +(n+1)b_n^{m}sinm\phi cos\phi +}}(n+1)c_n^{m}cosm\phi sin\phi +(n+1)d_n^{m}sinm\phi sin\phi )cos\theta -$ , $((n+1)e_n^{m}cosm\phi +(n+1)f_n^{m}sinm\phi )sin\theta ]P_n^m(cos\theta ),$ , $H_{Pr}^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n{a}_n^m\left(cosm\phi sin\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }-msinm\phi cos\phi ctg\theta P_n^m(cos\theta )\right)+}}$ , $b_n^m\left(sinm\phi sin\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }+mcosm\phi cos\phi ctg\theta P_n^m(cos\theta )\right)-$ , $c_n^m\left(cosm\phi cos\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }+msinm\phi sin\phi ctg\theta P_n^m(cos\theta )\right)-$ , $d_n^m\left(sinm\phi cos\phi \frac{\partial P_n^m(cos\theta )}{\partial \theta }-mcosm\phi sin\phi ctg\theta P_n^m(cos\theta )\right)+$ , $(e_n^{m}sinm\phi -f_n^{m}cosm\phi )m{P}_n^m(cos\theta ).\text{ (112)}$ , $H_{T\theta }^e={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n[-a_n^m(cosm\phi sin\phi +msinm\phi cos\phi )+}}{b}_n^m(-sinm\phi sin\phi +mcosm\phi cos\phi )+$ , $c_n^m(cosm\phi cos\phi -msinm\phi sin\phi )+d_n^m(sinm\phi cos\phi +mcosm\phi sin\phi )+$ , $(-e_n^{m}sinm\phi +f_n^{m}cosm\phi )mctg\theta ]P_n^m(cos\theta ),$ , $H_{T\phi }^e=-{\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{m=0}^n(a_n^{m}cosm\phi +b_n^{m}sinm\phi )cos\phi \left(cos\theta P_n^m(cos\theta )+sin\theta \frac{\partial P_n^m(cos\theta )}{\partial \theta }\right)}}+$ , $(c_n^{m}cosm\phi +d_n^{m}sinm\phi )sin\phi \left(cos\theta P_n^m(cos\theta )+sin\theta \frac{\partial P_n^m(cos\theta )}{\partial \theta }\right)+$ , $(e_n^{m}cosm\phi +f_n^{m}sinm\phi )\left(-sin\theta P_n^m(cos\theta )+\cos \theta \frac{\partial P_n^m(cos\theta )}{\partial \theta }\right).$,

If expressions (111) and (112) are summed up, it appears possible to obtain formulas (104) in the Cartesian coordinate system x, y, z as well. As is clear, formulas (104) are in agreement with Theorem 10. On the other hand, if unknown coefficients are obtained by means of (104), then, according to (105), by their separation it appears possible to separately calculate the poloidal and toroidal fields from internal and external sources not only on the surface S, but also at any other points including those between W and $\overline{W}$ .

Theorem 11

For reconstructing the whole magnetic field, including its toroidal part from the sources inside the sphere, it is sufficient to have “continuous” (or “rarefied” in approximate theory) data about the normal to the component S of the poloidal magnetic field H_pr (An analogue to the Helmholtz Theorem 6).

It should be noted that the third formalism proposed by the author made possible to positively answer the main question whether the toroidal currents (non-divergent currents j(p) in the sphere are able to generate a non-potential toroidal magnetic field outside this sphere in the non-conducting domain between W and $\overline{W}$ , to be exact. According to definitions (108), the answer is definitely positive. This resolves the problem of the presence of a non-potential part of the Earth’s magnetic field, for example, in the atmosphere [2,3]. This non-potential part is associated not with a potential toroidal magnetic field, whose vortices everywhere generate a poloidal field but not the electric current, which would arise according to standard Maxwell’s equations. A non-potential magnetic field is present in the Earth’s atmosphere, while there is practically no electric current. This is due to the presence there of a non-potential toroidal magnetic field.

Thus, studying the electrodynamics of magnetic field sources as magnetic masses and closed electric currents inside and outside a sphere has shown a drastic all difference between the electrodynamics of magnetic masses at the expense of appearance everywhere in the magnetic field of electric currents and its non-potential toroidal part. Its appearance is due to the spherical property of the source, i.e. the electric current in the sphere W and in the domain $\overline{W}$ . The influence of the spherical property of electric currents is studied in considerable detail in [10,32].

The convergence of all the above-discussed decompositions of magnetic fields in terms of spherical functions, as is mentioned in [20], is not worse than that of Fourier series, because these extensions are finally expressed through combinations of trigonometric functions.