More Information
Submitted: 18 February 2020 | Approved: 14 July 2020 | Published: 15 July 2020
How to cite this article: Hossain I, Abdullah HY. Ground-state bands of doubly even 166Hf Nucleus. Int J Phys Res Appl. 2020; 3: 115-117.
DOI: 10.29328/journal.ijpra.1001027
ORCiD: orcid.org/0000-0002-0840-6983
Copyright License: © 2020 Hossain I, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Ground state; Rotational bands; Semi-empirical formula; 166Hf
Ground-state bands of doubly even 166Hf Nucleus
I Hossain1* and Hewa Y Abdullah2
1Department of Physics, Rabigh College of Science and Arts, King Abdulaziz University, Post Box 344, Rabigh 21911, Saudi Arabia
2Physics Education Department, Faculty of Education, Tishk International University, Erbil, Iraq
*Address for Correspondence: Mohammad Hossain, Department of Physics, Rabigh College of Science and Arts, King Abdulaziz University, Post Box 344, Rabigh 21911, Saudi Arabia, Tel: +966-558141319; Email: [email protected]; [email protected]
This study was carried out to investigate the rotational structure of even-even 166Hf isotopes using the phenomenological fitting, Sood’s semi-empirical formula. The rotational energies from the calculated values were compared to the experimental spectrum. The result shows that in 166Hf, calculated energies fit the experimental values to a remarkable degree of accuracy.
In the collective model proposed by Bohr and Mottelson [1], a new parameter called nuclear deformation is introduced, in which the surface of the nucleus may undergo oscillations in a rotating nucleus. These results in the prediction of rotational energy levels being restricted to even values due to oscillating symmetry, and it is easily observed with nuclei having a number of nucleons far from closed shells. Experimental data comes to a good agreement with these predictions, and applications such as probability for B (E2) transitions, magnetic moments, quadruple moments and isomeric transitions are so far successful.
In the macroscopic view, the common simplest starting point of modeling the atomic nucleus is based on semi-classical liquid drop model [2,3] where the nucleus is assumed to behave a drop of dense incompressible liquid where the spherical shape is the result of attractive forces between all the particles contained in the nucleus. This model is then expanded to describe quantum mechanical collective motion, such as rotation and vibrations, leading to the Bohr and Mottelson collective model [1]. In the collective model, a new parameter called nuclear deformation is introduced, in which the surface of the nucleus may undergo oscillations in a rotating nucleus. These results in the prediction of rotational energy levels being restricted to even values due to oscillating symmetry, and it is easily observed with nuclei having a number of nucleons far from closed shells. In current study, we contribute the ground state bands of rotational spectra of even-even Hafnium 166Hf nucleus with spin state up to 18+ by the phenomenological fitting of Sood’s semi-empirical formula (SSEF).
Theoretical calculations
The shape of atomic nuclei with a large number of nucleons outside of closed shells is axially symmetric and permanently deformed [1]. The rotational energy spectrum of such an axially symmetric rotator shows the characteristic J(J+1) dependence if we take adiabatic approximations for the motions of all the particles in the nucleus. The low-lying energy levels follows spin sequence Jπ = 0+, 2+, 4+, 6+, ... , for all of even parity rotational nuclei with each energy level given by the expression [4]:
EJ = AJ(J+1) (1)
Where rotational parameter A is inversely proportional to the nuclear moment of inertia ℑ, such that A = ħ2/2ℑ. The moment of inertia is also assumed to be constant following an approximation where the energy ratio E (4+)/E (2+) = 10/3, E (6+)/E (2+) = 7, E (8+)/E (2+) = 12. Deviations by a few percent from these ratios are thought to be a coupling of vibrational and rotational modes of the nuclei. This coupling depends on J2 and constitutes changes in rotational energy from the first-order perturbation theory. However, for fitting the first three or four excited states, the first-order correction term can be added to equation (1) where the rotational energy [4-6]:
EJ = AJ(J + 1) – BJ2(J + 1)2 (2)
Stephens, et al. [7] and Singh, et al. [8] added second-order CJ3(J+1)3 and third-order DJ4(J+1)4 correction terms respectively to account the deviations in energy bands for even-even actinide nuclei. The rotational energy equation according to an infinite power series as [9].
EJ = AJ(J + 1) – BJ2(J + 1)2 + CJ3(J + 1)3 – DJ4(J + 1)4 (3)
Assuming that the coefficient parameters are constant through each successive order of correction terms, where C/B = D/C = N (B/A) Sood derived a semi-empirical formulation for rotational energy by summing of infinite series in equation (3):
(4)
Where ratio B/A = (10-3R)/ (200-18R) and R = E (4+) /E (2+). The constant N was obtained by Sood [9] via empirical method was:
N = 2.85 – 0.05J
In this study, Sood’s semi-empirical formula (SSEF) has been utilized to calculate the ground state bands of even-even hafnium nucleus of A = 166 with spin state up to 18+. Hafnium nucleus was chosen because it lies at the beginning of the transition region between well deformed rare-earth nuclei and the doubly-closed spherical 208Pb nucleus [10].
The calculated values of energy levels based on Sood’s semi-empirical formula are presented with experimental values of low-lying rotational energy levels where Kπ = 0+ and Jπ take even values from 0+ up to 18+. We note that the percentage of deviation between calculated and experimental values is very small. The discrepancy increases in higher spin states of even-even 166Hf nucleus.
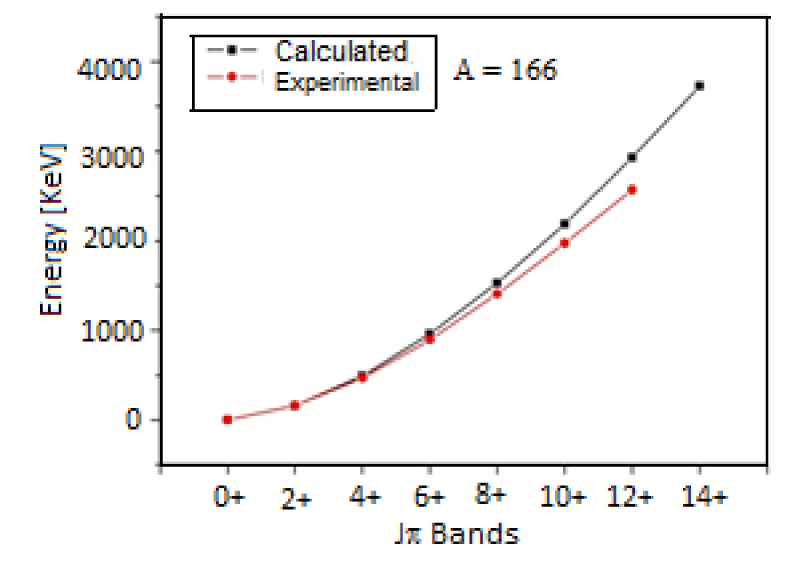
To ease the presentation of data, numerical results extracted from nuclear data sheets are presented as red dots in a graph of the spin state against excitation energy in the KeV scale. The black squares represent calculated energy values based on Sood’s semi-empirical formula. The purpose of lines connecting the points is only to guide the eyes because the spin state takes integer values. The error bars in experimental values are not visible due to relatively small values compared to observed energy scales.
From figure 1, we notice that for Hafnium isotopes with mass number 166, the phenomenological Sood’s semi-empirical formula fits the observed energies to the extent of remarkable agreement up to spin state 18+ which relate to data in table 1. However, in higher spin states, deviations are observed between calculated and experimental energies. For 166Hf, the deviation is 0.52, 5.05, 6.94, 8.76, 11.05 and 14.08% at 2+, 4+, 6+, 8+, 10+, 12+ and 14+ states respectively. The deviations from J(J+1) rule in rotational energy bands are interpreted as the compression of energy levels, or in other words, an increase in nuclear moment of inertia as the nucleus undergoes changing rotational angular velocity. The calculated results fit the experimental values to a remarkable degree of accuracy. The results of our calculation for 166Hf show good agreement with data in comparison with other calculation [9].
Figure 1: Ground state rotational bands of even-even 166Hf nucleus.
| Table 1. The experimental and theoretical calculation of ground-state bands of 166Hf nucleus. The deviations between experimental and calculated values are presented in percentage. | |||
| A = 166 [11] | |||
| Jπ | Experiment | Calculation | Deviation |
| keV | keV | % | |
| 0+ | 0 | 0 | 0 |
| 2+ | 158.64(5) | 159.468 | 0.52 |
| 4+ | 470.46(6) | 494.221 | 5.05 |
| 6+ | 897.17(12) | 959.461 | 6.94 |
| 8+ | 1406.4(6) | 1529.588 | 8.76 |
| 10+ | 1971.9(6) | 2189.879 | 11.05 |
| 12+ | 2565.8(7) | 2927.08 | 14.08 |
| 14+ | − | 3725.367 | − |
| 16+ | − | 4564.833 | − |
| 18+ | − | 5420.566 | − |
Sood’s semi-empirical formula is successfully applied to calculate the rotational spectrum of even-even 166Hf isotopes. The results align well with experimental values within the expectations of the simple phenomenological fitting. The calculated data, as well as experimental data, indicated that 166Hf nucleus is rotational spectrum. The deviations from J(J+1) rule in rotational energy bands are interpreted as the compression of energy levels.
- Bohr A, Mottelson BR. Collective and Individual-Particle Aspects of Nuclear Structure. Kgl Danske Videnskab. Selskab Mat-fys. Medd. 1953; 27: 1-174.
- Feenberg E. Semi-empirical Theory of the Nuclear Energy Surface. Revs Mod Phys. 1947; 19: 233.
- Green ES, Engler NA. Mass Surfaces. Phys Rev.1953; 91: 40.
- Preston MA, Bhaduri RA. Structure of the Nucleus. Addison-Wesley Publishing Company. 1975.
- Saethre O, Hjorth SA, Johnson A, Jägare S, Ryde H, et al. Angular Velocity Expansions of Nuclear Rotational Energies. Nucl Phys A. 1973; 207: 486-512.
- Johnson A, Szymański Z. Nuclear Rotation at High Angular Velocities. Physics Reports C Phys Lett. 1973; 7: 181-222.
- Stephens FS Jr, Diamond RM, Perlman I, Phys Rev Lett. 1959; 3: 435.
- Singh K, Sahota HS. Study of Rotational States in Even-Even Nuclei in the Energy Region A ≥ 228. Ind J Phys. 1985; 59: 57.
- Sood PC. Comparative Study of Two Parameter Models for Predicting Rotational Energies in Even-Even Nuclei. Nuclear Data A. 1968; 4: 281-300.
- Kumar A, Gunye MR. The Yrast States of The Even Hafnium Isotopes 166-172Hf. J Phys G Nucl Phys. 1980; 6: 229 – 240.
- Baglin M, Nucl Data Sheets for A = 166, Nucl Dat Sheets. 2008; 109: 1103-1382.