More Information
Submitted: March 05, 2021 | Approved: April 03, 2021 | Published: April 05, 2021
How to cite this article: Skumiel A. Influence of high frequency rotating magnetic field on the effect of heating magnetic fluid. Int J Phys Res Appl. 2021; 4: 015-018.
DOI: 10.29328/journal.ijpra.1001035
Copyright License: © 2021 Skumiel A. This is an open access article distributed under the Creative Commons Attribution License, which peRmits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Influence of high frequency rotating magnetic field on the effect of heating magnetic fluid
Andrzej Skumiel*
Faculty of Physics, Adam Mickiewicz University, Uniwersytetu Poznańskiego 2, 61-614 Poznań, Poland
*Address for Correspondence: Andrzej Skumiel, Faculty of Physics, Adam Mickiewicz University, Uniwersytetu Poznańskiego 2, 61-614 Poznań, Poland, Email: [email protected]
The article describes the necessary conditions for the phenomenon of thermal energy release in a magnetic fluid placed in a high-frequency rotating magnetic field. The minimum amplitude of the magnetic field was calculated and the thermal power released (by the rotating spherical nanoparticles in the viscous medium) was estimated. The estimations were based on the assumption that the magnetic relaxation times (τN and τB) and the magnetic field rotation period (τrot) meet the condition: τN>>τrot>>τB. The principle of operation and construction of the device generating a high-frequency rotating magnetic field is described. Preliminary experimental studies were carried out using a magnetic fluid with magnetite nanoparticles that indicated magnetic relaxation as the cause of the released heat. The value of the absorption rate in the experiment and its dependence on the strength of the magnetic field were determined.
Currently, magnetic fluids (MF) are studied both from the experimental and theoretical side [1,2] due to their unique physical properties and wide application. Computer simulations [1,2] of the flows of these media through micro-channels are used in theoretical models, their instability and heat flow phenomena are investigated [3]. Magnetic liquids containing magnetic nanoparticles (NPs) are susceptible to being controlled [4] by external electric and magnetic fields.
For years magnetic nanoparticles have been increasingly used in many fields of technology and in biomedicine. They are used in biomedicine in magnetic resonance imaging, drug delivery or in magnetic hyperthermia (MH). The action of MH is to achieve a local increase of temperature in target cells by local activation of magnetic nanoparticles under the influence of alternating high-frequency magnetic field.
Placing magnetic nanoparticles in a variable high-frequency magnetic field causes a thermal effect. The reason for this phenomenon is to release thermal energy in the magnetic fluid. When NPs are small particles and have only superparamagnetic properties, the main reason for the thermal effect is magnetic relaxation. The phenomenon of magnetic relaxation has been explained by the Néel mechanism and by the Brownian mechanism. Both these magnetization mechanisms occur with characteristic relaxation times(τN, τB) depending on the size of the magnetic core τm and the hydrodynamic diameter dh, as well as the properties of the magnetic material of the grain, liquid viscosity ηS and temperature T [5]. Depending on the value of these parameters, the mechanism with a smaller relaxation time dominates. When τN>>τB, Néel’s mechanism is negligible, and this case concerns nanoparticles with slightly larger sizes. Then the rotation of the magnetization vector inside the magnetic core is practically blocked and the entire nanoparticle rotates. This means that such a particle can rotate in a rotating magnetic field (RMF), as long as the driving torque is greater than the resistance of the liquid medium.
Among the methods, the use of an oscillating magnetic field [6,7] is widespread, but recently there have been reports describing the RMF [8,9]. Because the oscillating magnetic field is relatively easy to generate (even at high frequencies), it is most often used for heating up MF. However, an RMF can yield a higher heat output [8] than an oscillating field at the same values of magnetic field amplitude and frequency. If a NP is placed in a RMF [10], it can rotate in this viscous medium and due to the friction, thermal energy is released and its temperature rises. Thus, two moments of forces act simultaneously on the nanoparticle: the driving torque Td and the torque τb from resistance forces surrounding the medium.
Mechanical driving torque Td resulting from the action of the external magnetic field on the magnetic moment MS·Vm of the NP is defined as [11]:
(1)
where, H - is the intensity of magnetic field, Vm – volume of the magnetic core, µ0 = 4π·10-7 H·m-1 is the permeability of vacuum, MS is the saturation magnetization of the magnetic material and θ is angle between vectors H and magnetic moment.
If the sphere rotates in a viscous fluid with frequency f - without slipping relative to the RMf - the braking torque τb acts on it equals [12].
(2)
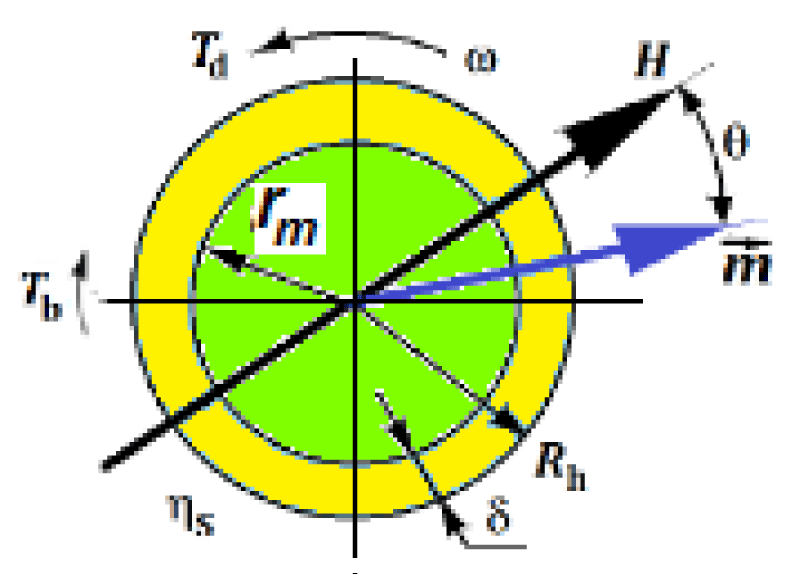
where dh is hydrodynamic diameter and ηS is viscosity coefficientof fluid. This situation is shown in figure 1 during the magnetic spherical NP is immersed in a viscous liquid.
Figure 1: The action of moments of driving Td and braking force τb on a magnetic NP immersed in a viscous fluid in a RMF.
The operation of these two torques leads to a rotation of the spherical nanoparticles when the following condition is fulfilled: Td > τb. When the additional condition τrot > τeff is fulfilled, then both magnetization mechanis MS (Néel and Brown) take part in heat release effect, where τrot is the period of field rotation, τeff is the effective relaxation time.
In practice, several cases of the experiment can be observed by selecting the magnetic fluid of the appropriate NPs size and magnetic field frequency, such as:
1). τN>τrot>τB, where Néel mechanism is eliminated,
2). τB>τrot>τN, where Brown mechanism is eliminated,
3). τrot>τN = τB, where both magnetization mechanisms take an equal part in MF heating.
From the comparison of the driving moment Td and the braking moment τb, we obtain the expression (3) for the minimum magnetic field strength H:
(3)
required during NP rotation without slipping relative to field rotation. This expression implies that a low required magnetic field value will be if MF has a low viscosity value and a low surfactant layer thickness.
Construction and parameters of magnetic circuits
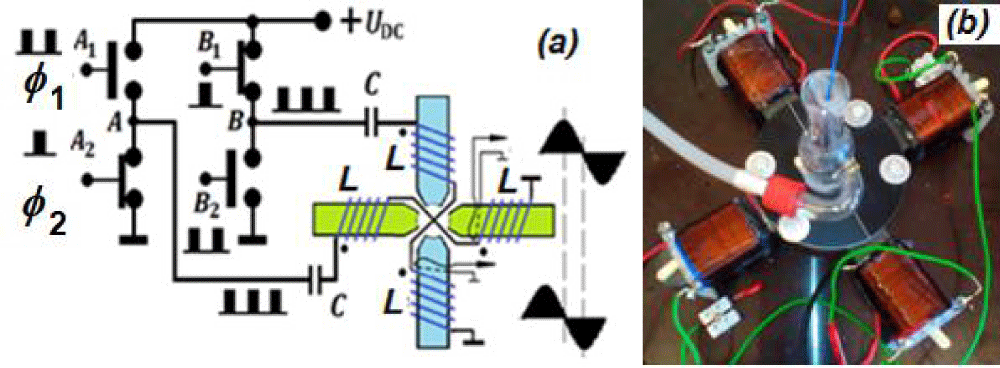
In order to create a RMF, the author developed a measuring system (Figure 2a) consisting of two LC branches whose axes were spaced in every 900 degrees of angularity, and the electrical signals fed to them had phase shift of 900 degrees. The system used 2-channel function generators SIGLENT TECHNOLOGIES SDG1025 in which the frequency and phase were set independently in each channel. The generator’s signals from both channels controlled electronic keys. The coils were wound on ferrite cores Ferroxube I100/25/25 and the inductance of each branch was L = 1.8 mH. The HVCA capacitor with an electrical capacity of C = 8 nF was connected in series with each branch. The minimum impedance of each such branch occurred at the resonance frequency f = 41.9 kHz. Figure 2b shows the view of magnetic circuits with Liebieg cooler, which was connected to a temperature stabilization system.
Figure 2: System configuration for generating a rotating magnetic field with two LC branches (a) and view of magnetic circuits with Liebieg cooler (b).
In experiments, the optical fiber temperature sensor [13] by FISO Technology Inc., model FOT-L-SD was used with temperature range (−40 ÷ 300)°C, with response time better than 1.5 s, accuracy of 0.10°C and resolution of 0.01°C.
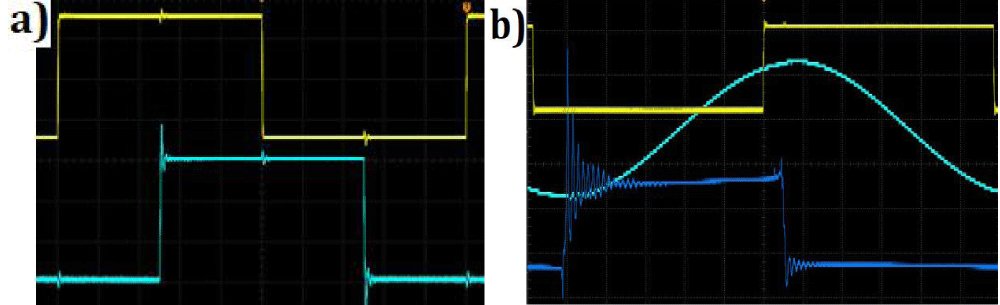
The voltage signal on the branches has a rectangular shape but due to the selective properties of the LC circuit, the currents flowing through the coils (also magnetic streaMS) have a sinusoidal waveform, as shown in figure 3. The visible sinusoidal voltage wave induced on one turn loop additional wound on a ferrite core corresponds to the basic distribution component of the Fourier series. Other, higher components of the series are eliminated by a bandpass filter with LC branch.
Figure 3: Time courses of signals controlling switches mutually shifted in phase by 90 angular degrees (a), Time signal wave for MS: synchronizing (upper, yellow), rectangular on the LC branch (lower, blue) and sinusoidal on one turn wound on the ferrite core (middle, aquamarine) (b).
Calorimetric tests in a RMF were made in an liquid based on transformer oil with magnetite (Fe3O4) NPs coated with oleic acid. The sizes of the magnetite particles were determined using a TEM microscope and are shown in figure 4. Additional physical parameters of NPs and MF are summarized in table 1.
Figure 4: TEM images of magnetite particles.
| Table 1: Physical properties of nanoparticles and magnetic fluid. | |
| Physical parameters | Symbols and their values |
| Material | magnetite Fe3O4 |
| magnetic diameter | <dm> = 11.8 nm |
| hydrodynamic diameter | <dh> = 15.8 nm |
| viscosity coefficient of carrier liquid | ηs@ 9.7 mNs·m-2 at T=298K |
| magnetic saturation of magnetite NPs | MS = 446 A·m-1 |
| specific heat capacity of the MF sample | cS = 1.54J·g-1·K-1 |
| density of the MF sample | mS = 0.9498 g·cm-3 |
| mass of the magnetite in 1 ml | mNP=143mg |
| parameters from Eq.(4) | a = 79495 and n = 1.95 |
| SLP at H=4 kA·m-1 & f = 41.9 kHz | SLP= 52 mW·g-1 |
| the relaxation time according to the Néel mechanism | tN = 10 ns |
| the relaxation time according to the Brown mechanism | tB = 15 ms |
From the magnetization curve, the volume concentration of magnetite particles, ϕV = 2.76% was obtained. The results of fitting the log-normal function describing the distribution of NPs provided the following size values: the mean diameters <d> = 11.8 nm and the mean standard deviation <σ> = 5.0 nm. Considering the frequency of magnetic field (f = 41.9 kHz), nanoparticle sizes (τm ≅ 11.8 nm, dh ≅ 15.8 nm), carrier liquid parameters (ηS ≅ 9.7 mNs·m-2) and temperature (T = 298K), the relation between the period of magnetic field rotation in relation to the magnetic relaxation times in experiment was as follows: τrot>τB>>τN.
It follows that both mechanisms were involved in the release of heat. However, mainly the Néel’s mechanism dominated: (τrot = 24 µs) > (τB = 15 µs) >>(τN = 10 ns).
Results of calorimetric experiments and analysis
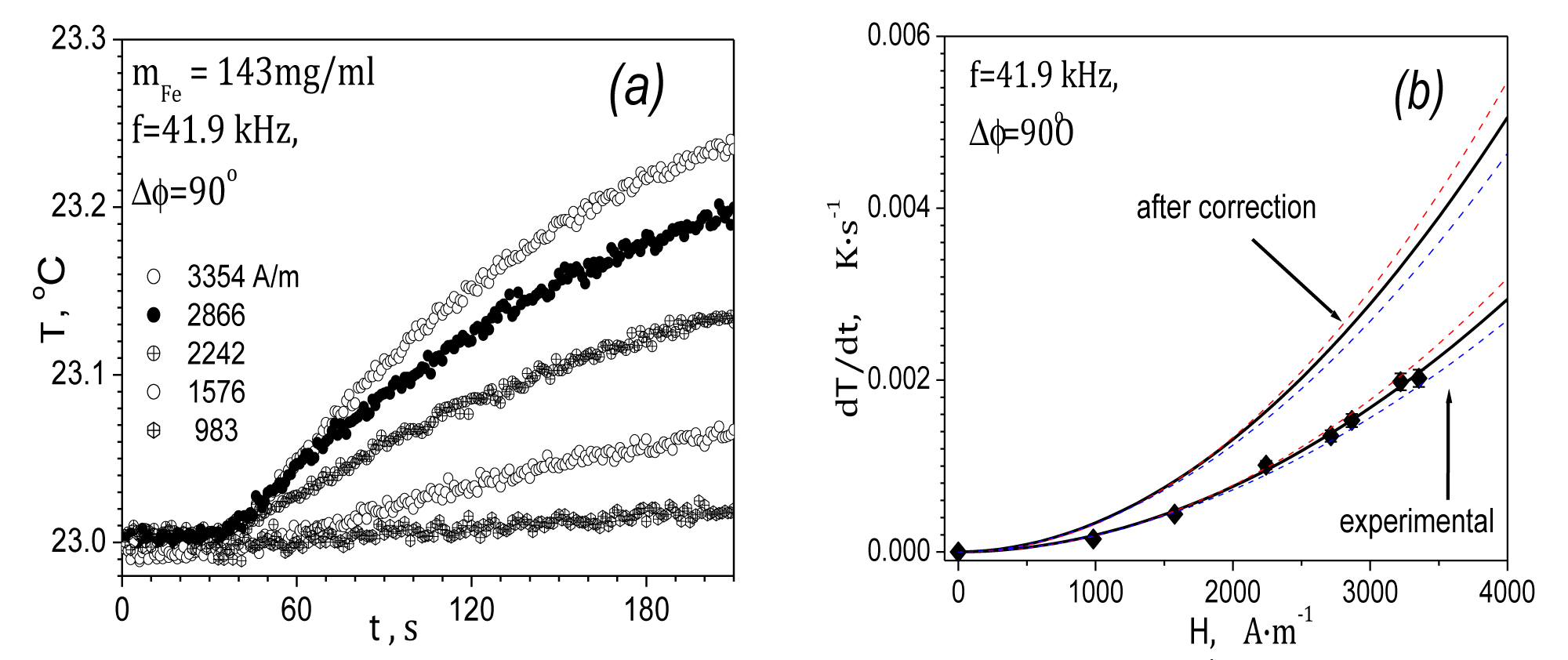
The result of the magnetic heating experiment in the RMF is presented in figure 5a for selected values of magnetic field strength amplitude. The dependence of the temperature increase rate (dT/dt)t = 0 [10] determined by the formula (4) as a function of the amplitude of the magnetic field intensity [14] is shown in figure 5b.
Figure 5: Time courses of the temperature during heating (a) and dependence of (dT/dTt)t=0 on the RMF strength amplitude in studied sample (b).
(4)
where a = 79495 and n = 1.95 are parameters obtained from matching equation (4) to experimental data. Dotted lines show the error range resulting from matching the function to experimental data. An additional reason for the measurement error is related to the dissipation of thermal energy from the MF to the glass vial. Because the mass of MF is less than glass vial mass, the heating effect [9] should be corrected and Tcor = 1.72·Texp.
In order to evaluate the efficiency of the heating process of the MF under the influence of the external magnetic field, the specific loss power (SLP) was determined by the formula [15]:
(5)
where cS =1.54 J·g-1·K-1 is the specific heat capacity of the sample, MS = 0.9498g·cm-3 and mNP = 143 mg/ml are the density of MF and magnetic material respectively.
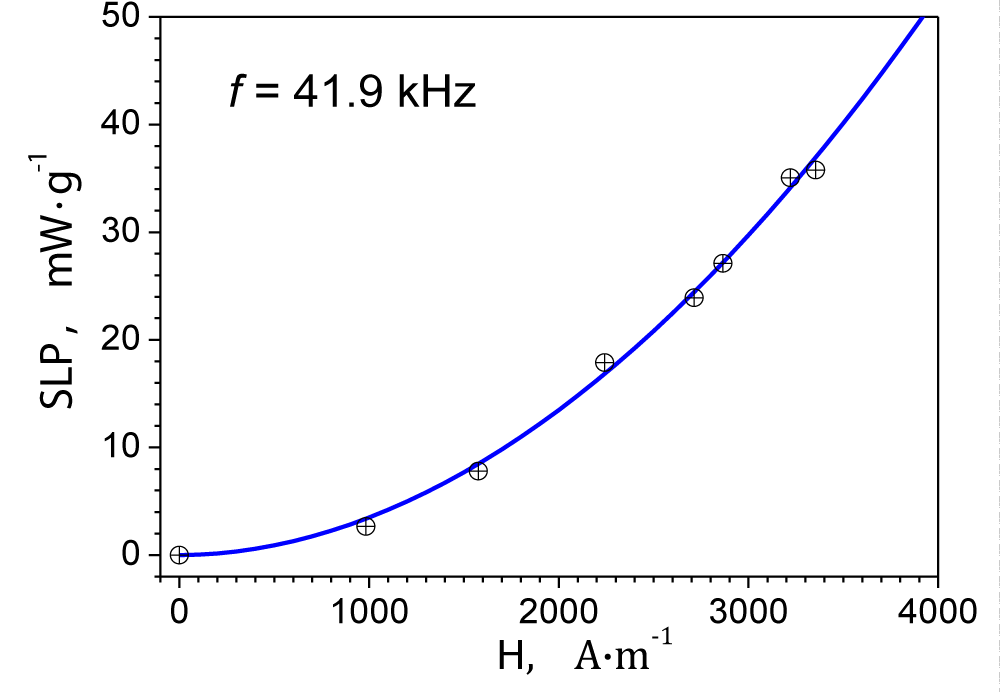
In the experiment with a field strength of H = 4 kA·m-1 and a frequency of f = 41.9 kHz, an SLP value of 52 mW·g-1 can be obtained. The dependence of the SLP parameter on the amplitude of the magnetic field intensity is shown in figure 6.
Figure 6: The specific loss power SLP of MF as a function of magnetic field strength H.
The article presents the construction of the device for generating RMF based on the use of rectangular waveforMS shifted by 90 degrees angles and the use of a selective filter that eliminated higher components and reproduced only the basic, sinusoidal component.
The value of the exponent n = 2 in equation (4) indicates that the main source of the released thermal energy is magnetic relaxation. In addition, the tested MF sample with very small NPs exhibits superparamagnetism. Due to the use of small particles, the dominant mechanism of magnetization followed the Néel’s theory. In future heating studies with RMF, NPs larger sizes should be used and then Brown’s relaxation time will be comparable with Néel’s time. With the diameter (dm) of the magnetite core close to 19 nm and the same other parameters of the sample, both magnetization mechanisms will be equal to each other.
The present research uses spherical-shaped nanoparticles but other types of nanotubes [15] may find a similar application.
- Turkyilmazoglu M. Magnetohydrodynamic moving liquid plug within a micro-channel: Analytical solutions. J Biomech Eng. 2021; 143: 011012.
- Turkyilmazoglu M. Single phase nanofluids in fluid mechanics and their Hydrodynamic linear stability analysis. Comput Methods Programs Biomed. 2020; 187: 105171. PubMed: https://pubmed.ncbi.nlm.nih.gov/31785535/
- Turkyilmazoglu M. Nanoliquid film flow due to a moving substrate and heat transfer. Eur Phy J Plus. 2020; 135: 781.
- Turkyilmazoglu M. Effects of uniform radial electric field on the MHD heat and fluid flow due to a rotating disk. Int J Eng Sci. 2011; 51: 233-240.
- Rosensweig RE. Heating magnetic fluid with alternating magnetic field. J Magn Magn Mater. 2002; 252: 370-374.
- Dutz S, Hergt R. Magnetic particle hyperthermia – a promising tumor therapy? 2014; 25: 452001. PubMed: https://pubmed.ncbi.nlm.nih.gov/25337919/
- Skumiel A, Leszczyński B, Molcan M, Timko M. The comparison of magnetic circuits used in magnetic hyperthermia. J Magn Magn Mater. 2016; 420: 177-184.
- Beković M, Trlep M, Jesenik M, Hamler A. A comparison of the heating effect of Magnetic fluid between the alternating and rotating magnetic field. J Magn MagnMater. 2014; 355: 12-17.
- Sharapova VA, Uimin MA, Mysik AA, Ermakov AE. The Physics of Metals and Metallography, Heat Release in Magnetic Nanoparticles in AC Magnetic Fields. 2010; 110: 5-12.
- Egolf PW, Shamsudhin N, Pane S, Vuarnoz D, Pokki J, et al. Hyperthermia with rotating magnetic nanowires inducing heat into tumor by fluid friction. J Appl Phy. 2016; 120: 064304.
- Eisberg RM, Lerner LS. Physics, Foundations and Applications, McGraw-Hill Book Company, New York, Magnetic Dipoles and Their Applications, 1981; 24: 1140-1149.
- Landau LD, Lifszyc EM. Viscous Liquid, Flow for small Reynolds numbers, Hydrodynamics, Wydawnictwo Naukowe PWN, Warszawa, Chapter II. 1994: 81-92.
- Skumiel A, Hornowski T, Józefczak A, Koralewski M, Leszczyński B. Uses and limitation of different thermometers for measuring heating efficiency of magnetic fluids. Appl Ther Engi. 2016; 100: 1308-1318.
- Skumiel A, Kaczmarek-Klinowska M, Timko M, Molcan M, Rajnak M. Evaluation of powerheatlosses in multidamain iron particlesunder the influence of AC magnetic field in RF Range. Int J Thermophysics. 2013.
- Skumiel A, Kertmen A, Nowaczyk G. Investigation of the magnetic Hyperthermia effect in anaqueous dispersion of colloidosomal nanoparticle clusters. J Mol Liquids. 2019; 283: 91–95.