More Information
Submitted: November 10, 2022 | Approved: January 04, 2023 | Published: January 06, 2023
How to cite this article: Suhir E. Failure-oriented-accelerated-testing (FOAT) and its role in assuring electronics reliability: review. Int J Phys Res Appl. 2023; 6: 001-018.
DOI: 10.29328/journal.ijpra.1001048
Copyright License: © 2023 Suhir E. This is an open access article distributed under the Creative Commons Attribution License, which peRmits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Failure-oriented-accelerated-testing (FOAT) and its role in assuring electronics reliability: review
E Suhir*
Bell Laboratories, Murray Hill, NJ (ret), Portland State University, Portland, OR and ERS Co., Los Altos, CA, 94024, USA
*Address for Correspondence: E Suhir, Bell Laboratories, Murray Hill, NJ (ret), Portland State University, Portland, OR and ERS Co., Los Altos, CA, 94024, USA, Email: [email protected]
A highly focused and highly cost-effective failure-oriented-accelerated-testing (FOAT) suggested about a decade ago as an experimental basis of the novel probabilistic design for reliability (PDfR) concept is intended to be carried out at the design stage of a new electronic packaging technology and when high operational reliability (like the one required, e.g., for aerospace, military, or long-haul communication applications) is a must. On the other hand, burn-in-testing (BIT) that is routinely conducted at the manufacturing stage of almost every IC product is also of a FOAT type: it is aimed at eliminating the infant mortality portion (IMP) of the bathtub curve (BTC) by getting rid of the low reliability “freaks” prior to shipping the “healthy” products, i.e., those that survived BIT, to the customer(s). When FOAT is conducted, a physically meaningful constitutive equation, such as the multi-parametric Boltzmann-Arrhenius-Zhurkov (BAZ) model, should be employed to predict, from the FOAT data, the probability of failure and the corresponding useful lifetime of the product in the field, and, from the BIT data, as has been recently demonstrated, - the adequate level and duration of the applied stressors, as well as the (low, of course) activation energies of the “freaks”. Both types of FOAT are addressed in this review using analytical (“mathematical”) predictive modeling. The general concepts are illustrated by numerical examples. It is concluded that predictive modeling should always be conducted prior to and during the actual testing and that analytical modeling should always complement computer simulations. Future work should be focused on the experimental verification of the obtained findings and recommendations.
The bottleneck of an electronic, photonic, MEMS or MOEMS (optical MEMS) system’s reliability is, as is known, the mechanical (“physical”) performance of its materials and structural elements [1-5] and not its functional (electrical or optical) performance, as long as it is not affected by the mechanical behavior of the design. It is well known also that it is the packaging technology that is the most critical undertaking, when making a viable, properly protected, and effectively-interconnected electrical or optical device and package into a reliable product. Accelerated life testing (ALT) [6-15], conducted at different stages of an IC package design and manufacturing is the major means for achieving that. Burn-in-testing (BIT) [16-23], the chronologically final ALT, aimed at eliminating the infant mortality portion (IMP) of the bathtub curve (BTC) prior to shipping to the customer(s) the “healthy” products, i.e. those that survived BIT, is particularly important: BIT is, therefore, an accepted practice for detecting and eliminating possible early failures in the just fabricated products and is conducted at the manufacturing stage of the product fabrication. Original BITs used continuously powering the manufactured products by applying elevated temperatures to accelerate their aging, but today various stressors, other-than-elevated-temperature, are employed in this capacity. BIT, as far as “freaks” are concerned, is and always has been, of course, a FOAT type of testing.
But there is also another, so far less well-known and not always conducted today, FOAT [24-29], that has been recently suggested in connection with the probabilistic design for reliability (PDfR) concept [30-48]. Such a design stage FOAT, if decided upon, should be conducted as a highly focused and highly cost-effective undertaking. FOAT is the experimental foundation of the PDfR concept and, unlike BIT, which is always a must, should be considered, when developing a new technology or a new design, and when there is an intent to better understand the physics of failure and, for many demanding applications, such as, e.g., aerospace, military, or long-haul communications, to quantify the lifetime and the corresponding, in effect, never-zero, probability of failure of the product. Such a design-stage FOAT could be viewed as a quantified and reliability-physics-oriented forty years old highly-accelerated-life-testing (HALT) [49-52] and should be particularly recommended for new technologies and new designs, whose reliability is yet unclear and when neither a suitable HALT nor more or less established “best practices” exist.
When FOAT at the design stage and BIT at the manufacturing stage is conducted, a suitable and physically meaningful constitutive equation, such as, e.g., the multi-parametric Boltzmann-Arrhenius-Zhurkov (BAZ) model [53-67], should be employed to predict, from the test data, the probability of failure and the corresponding useful lifetime of the product in the field.
Both types of FOAT and the use of the BAZ equation are addressed in this review, and their roles and interaction with other types of accelerated tests are indicated and discussed. Our analyses use, as a rule, analytical (“mathematical”) predictive modeling [68-74]. In the author’s opinion and experience, such modeling should always complement computer simulations: these two major modeling tools are based on different assumptions and use different computation techniques, and if the calculated data obtained using these tools are in agreement, then there is a good reason to believe that the obtained data are accurate and trustworthy.
Failure-oriented-accelerated-testing (FOAT)
Accelerated testing: Accelerated testing [6-8] (Table 1) is a powerful means to understand, prove, improve and assure an electronic or a photonic product’s reliability at all stages of its life, from conception to failure (“death”).
| Table 1: Accelerated test types. | |||||
| Test type | Product development testing (PDT) |
Highly accelerated life testing (HALT) |
Qualification testing (QT) | Burn-in testing (BIT) |
Failure oriented accelerated testing (FOAT) |
| Objective | Assurance that the considered design approach and materials selection are acceptable | Ruggedizing the product and tentatively assessing its reliability limits |
Proof that the product is qualified to serve the given product in the given capacity | Eliminating the infant mortality portion of the bathtub curve (the "freaks") |
Understand the physics of failure, confirm the use of the particular predictive model, and assess the probability of failure |
| Endpoint | Type, time, level, and/or the number of failures | Predetermined number or percent of failures | Predetermined time and/or number of cycles to failure | Predetermined time and/or the loading level | Predetermined number or percent of failures (usually 50%) |
| Follow-up activity | Failure analysis, design decision |
Failure analysis | Pass/fail decision | Shipping the sound products | Failure and probabilistic analyses of the test data |
| Ideal test | Specific definitions | No failures in a long time | Numerous failures in a short time |
||
The product development tests (PDTs) are supposed to pinpoint the weaknesses and limitations of the future design, materials, and/or manufacturing technology or process. These tests are used also to evaluate new designs, new processes, and the appropriate corrective actions, if necessary, and to compare different designs from the standpoint of their expected reliability. This type of testing is followed by the analyses of the observed failures, or by other “independent” investigations, often based on predictive modeling. Typical PDTs are destructive, i.e., are also of the FOAT type. Temperature cycling (see, e.g., [75-80]), twist-off [81], shear-off (see, e.g., [82-84]) and dynamic (see, e.g., [85-87]) tests are examples of PDTs aimed at the selection and evaluation of the bonding material or a structural design. Predictive modeling [88-97] is always conducted at this, initial, stage to design an adequate test, to understand the physics of failures and to make sure that the considered design approach and materials selection is acceptable.
The objective of the qualification tests (QTs) in today’s practices is to prove that the reliability of the product-under-test is above a specified level. In today’s practices, this level is usually determined by the percentage of failures per lot and/or by the number of failures per unit of time (failure rate). Testing is time limited. The analyst usually hopes to get as few failures as possible, and his/hers pass/fail decision is based on a particular accepted go/no-go criterion. Although the QTs are unable (and are not supposed) to evaluate the failure rate, their results can be, nonetheless, sometimes used to suggest that the actual failure rate is at least not higher than a certain value. This can be done, in a very tentative way, on the basis of the observed percent defective in the lot. QTs, in the best-case scenario, are nondestructive, but some level of failure is acceptable. If, however, the PDfR concept is considered, the non-destructive QTs could be conducted as a sort of quasi-FOAT that adequately replicates the initial non-destructive stage of the previously carried out full-scale FOAT whose data, including time-to-failure (TTF) and the mean-time-to-failure (MTTF), are known and available by the time of the QTs.
Understanding the underlying physics of failure is critical, and this is the primary objective of the design stage FOAT. As has been indicated, FOAT conducted at the design stage of the product development is the experimental basis of the PDfR concept. While QT is “testing to pass”, FOAT is “testing to fail” and is aimed at confirming the underlying physics of failure anticipated by the use of a particular predictive model (such as, e.g., multi-parametric BAZ equation), establishing its numerical characteristics (sensitivity factors, activation energies, etc.), predict the probability of failure and the corresponding time-to-failure (TTF) and the mean-time-to-failure (MTTF) and to assess on this basis, using BAZ, the useful lifetime of the product and the corresponding probability of failure in actual operating conditions. There are several more or less well known constitutive FOAT models, other than BAZ, today: power law (used when the physics of failure is unclear, e.g., in proof-testing of optical fibers); Arrhenius’ equation (used when there is a belief that elevated temperature is the major cause of failure, which might be indeed the case when assessing the long-term reliability of an electronic or a photonic material); Eyring’s equation, in which the mechanical stress is considered directly (in front of the exponent); Peck’s equation (the stressor is the relative humidity); inverse power law (such as, e.g., Coffin-Manson’s and related equations used in electronics packaging, when there is a need to evaluate the low cycle fatigue life-time of solder joint interconnections, if the inelastic deformations in the solder material are unavoidable); Griffith’s theory based equations (used to assess the fracture toughness of brittle materials and crack growth; it is noteworthy that Griffith’s fracture mechanics cannot predict the initiation of cracks, but is concerned with the likelihood and the speed of propagation of fatigue and brittle cracks, including delaminations – interfacial cracks); Miner’s rule (used to evaluate the fatigue lifetime when the yield stress is not exceeded and the inelastic strains are avoided); creep rate equations (used when creep is important, often in combination with Coffin-Manson empirical relationships); weakest link model (used to evaluate the TTF in brittle materials with defects); stress-strength interference model, that is widely employed in many areas of reliability engineering to consider, on the probabilistic basis, the interaction of the strength (capacity) of the material and structure of importance and the applied stress (loading); extreme-value-distribution (EVD) based model (used, when there is a reason to believe that it is only the extreme values of the applied stressors contribute to the finite lifetime of the material and device).
A highly focused and highly cost-effective FOAT at the design stage should be conducted for the most vulnerable materials and structural elements of the design (reliability “bottle-necks”) in addition to and, in many cases, even instead of the HALT, especially, as has been indicated, for new products, for which no experience is yet accumulated and no best practices are developed. FOAT is a “transparent box” and could be viewed as an extension and a modification of the forty years old HALT, which is a “black box”. HALT is currently widely employed in different modifications, with an intent to determine the product’s reliability weaknesses; assess, in a qualitative way, the reliability limits; ruggedize the product by applying elevated stresses (not necessarily mechanical and not necessarily limited to the anticipated field stresses) that could cause field failures; and to provide, hopefully, large, but, actually, unknown, safety margins over expected in-use conditions. HALT tries to “kill many unknown birds with one big stone” and is considered to be a “discovery” test. HALT can precipitate and identify failures of different types and origins and even tentatively assess the reliability limits. HALT does that through a “test-fail-fix” process, in which the applied stresses (“stimuli”) are somewhat above the specified operating limits, but HALT does not consider the physics of failure and is unable to quantify probability on any basis, whether deterministic or probabilistic. HALT can be used, however, for “rough tuning” of product’s reliability, while FOAT could be employed, when “fine-tuning” is necessary, i.e., when there is a need to quantify, assure and even, if possible and appropriate, specify the operational reliability of the device or package. FOAT could be viewed therefore as a quantified and reliability physics-oriented HALT. If one sets out to understand the physics of failure to create a highly reliable product, conducting FOAT at its design stage is imperative. Both HALT and the design stage FOAT should be geared, of course, to a particular technology, product, and application.
Probabilistic design for reliability (PDfR) concept
Reliability engineering is viewed in this concept as part of applied probability and probabilistic risk management bodies of knowledge and includes the product’s dependability, durability, maintainability, reparability, availability, testability, etc., as probabilities of occurrence of the reliability-related events and characteristics of interest. Each of these characteristics could be, of course, of greater or lesser importance, depending on the particular product, its intended function, operation conditions, and consequences of its possible failure. The PDfR concept proceeds from the recognition that nothing is perfect, and that the difference between a highly reliable and an insufficiently robust product is “merely” in the level of their never-zero probability of failure. This probability cannot be high, of course, but does not have to be lower than necessary either: it has to be adequate for a particular product and application. An over-engineered and superfluously robust product that “never fails” is, more likely than not, more costly than it could and should be (see section 10 of this write-up).
Application of the probabilistic risk analysis concepts, approaches, and techniques puts the reliability assurance on the consistent and “reliable” ground and converts the art of creating reliable packages into a physics-of-failure- and applied-probability-based science. If such an approach is adopted, there will be a reason to believe that an IC package that underwent HALT, passed the established (desirably, improved) QT, and survived BIT will not fail in the field, owing to the predicted and very low probability of possible failure (see section 3 of this review). By conducting FOAT for the most vulnerable materials and structural elements of the design and by providing a physically meaningful, quantifiable and sustainable way to create a “generically healthy” product, the PDfR concept enables converting the art of designing reliable packages into physics-of-failure and applied-probability based science. After the probability of the operational failure predicted from the FOAT data is evaluated, sensitivity analysis could be carried out, if necessary, to determine what could possibly be changed to establish the adequate level of this probability, if there is a need for that. Such an analysis does not require any significant additional effort, because it would be based on the already developed methodologies and algorithms.
It is noteworthy that reliability evaluations should be conducted for the product of importance on a permanent basis: the reliability is “conceived” at the early stages of its design, implemented during manufacturing, qualified, and evaluated by electrical, optical, environmental, and mechanical testing, checked (screened) during production, and, if necessary and appropriate, maintained in the field during the product’s operation. The prognostics and health monitoring (PHM) methods and approaches would have much better chances to be successful if a “genetically healthy” package is created. Thus, the PDfR concept enables to improve dramatically the state-of-the-art in the IC packaging reliability. The main features of the PDfR concept could be summarized by the following ten requirements (“commandments”): 1) The best product is the best compromise between the needs (requirements) for its reliability, cost-effectiveness and time-to-market (completion); 2) Reliability of an IC product cannot be low, but need not be higher than necessary: it has to be adequate for a particular product and application; 3) When adequate, predictable and assured reliability is crucial, ability to quantify it is imperative, especially if high reliability is required and if one intends to optimize reliability; 4) One cannot design a product with quantified and assured reliability by just conducting HALT; this type of accelerated testing might be able to identify weak links in the product, but does not quantify reliability; 5) Reliability evaluations and assurances cannot be delayed until the product is made and shipped to the customer, i.e., cannot be left to the highly popular today PHM effort, important as this activity might be; the PDfR effort is aimed, first of all, at designing a “genetically healthy” product, thereby making the PHM effort, if needed, more effective; 6) Design, fabrication, qualification, PHM and other reliability related efforts should consider and be geared to the particular device and its intended application(s); 7) PDfR concept is an effective means for improving the state-of-the-art in the field of IC packaging; 8) FOAT is an important feature of PDfR; FOAT is aimed at understanding the physics of failure, and at validation of a particular physically meaningful predictive model; as has been indicated, FOAT should be conducted in addition to, and sometimes even instead of HALT; 9) Predictive modeling is another important constituent of the PDfR and, in combination with FOAT, is a powerful, cost-effective and physically meaningful means to predict and eliminate failures; 10) Application of consistent, comprehensive and physically meaningful PDfR can lead to the most feasible QT methodologies, practices, procedures and specifications.
Possible classes of IC products from the standpoint of their reliability level
Three classes of electronic or photonic products could be distinguished and considered from the standpoint of the requirements for their reliability, including the acceptable probability of failure: 1) The product has to be made as reliable as possible; failure is a catastrophe and should not be permitted; cost although matters, but is of a minor importance; examples are military, space or other products, which, in general, are not manufactured in large quantities; examples are electronics in a nuclear bomb, or in a spacecraft, or in a long-haul communication system; 2) The product is mass produced, has to be made as reliable as possible, but only for a certain level of demand (stress, loading); failure is still a catastrophe, but, unlike in the previous class, cost plays an important role; 3) Reliability does not have to be high at all; failures are permitted, but still should be understood and, to an extent possible, restricted; examples are consumer, commercial, and agricultural electronic devices. These classes differ by the acceptable (specified) probability of failure and the corresponding lifetime.
It should be mentioned in this connection that the assessed and established, based on the rules of classification societies, probability that the hull of an ocean-going vessel sailing for twenty years in a row in the North Atlantic, which is the most severe, from the standpoint of wave and wind condition, region of the world ocean, breaks in half is 10-7 - 10-8 (see, e.g., [98,99]). With this in mind, one could require, e.g., that the probability of failure of an electronic or a photonic product of the above three classes is, say 10-6, 10-5 and 10-4, respectively. This is because of many favorable factors that affect the probability of failure of a product, and completely different consequences of failure.
Multi-Parametric Boltzmann-Arrhenius-Zhurkov(BAZ)Equation:
The equation
(1)
Was suggested by (a Russian physicist) Zhurkov [58,59] in the experimental fracture mechanics as a generalization of the (Swedish physical chemist) Arrhenius’ equation [56,57].
(2)
In the kinetic theory of chemical reactions to evaluate the meantime τ to the commencement of the reaction. In Zhurkov’s theory τ is the mean time to failure (MTTF). Equation (2) states that a certain level of the ratio of the “activation energy” U0 to the thermal energy kT, which k = 8.6173x0-5= eV/K is Boltzmann’s constant and T is the absolute temperature, is required for the chemical reaction to get started. When used in fracture mechanics, an effective activation energy triggers crack propagation, i.e., characterizes the propensity of the material to the anticipated failure mechanism. This mechanism is characterized in fracture mechanics by a certain level of the strain energy release rate. In equations (1) and (2), τ0 is an experimentally obtained time constant. The term “activation energy” was coined by Arrhenius. Equation (2) is formally not different from the (Austrian physicist) Boltzmann’s equation in the thermodynamic theory of ideal gases [53-55]. The equation (1) was used by Zhurkov and his associates when conducting numerous mechanical tests, in which the external tensile stresses σ were applied to notched specimens at different elevated temperatures T, i.e. when the mechanical stress and the elevated temperature contributed jointly to the finite mechanical/physical lifetime of the materials under test.
The τ value is, in effect, the maximum value of the probability of non-failure. Indeed, using the exponential law of reliability P = exp(-λt) and considering that the failure rate λ is reciprocal to the MTTF this law can be written as
(3)
Introducing (1) into this equation, the following double-exponential-distribution for the probability of non-failure can be obtained:
. (4)
The time derivative of this distribution is where H(P) = PIn P is the entropy of the distribution. This derivative explains the physical rationale behind the distribution (4): the probability of non-failure decreases with an increase in the time of operation or testing and increases with an increase in the entropy of the distribution. The entropy H(P) is zero at the initial moment of time (t = 0), when the probability of non-failure is P = 1, and at the remote moment of time (t → ∞), when P = 0. Its maximum value found from the condition is . The probability P = P* that corresponds to the maximum entropy Hmax determined from the equation is also . Then the formula (3) indicates that the maximum probability of non-failure takes place at the moment of time t = , which is the MTTF of the physical process in question.
It has been recently suggested [56-87] that any stimulus (stressor) of importance (voltage, current, thermal stress, elevated humidity, vibrations, radiation, light output, etc.) or an appropriate combination of these stimuli can be used to stress a microelectronic or a photonic material, device, package or a system subjected to FOAT. It was suggested also that the time constant in the equations (1) or (2), can be replaced, when FOAT is considered and depending on the application and the specifics of the particular FOAT, by a suitable quantity that characterizes the degradation process, such as, e.g., the product γII*, when the leakage current I is viewed as an acceptable and measurable quantity during FOAT (here I* is its critical value, and γI is the sensitivity factor), or the product γRR*, when the measured electrical resistance R is selected as an acceptable degradation criterion and its critical value R* is an indication of the occurred failure (here γR is the sensitivity factor for the electrical resistance). Then, in the general case, such a multi-parametric BAZ equation can be written as
(5)
Here C* is the critical value (an indication of the occurred failure) of the selected, agreed upon, measurable, and monitored criterion C of the level of damage (such as, say, leakage current or electrical resistance, or energy release rate), γC is its sensitivity factor, t is time, σi is the i-th stressor, γi is its sensitivity factor and kT is the thermal energy.
Baz example: humidity-voltage bias
If, e.g., the elevated humidity H and the elevated voltage V are selected as suitable FOAT stressors, and the leakage current I - as the suitable measurable and monitored during the FOAT characteristic of the accumulated damage, then equation (5) can be written as
(6)
The sensitivity factors and the activation energy can be determined by conducting a three-step FOAT. In the first step testing should be carried out for two different temperatures, T1 and T2, keeping the levels of the relative humidity H and the elevated voltage V the same in both tests. Recording the percentages P1 P2 of non-failed samples for the testing times t1 and t2, when failures occur, i.e., when the monitored leakage current I reaches its critical value I*, the following relationships could be obtained:
(7)
Since the numerator U = U0 - γHH -γVV in these relationships is kept the same, the following condition should be fulfilled for the sensitivity factor γI:
. (8)
This condition could be viewed as an equation for the γI value and has the following solution:
(9)
In the second step, FOAT at two relative humidity levels H1 H2 should be conducted for the same temperature and voltage. This yields:
(10)
Similarly, by changing the voltages V1 and V2 at the third step of FOAT one obtains:
(11)
Finally, the stress-free (“effective”) activation energy can be found in (6) as
(12)
for any consistent combination of humidity, voltage, temperature, and time.
Let, e.g., after t1 = 35h testing at the temperature of T1 = 80 0C = 353K, the voltage of V = 600 V and the relative humidity of H = 0.85%, the allowable (critical) level I* = 3.5µA of the leakage current was exceeded in 10% of the tested samples so that the probability of non-failure is P1 = 0.9. After t2 = 70h testing at the somewhat higher temperature of T2 = 120 0C =393K, but at the same voltage and the same humidity, 60% of the tested devices exceeded the above critical level so that the probability of non-failure was only P2 = 0.4 Then the second formula in (8) yields:
and the sensitivity factor for the leakage current in the situation in question can be found in (9) as
Then we obtain:
. This concludes the first FOAT step. In the second step, tests at two relative humidity levels H1 H2 were conducted for the same tempera-ture and voltage. Let, e.g., after t1 = 40h testing at the relative humidity level of H1 = 0.5 at the voltage V = 600 V and temperature T = 60 0C = 333K. 5% of the test specimens failed (P1 = 0.95) and after t2 = 55hat the same temperature and the relative humidity level of H2 = 0.85, 10% the test specimens failed (P2 = 0.90). Then
The sensitivity factor for the relative humidity can be found in (10) as
In the third step, FOAT at two different voltage levels, V1 = 600 V and V2 = 1000V, have been carried out, for the same temperature-humidity bias, T = 85 0C =358K and H = 0.85, it has been determined that 10% the tested specimens failed after t1 = 40h testing (P1 = 0.9) and 20% of the specimens failed after t2\ = 80h of testing (P2 = 0.8). Then we obtain:
and
the calculated sensitivity factor for the voltage stressor is
The calculated activation energy is therefore
No wonder the stress-free activation energy is determined primarily by the third term in this equation. In an approximate analysis, only this term that characterizes the materials could be considered. On the other hand, the level of the applied stressors is also important: in this example, the stressors contributed about 6.4% to the total activation energy. As is known, the activation energy is equal to the difference between the threshold energy needed for the reaction and the average kinetic energy of all the reacting molecules/particles, but, as evident from the carried out example, this difference could be affected by the type and level of the external loading as well. It is noteworthy also that although the input data in this example are hypothetical (but, hopefully, more or less realistic), the level of the obtained activation energy is not very far away from what is reported in the literature. Activation energies for some typical failure mechanisms in semiconductor devices are: for semiconductor device failure mechanisms the activation energy ranges from 0.3eV to 0.6eV; for inter-metallic diffusion, it is between 0.9 and 1.1eV. For metal migration 1.8eV; for charge injection 1.3eV; for ionic contamination 1.1eV; for Au-Al inter-metallic growth 1.0eV; for surface charge accumulation 1.0eV; for humidity-induced corrosion 0.8eV -1.0eV; for electro-migration of Si in Al 0.9eV; for Si junction defects 0.8eV; for charge loss 0.6eV; for electro-migration in Al 0.5eV; for metallization defects 0.5eV. Some manufacturers use the Arrhenius law with an activation energy of 0.7eV for whatever material and the actual failure mechanism might be.
Baz example: Hall’s concept
Pete M. Hall [75] suggested in his, now classical, experimental approach to the assessment of the reliability of solder joint interconnections experiencing inelastic deformations that the interconnection under test be placed between a ceramic chip carrier (CCC)/package and a printed circuit board (PCB). During temperature excursions, the solder joints experience thermal strains caused by the CTE mismatch of the chip carrier and the board. The possible failure modes were electrical failures (“opens”). Hall measured, using strain gages, the in-plane and bending deformations of the CCC and the PCB and, based on these measurements, calculated the forces and moments experienced by the solder joints. The most important finding in Hall’s investigation is that “upon repeated temperature cycling, there is a repeatable stress-strain hysteresis, which is attributed to plastic deformations in the solder”. In Hall’s experiments, the gages were placed on both sides of the CCC (package). The strains in his experiments were measured in the middle of the assembly and it was assumed that they were “isotropic and uniform” in the plane. An important simplification in Hall’s experiments was the consideration of a “model with axial symmetry”, assuming “that the solder posts can be treated as if they were in a circular array and thus all equivalent”. This is, of course, not the case in actually soldered assemblies: it is the peripheral joints that exhibit the highest deformations. The strength and the novelty of pioneering P. Hall’s work are in the experimental part of his effort. The strains were measured as functions of temperature using commercial metal foil strain gages. Hall concludes that plots of the thermally induced force vs. displacement “can be used to yield the plastic strain energy dissipated per cycle in the solder” and that “this energy can be used to quantify micro-structural damage and eventually to predict lifetimes in thermal chamber cycling”. It is this recommendation that is used in the analysis that follows. We apply, however, more realistic assumptions for the phenomena of interest, when using the BAZ model.
The probability of non-failure of a solder joint inter-connection experiencing inelastic strains during temperature cycling can be sought in the form of the BAZ equation as follows:
. (13)
Here U0, eV, is the activation energy which is the characteristic of the solder material’s propensity to fracture, W, eV, is the damage caused by a single temperature cycle and measured, in accordance with Hall’s concept, by the hysteresis loop area of a single temperature cycle for the strain of interest, T is the absolute temperature (say, the cycle’s mean temperature), n is the number of cycles, k, eV/K is Boltzmann’s constant, t, S, is time, R, Ω is the measured (monitored) electrical resistance at the joint location, and is the sensitivity factor for the electrical resistance R. The equation (13) makes physical sense. Indeed, the probability P of non-failure is zero at the initial moment of time t = 0 and/or when the electrical resistance R of the joint material is zero. This probability decreases, because of material aging and structural degradation, with time, and not necessarily only because of temperature cycling. It is lower for higher electrical resistance (resistance of, say, 450Ω can be viewed as an indication of an irreversible mechanical failure of the joint). Materials with higher activation energy U0 have a lower probability of possible failure. The increase in the number of cycles n leads to a lower effective activation energy U = U0- nW and so does the level of the energy W of a single cycle. The MTTF τ is
(14)
Mechanical failure, associated with temperature cycling, occurs, when the number n of cycles is When this condition takes place, the temperature in the denominator in the parentheses of the equation (13) becomes irrelevant, and this equation results in the following formula for the probability of non-failure:
(15)
The MTTF is
(16)
If, e.g., 20 devices have been temperature cycled and the high electrical resistance Rf = 450Ω, considered as an indication of failure was detected in 15 of them, then Pf = 0.25. If the number of cycles during such a FOAT were, say, nf = 2000 and each cycle lasted, say, 20 min = 1200s, then the predicted TTF is tf = 2000x1200 = 24x105 s = 27.7778 days, and the formulas (15) and (16) yield:
Note that the MTTF is naturally and appreciably shorter than the TTF. Let, e.g., the area of the hysteresis loop was W = 4.5x10-4 eV. Then the stress-free activation energy of the solder material is U0 = nfW = 2000x4.5x10-4 = 0.9eV. To assess the number of cycles to failure in actual operation conditions one could assume that the temperature range in these conditions is, say, half the accelerated test range and that the area W of the hysteresis loop is proportional to the temperature range. Then the number of cycles to failure is . If the duration of one cycle in actual operation conditions is, say, one day, then the time to failure will be tf = 7200 days = 19.726 years.
Baz example: Optical silica fiber intended for outer space applications
Considering a situation, when an optical silica fiber, intended for space applications, is subjected to the combined action of low temperatures T, tensile stress σ, ionizing radiation D and random vibrations of the magnitude V, of its time-dependent probability P = P(t) of non-failure could be sought in the form:
(17)
Here t is time, T temperature, kT thermal energy,
U = U0 + γσ σ + γDD + γV S
(18)is the effective activation energy, U0 is the stress-free activation energy and the γ factors reflect the fiber sensitivities, as far as its propensity to fracture is concerned, to the changes in the applied stressors: γt - to the change in temperature, γσ - to the change in the tensile stress, γD - to the change in the ionized radiation and γV - to the change in the level of random vibrations. Note that as long as the activation energies U and U0 the thermal energy kT are expressed in eV, the factor γσ is expressed in eVkg-1 mm2, if the applied tensile stress is in kg/mm2; the factor γD - in eVGγ-1, if the absorbed dose of ionizing radiation is measured in Grays (as is known,1.0Gy or 1.0Gray is the SI unit of absorbed dose of ionizing radiation equal to 1 joule of radiation energy absorbed per one kg of matter), and the factor γV is in eVxHzx(m/s2)-2 if the level of the random vibrations is measured in (vibration acceleration squared per unit frequency). It is noteworthy that if other more or less significant loadings act concurrently with those considered in the formula (18), these loadings could be also considered in this formula for the effective activation energy.
The distribution (17) contains five empirical parameters: the stress-free activation energy U0 and four sensitivity factors γ the time factor γt, the tensile stress factor γσ, the radiation factor γD, and the random vibrations factor γV. These factors and the activation energy U0 could be obtained from a four-step FOAT. In the first step it should be conducted for two temperatures, T1 and T2, keeping all the stressors that determine the effective activation energy U the same, whatever their level is. After recording the percentages P1 P2 of the on-failed samples the following relationships can be obtained:
(19)
Here t1 t2 are the times, at which failures occurred. Since the effective activation energies U values were kept the same in these relationships, the condition
(20)
Must be fulfilled. Viewing this condition as an equation for the time sensitivity factor γt, we obtain:
(21)
Where the notations
(22) are used. It is advisable, of course, that more than two FOAT series and more than two temperature levels are considered so that the sensitivity parameter γt is evaluated with a high enough degree of accuracy. In the second step testing at two stress-temperature levels σ1 and T1, and σ2 T2, should be conducted, while keeping, within this step of FOAT, the levels of the radiation D and the random vibration S the same in both sets of tests. Then the following equations could be obtained for the probabilities of non-failure:
(23)
The unchanged amount in these tests is where the notations (22) are used. Hence, the sensitivity factor γσ can be obtained from the equation that yields:
(24)
The time-probability parameters n1 n2 are, of course, different at each step and should be based on the probabilities of non-failure and the corresponding times at the given step. Similarly, by keeping at the third step of FOAT the levels of stresses σ and random vibration spectrum in both sets of tests the same, and conducting the tests for two radiation-temperature levels, the following formula for the radiation sensitivity factor γD can be obtained:
(25)
In the fourth step testing at two vibration-temperature levels should be conducted, while keeping the levels of tensile stress and radiation the same. Then, using the same considerations as above, the following formula for the sensitivity factor γV can be obtained:
(26)
The effective activation energy U can be evaluated now from (19) as
(27)
and the stress-free activation energy can be found in (18):
U0 = U + γσσ + γDD + γVS (28)
The expected static fatigue lifetime (time-to-failure, remaining useful life) can be determined from (17) for the given probability P of non-failure as
(29)
This time is, of course, the probability of non-failure P dependent and changes from infinity to zero, when this probability changes from zero to one.
Let, e.g., the following input FOAT information was obtained at the first step of testing: 1) After t1 = 10h testing at the temperature of T1 = 200 OC = 73K under the tensile stress of σ = 420kg/mm2, 25% of the test specimens failed, so that the probability of non-failure is P1 = 0.75 in these tests; 2) After t2 = 8.0h of testing at the temperature of T2 = 250 OC = 23K under the same tensile stress, 10% of the samples failed so that the probability of non-failure is P2 = 0.90. Then the second formula in (20) and the formula (22) yield:
and the formula (21) results in the following value of the time sensitivity factor:
As one could see from the further evaluations, this sensitivity factor is particularly critical because it affects the other sensitivity factors. In the second step testing is conducted at the stress levels of σ1 = 400kg/mm2 and σ2 = 400kg/mm2 at the temperatures T1 = 200 OC = 73K and T2 = 150 OC = 23K respectively, and it has been confirmed that, indeed, 25% of the samples tested under the stress σ1 = 420kg/mm2 failed after t1 =10.0h testing, so that indeed P1 = 0.75. The percentage of samples failed at the stress level of σ2 = 400kg/mm2 was 10% after t2 =5.0h of testing, so that P2 = 0.90. Then, as follows from (11),
In the third step radiation tests have been conducted, and it has been established that 1) After t1 = 35h testing at the temperature of T1 = 270 OC = 3K and after the total ionizing dose of D2 = 1.0Gy = 1.0J/kg (one joule of radiation energy absorbed per kilogram of matter) was obtained, 65% of the tested specimens failed, so that the recorded probability of non-failure was P1 = 0.35; and that 2) After t2 =50h of testing at the temperature of T2 = 250 OC = 23K and at the radiation level of D2 = 2.0Gy = 2.0J/kg, 80% of the tested samples failed, so that the recorded probability of non-failure was P2 = 0.20. Then the formula (25) yields:
In the fourth step, FOAT for random vibrations was conducted. Testing was carried out in two sets. The tensile stress (force) and the level of radiation were kept the same in both of them. The first set of tests was run t1 = 12h at the temperature of T1 = 180 OC = 93K under the vibration level of S1 = 2.0mm2s-3 and it was observed that 80% of the specimens failed by that time P1 = 0.2. The second set of tests was run t2 = 7h at the temperature of T2 = 250 OC = 23K under the lower vibration level of S2 = 1.0mm2s-3 and it was observed that only 40% of the tested specimens failed by that time, so that P2 = 0.6. Then the predicted sensitivity factor γV for the random vibrations is
The effective activation energy U can be determined from (14) for either of the two FOAT steps as
and is, of course, very low. The stress-free activation energy can be then found in (15) as
The TTF t (in hours) can be evaluated for different temperatures and for different probabilities of non-failure using the formula (28):
The calculated data are shown in Table 2. As evident from these data, the TTF at ultra-low temperatures (note that the BAZ equation assumes that the life-time at zero absolute temperature might be next-to-infinity) and at high values of the required (or expected) probabilities of non-failure are very sensitive to the changes in the operation temperatures and in the corresponding probabilities of non-failure.
| Table 2: Time-to-failure (TTF) in hours depending on the probability-of-non-failure and temperature. | |||||||
| T, K T0 C |
20 -253 |
40 -233 |
60 -213 |
80 -193 |
100 -173 |
150 -123 |
250 -23 |
| P | Time-to-failure (TTF) in hours | ||||||
| 0.80 | 20.095 | 10.4311 | 8.3833 | 7.5155 | 7.0385 | 6.4493 | 6.0137 |
| 0.90 | 9.4880 | 4.9252 | 3.9583 | 3.5486 | 3.3234 | 3.0452 | 2.8395 |
| 0.95 | 4.6191 | 2.3978 | 1.9271 | 1.7276 | 1.6179 | 1.4825 | 1.3824 |
| 0.99 | 0.9051 | 0.4699 | 0.3776 | 0.3385 | 0.3170 | 0.2905 | 0.2709 |
PDfR example: Adequate heat sink
As a simple PDfR example, examine a package whose probability of non-failure during steady-state operation is determined by the Arrhenius equation.
(30)
This equation can be obtained from (4) by putting the external stress σ equal to zero. Solving this equation for the temperature, we have:
Let for the given type of failure (say, surface charge accumulation), the ratio of the activation energy to the Boltzmann’s constant is and the time constant τ0 predicted on the basis of the FOAT is τ0 = 5x10-8 h. Let the customer of the particular package manufacturer requires that the probability of failure at the end of the device service time of, say, t = 40,000h ≈ 4.6 years does not exceed Q = 10-5 (see section 3), i.e., acceptable, if not more than one out of hundred thousand devices fails by that time. The above formula indicates that the temperature of the steady-state operations of the heat-sink in the package should not exceed T = 349.8K = 76.8 0C. Thus, the heat sink should be designed accordingly, and the corresponding reliability requirement should be specified for the vendor that provides heat sinks for this manufacturer.
PDfR example: Seal glass reliability in a ceramic package design
The case of identical ceramic adherence was considered in connection with choosing the adequate coefficient of thermal expansion (CTE) for solder (seal) glass in a ceramic package design [99]. The package was manufactured at an elevated temperature of about 900 0C and hundreds of fabricated packages fell apart when they were cooled down to room temperature. It has been established that it happened because the seal glass had a higher CTE than the ceramic body of the package and because of that experienced elevated tensile stresses at low-temperature conditions. Of course, the first step to improve the situation was to replace the existing seal glass with glass whose CTE is lower than that of the ceramics. Two problems, however, arise: first, the compressive stress experienced by the solder glass at low temperatures is applied to this material through its interfaces with the ceramics and should not be too high, otherwise structural failure might occur because of the high interfacial shearing and peeling stresses, and second, both the ceramics and the seal glass are brittle materials, and their properties and, first of all, their CTEs are, in effect, random variables, and therefore the problem of the interfacial strength of the solder glass has to be formulated as the problem that the seal glass at low-temperature conditions is in compression, but this compression, although guaranteed, should be rather moderate, i.e., the probability that the acceptable interfacial thermal stress level is exceeded should be sufficiently low. Accordingly, the problem of the adequate strength of the seal glass interface was formulated as the PDfR problem, and no single failure was observed in the packages fabricated in accordance with the design recommendations obtained on this basis.
Is it possible that your product is superflously and unnecessarily robust?
While many packaging engineers feel that electronic industries need new approaches to qualify and assure the devices’ operational reliability, there exists also a perception that some electronic products “never fail”. The very existence of such a perception might be attributed to the superfluous and unnecessary robustness of the particular product for the given application. Could it be proven that a particular IC package is indeed “over-engineered”? And if this is the case, could the superfluous reliability be converted into appreciable cost-reduction of the product? To answer these questions one has to find a consistent and trustworthy way to quantify the product‘s robustness. Then it would become possible not only to assure its adequate performance in the field but also to determine if a substantiated and well-understood reduction in its reliability level could be translated into appreciable cost savings.
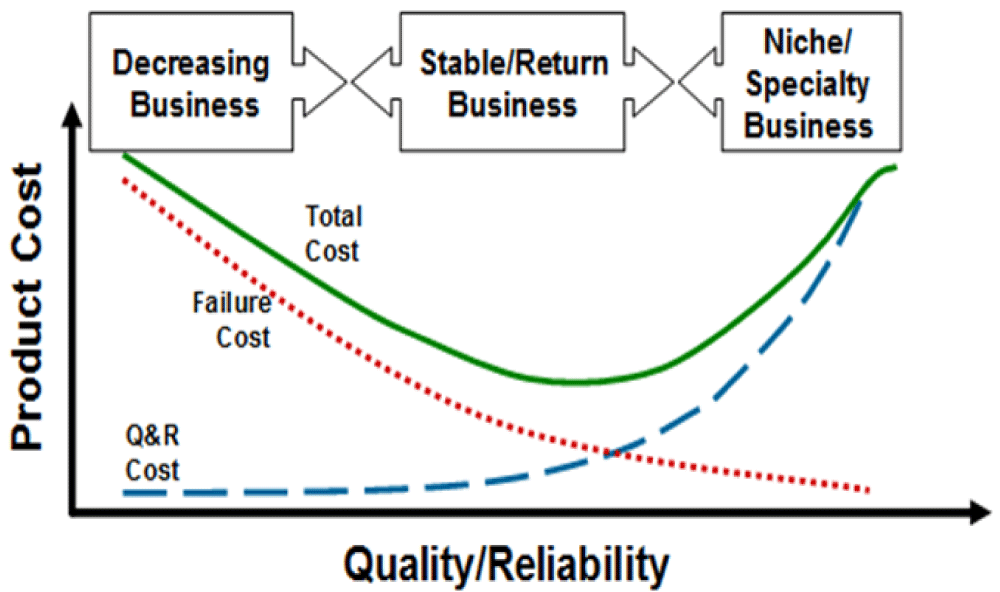
The best product is, as is known, the best compromise between reliability, cost-effectiveness, and time-to-market. The PDfR concept makes it possible to optimize reliability, i.e., to establish the best compromise between reliability, cost-effectiveness, and time-to-market (completion) for a particular product and application. The concept enables the developing of adequate QT methodologies, procedures, and specifications, with consideration of the attributes of the actual operation conditions, time in operation, consequences of failure, and, when needed and possible, even to specify acceptable risks (the never-zero probability of failure). It is natural to assume that higher reliability costs more money. In the simplest, but nonetheless still physically meaningful, case (Figure 1) [94], it is assumed that the reliability-level-dependent quality-and-reliability (Q&R) cost CR to improve reliability R (whatever its meaningful criterion is) increases exponentially with an increase in the difference between the reliability level R and its referenced (specified) level R0: . Here is the cost to improve reliability at its R0 level and r is the sensitivity factor of the reliability improvement cost.
Similarly, the cost of repair could be sought as a decreasing exponent where CF(0) is the cost of removing failures at the R0 level and f is the sensitivity factor of the restoration cost. It could be easily checked that the total cost C = CR + CF has its minimum when the condition is fulfilled. It is natural to assume that the sensitivity factors are reciprocal to the mean-time-to-failure (MTTF) and to the mean-time-to-repair (MTTR) respectively. On the other hand, since the steady-state availability is defined as , then the following formula for the minimum total reliability cost can be obtained: Thus, if availability is high, the minimum cost of failure is, naturally, the cost of keeping the reliability level CR high (so that no failures are likely to occur, or could be fixed in no time).
Figure 1: Simplest cost-reliability optimization model.
Application of foat: Si-on-Si bell labs vlsi package design
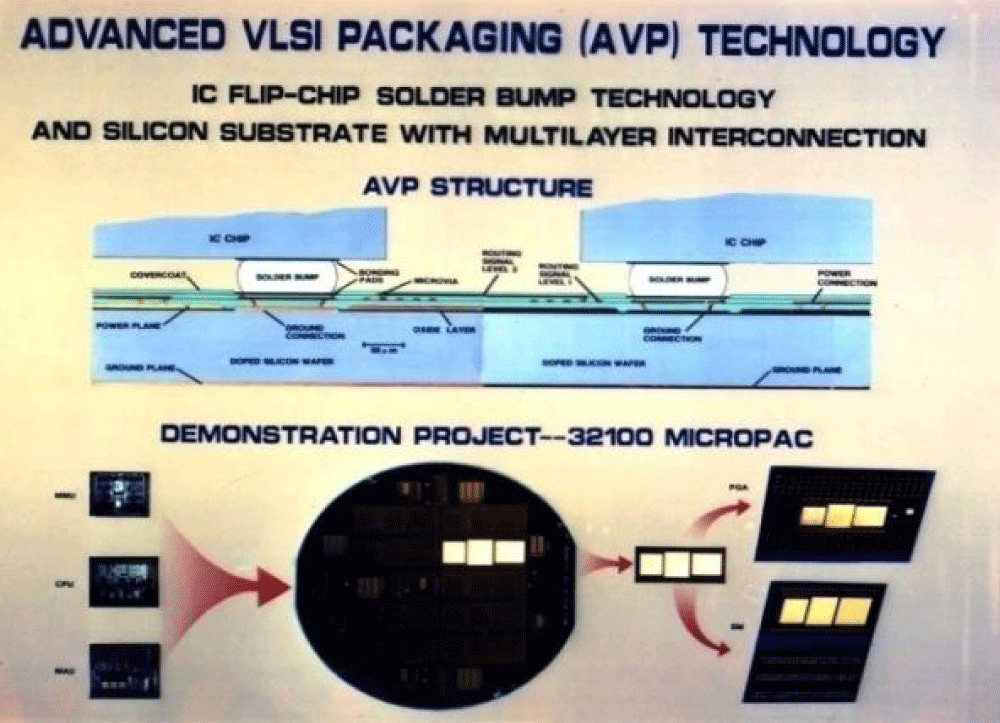
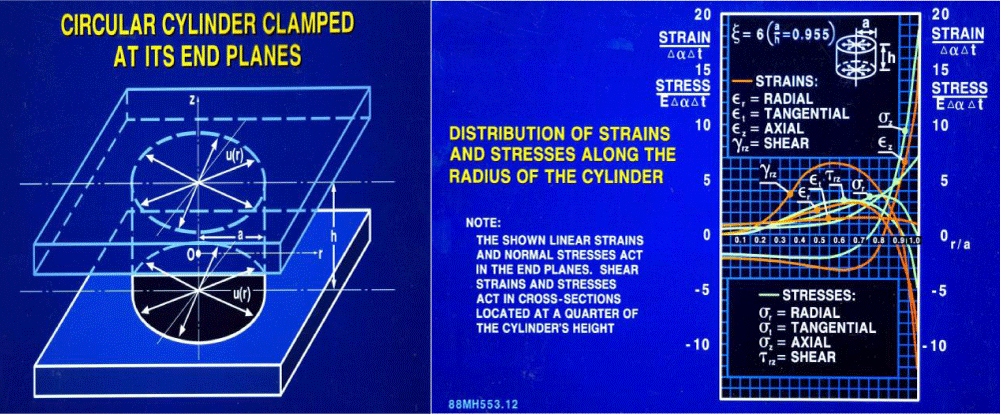
Si-on-Si Bell Labs VLSI package design was the first flip-chip and the first multi-chip module design (Figures 2-4). All the major steps in the PDfR approach were employed in this effort: analytical modeling, confirmed by FEA, of the thermal stresses in the solder joints modeled as short cylinders with elevated stand-off heights (elevated height-to-diameter ratios), FOAT based on temperature cycling, lifetime predictions based on the FOAT data.
Figure 2: Si-on-Si Advanced VLSI Package Design.
Figure 3: In an analytical thermal stress model the solder joints were approximated as short circular cylinders (left sketch), whose plane surfaces were subjected, at low-temperature conditions, to radial tension; the highest stresses and strains acted, however, in the axial direction (right sketch).
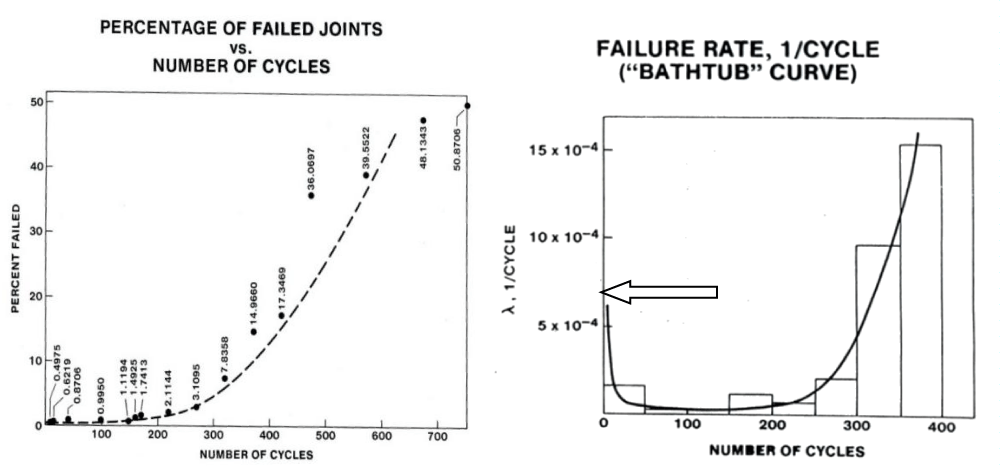
Figure 4: FOAT data (left): tests continued until half of the population failed; the wear-out portion of the experimental bathtub curve (right) is approximately of the same duration as its steady-state portion Experimental BTC for solder joint interconnections in a flip-chip Si-on-Si Bell Labs design. The arrow indicates the initial point of the IMP of the BTC, where the critical time derivative of the nonrandom SFR should be determined. It is the level of this derivative that helps to answer the basic "to BIT or not to BIT" question.
Burn-in testing (bit): To bit or not to bit, that’s the question
BIT [16-23] is, as is known, an accepted practice for detecting and eliminating early failures (“freaks”) in newly fabricated electronic, photonic, MEMS, and MOEMS (optical MEMS) products prior to shipping the “healthy” ones, i.e., those that survived BIT, to the customer(s). This FOAT type of accelerated testing could be based on temperature cycling, elevated (“baking”) temperatures, voltage, current, humidity, random vibrations, light output, etc., or on a physically meaningful combination of these and other stressors. BIT is a costly undertaking. Early failures are avoided, and the infant mortality portion (IMP) of the bathtub curve (BTC) (Figure 4) is supposedly eliminated by conducting an adequate BIT, but this result, if successful, is achieved at the expense of the reduced yield. What is even worse, is that the elevated and durable BIT stressors might not only eliminate undesirable “freaks,” but could cause permanent and unknown damage to the main population of the “healthy” products. The BIT effort should be therefore well understood, thoroughly planned and carefully executed, so that to convert, to an extent possible, this type of testing from a “black box” of a Highly-Accelerated-Life-Testing (HALT) type to a more or less “transparent” one, of the FOAT type.
First of all, it is even unclear whether BIT is always needed at all, not to mention to what extent the current BIT practices are effective and technically and economically adequate. HALT which is currently employed as a suitable BIT vehicle of choice is, as is known, a “black box” that more or less successfully tries “to kill many birds with one stone”. This type of testing is unable to provide any clear and trustworthy information on what BIT actually does, what is happening during and as a result of such testing, and how to effectively eliminate “freaks”, if any, not to mention what could possibly be done to minimize testing time, reduce the BIT cost and duration and to avoid, or at least to minimize, damaging the “healthy” products. Second of all, when HALT is employed to do the BIT job, it is not even easy to determine whether there exists a decreasing failure rate with time at the IMP of the experimental BTC (Figure 4). There is, therefore, an obvious incentive to find and develop ways to better understand and effectively conduct BIT. Ultimately and hopefully, such an understanding might enable even optimizing the BIT process, both from the reliability physics and economics points of view.
Accordingly, in the analysis that follows some important BIT aspects are addressed for a typical E&P product comprised of a large number of mass-produced components. The reliability of these components is usually unknown and their RFR could very well vary in a very broad range, from zero to infinity. Three predictive models are addressed in our analysis: 1) a model based on the analysis of the IMP of the BTC (Figure 4); 2) a model based on the analysis of the RFR of the components that the product of interest is comprised of and 3) a model based on the use of the multi-parametric BAZ constitutive equation. The first model suggests that the time derivative of the BTC’s initial failure rate (at the very beginning of the BTC) can be viewed as a suitable criterion to answer the “to BIT or not to BIT” question for this type of failure-oriented accelerated testing (FOAT). The second model suggests that the above derivative is, in effect, the variance of the above RFR. The third model enables quantifying the BIT effort and outcome by establishing the adequate duration and level of the BIT’s stressor(s). All three predictive models were developed using analytical (“mathematical”) modeling.
Bit model based on the bathtub curve (BTC) analysis
The steady-state mid-portion of the BTC (Figure 4), the “reliability passport” of the manufacturing technology of importance, commences at the left end of the BTC’s IMP. When time progresses, the BTC ordinates reflect the results of the interaction of two irreversible critical processes: the “favorable” statistical (SFR) process that results in a decreasing failure rate with time, and the “unfavorable” physics-of-failure-related (PFR) process associated with the material’s aging and degradation and resulting in an increasing failure rate with time. The first process dominates at the IMP of the BTC and is considered here. As is known, these two processes more or less outweigh each other and result in the steady-state portion of the BTC. The IMP of a typical BTC can be approximated as [47].
(31)
Here λ0 is BTC’s steady-state minimum (failure rate at the end of the IMP and at the beginning of its steady-state portion), λ1 is the initial value of the IMP, t1 is the IMP duration, and the exponent n1 is expressed as where β1 is the IMP “fullness”, defined as the ratio of the area below the BTC to the area (λ1-λ0)t1 of the corresponding rectangular. The exponent n1 changes from zero to one, when the “fullness” β1 changes from zero to 0.5. The following expression for the time derivative of the failure rate λ(t) could be obtained from (31):
(32)
At the initial moment of time (t = 0) this derivative is If this derivative is zero or next-to-zero, this means that the IMP of the BTC is parallel to the horizontal, time, axis. If this is the case, there is no IMP in the BTC at all, and because of that no BIT is needed to eliminate the IMP of the BTC. Clearly, “not to BIT” is the answer in this case to the basic “to BIT or not to BIT” question. What is less obvious is that the same result takes place for . This means that in such a case the IMP of the BTC does exist, but almost clings to the vertical, failure rate, axis, and although the BIT is needed in such a situation, a successful BIT could be very short and could be conducted at a very low level of the applied stressor(s). Physically this means that there are not too many “freaks” in the manufactured population and that those that do exist are characterized by very low activation energies and, because of that, by low probabilities of non-failure. That is why the corresponding required BIT process could be both low-level and short in time. The maximum possible value of the “fullness” β1 is, obviously, β1 = 0.5. This corresponds to the case when the IMP of the BTC is a straight line connecting the initial failure rate, λ1 and the BTC’s steady-state, λ0,values. The time derivative λʹ(0) of the failure rate at the initial moment of time can be obtained from (32) for β1 = 0.5 as and this seems to be the case, when BIT is mostly needed. It will be shown in the next section that this derivative can be determined as the RFR variance of the mass-produced components that the product of interest under BIT is comprised of.
Bit model based on the statistical failure rate (SFR) analysis
It is naturally assumed that the RFR λ of the numerous mass-produced components that the product of interest is comprised of is normally distributed:
(33)
Here is the mean value of the RFR λ and D its variance. Introducing (33) into the formula for the non-random statistical failure rate (SFR) in the BTC and using [100], the expression
(34)
for the non-random, “statistical”, SFR, λst(t) can be obtained. The term “statistical” is used here to distinguish, as has been indicated above, this, “favorable”, failure rate that decreases with time from the “unfavorable” “physical” failure rate (PFR) that is associated with the material’s aging and degradation and increases with time. The PFR is insignificant at the beginning of the IMP of the BTC and is not considered in our analysis. The function
(35)
depends on the dimensionless (“physical”, effective) time
, (36)
and so do the auxiliary function
(37)
and the probability integral (Laplace function)
(38)
The ratio s in (36) can be interpreted as a sort of measure of the level of uncertainty of the RFR in question: this value changes from infinity to zero, when the RFR variance D changes from zero (in the case of a deterministic, non-random, failure rate) to infinity (in the case of an “ideally random” failure rate. In the probability theory (see, e.g., [30]) such a random process is known as “white noise”.
As evident from the formulas (36), the “physical”, effective, time t of the RFR process depends not only on the absolute, chronological, “actual”, real-time τ, but also on the mean value and the variance D of the RFR of the mass-produced components that the product of interest is comprised of. We would like to mention in this connection that it is well known, perhaps, from the times of more than hundred years old Einstein’s relativity theory, that the “physical”, effective, time of an actual physical process or a phenomenon might be different from the chronological, “absolute”, time, and is affected by the attributes and the behavior of the particular physical object, process or a system.
The rate of changing of the “physical” time τ with the change in the “chronological” time t is, as follows from the first formula in (36),
(39)
Thus, the “physical” time changes faster for larger standard deviations of the RFR of the mass-produced components that the product of interest is built of.
Considering (39), the formula (34) yields:
(40)
As one could see from the first formula in (36), the “physical” time τ is zero, when the “chronological” time t is and changes from − ∞ to ∞, when the variance D of the RFR of the mass-produced components that the product of interest is comprised of changes from zero, i.e., when this failure rate is not random, to infinity, when the RFR is “ideally random”, i.e. of a “white noise” type. The calculated values of the function ϕ(τ) expressed by (35) are shown in Table 3. This function changes from 3 zero when the “physical” time τ changes −3 to infinity and the “chronological” time changes from zero to infinity. The tentative derivatives are also calculated in this table.
The expansion (37) can be used to calculate the auxiliary function for large “physical” times τ, exceeding, say, 2.5, and has been indeed employed, when the Table 3 data were computed. The function changes from infinity to zero, when the “physical” time τ changes from − ∞ to ∞. For the “physical” times τ below -2.5, the function is large, and the second term in (35) becomes small compared to the first term. In this case, the function ϕ(τ) is not different from the “physical” time τ itself, with an opposite sign though. As evident from Table 3, the derivative can be put, at the initial moment of time, i.e., at the very beginning of the IMP of the BTC equal to -1.0, and therefore the initial time derivative of the SFR is
(41)
| Table 3: The function ϕ(τ) of the effective (“physical”) time τ and its (also “physical”) time derivative -j¢(t). | ||||||
| t | -3.0 | -2.5 | -2.0 | -1.5 | -1.0 | -0.5 |
| j(t) | 3.0000 | 2.5005 | 2.0052 | 1.5302 | 1.1126 | 0.7890 |
| -j¢(t) | 0.9990 | 0.9906 | 0.9500 | 0.8352 | 0.6472 | 0.4952 |
| t | -0.25 | 0 | 0.25 | 0.5 | 1.0 | 1.5 |
| j(t) | 0.6652 | 0.5642 | 0.4824 | 0.4163 | 0.3194 | 0.2541 |
| s-j¢(t) | 0.4040 | 0.3272 | 0.2644 | 0.1938 | 0.1306 | 0.0922 |
| t | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 |
| j(t) | 0.2080 | 0.1618 | 0.1456 | 0.1300 | 0.1166 | 0.1053 |
| -j¢(t) | 0.0924 | 0.0324 | 0.0312 | 0.0268 | 0.0226 | 0.0190 |
| t | 5.0 | 6.0 | 7.0 | 8.0 | 9.0 | 10.0 |
| j(t) | 0.0958 | 0.0809 | 0.0699 | 0.0615 | 0.0549 | 0.0495 |
| -j¢(t) | 0.0149 | 0.0110 | 0.0084 | 0.0066 | 0.0054 | 0.0044 |
| t | 11.0 | 12.0 | 13.0 | 15.0 | 20.0 | 30.0 |
| j(t) | 0.0451 | 0.0414 | 0.0391 | 0.0332 | 0.0249 | 0.0166 |
| -j¢(t) | 0.0037 | 0.0023 | 0.0030 | 0.0017 | 0.0008 | 0.0003 |
| t | 50.0 | 100.0 | 200.0 | 500.0 | 750.0 | 1000.0 |
| j(t) | 0.0100 | 0.0050 | 0.0025 | 0.0010 | 0 | 0 |
| -j¢(t) | 0.0001 | 2.5E-5 | 5.0E-6 | 2.0E-6 | 0 | 0 |
This fundamental and practically important result explains the physical meaning of the time derivative of the initial failure rate λ1 of the IMP of the BTC: it is the variance (with a sign “minus”, of course) of the RFR of the mass-produced components that the product undergoing BIT is comprised of.
Note that in the simplest case of a uniformly distributed RFR λ, when the probability density distribution function f(λ) is constant, the formula (34) yields:
(42)
In such a case the probability of non-failure becomes time-independent, i.e. constant over the entire operation range: P = exp[-λST (t)t] = e-1 0.3679. This result does not make physical sense, of course, and therefore the normal distribution was accepted in this analysis. Future work should include analyses of the effect of various physically meaningful RFR probability distributions and their effect on the RFR variance. In the analysis carried out in the next section, this variance is accepted as a suitable characteristic (“Figure of merit”) of the propensity of the product under the BIT to the BIT-induced failure.
Bit model based on using the multi-parametric BAZ equation
The BAZ equation [53-67], geared to the highly focused, highly cost-effective, carefully designed, thoroughly conducted, and adequately interpreted FOAT, is an important part of the PDfR concept [38-46] recently suggested for M&P products. This concept is intended to be applied at the stage of the development of new technology for the product of importance. While in commercial E&P reliability engineering, it is the cost-effectiveness and time-to-market that are of major importance, in many other areas of engineering, such as aerospace, military, medical, or long-haul communications, highly reliable operational performance of the M&P products is paramount, and, because of that, has to be quantified to be improved and assured, and because of various inevitable intervening uncertainties in material properties, environmental conditions, states of stress and strain, etc., such a quantification should be preferably done on the probabilistic basis. Application of the PDfR concept enables predicting from the FOAT data, using the BAZ equation, the, in effect, never-zero probability of the field failure of a material, device, package, or system. Then this probability could be made adequate and, if possible and appropriate, even specified for a particular product and application.
The probability of non-failure of an M&P product subjected to BIT, which is, of course, a destructive FOAT for the “freak” population, can be sought, using the BAZ model. Let us show how the appropriate level and duration of the BIT can be determined using the model
(43)
Here D is the variance of the RFR of the mass-produced components that the product of interest is comprised of, I is the measured/monitored signal (such as, e.g., leakage current, whose agreed-upon high enough value I* is considered as an indication of failure; or an elevated electrical resistance, particularly suitable when testing solder joint interconnections; or some other suitable physically meaningful and measurable quantity), t is time, σ is the appropriate “external” stressor, U0 is the stress-free activation energy, T is the absolute temperature, γσ is the stress sensitivity factor and γt is the time/variance sensitivity factor.
There are three unknowns in the expression (30): the product ρ = γt D; the stress-sensitivity factor γσ and the activation energy U0. These unknowns could be determined from a two-step FOAT. At the first step testing should be carried out for two temperatures, T1 and T2, but for the same effective activation energy U = U0-γσσ. Then the relationships
(44)
for the probabilities of non-failure can be obtained. Here t1,2 are the corresponding times and I* is, say, the leakage current at the moment and as indication of failure. Since the numerator U = U0-γσ in the relationships (44) is kept the same, the product ρ = γtD can be found as
(45)
where the notations
(46) are used.
The second step of testing should be conducted at two stress levels σ1 and σ2 and (say, temperatures or voltages). If these stresses are thermal stresses that are determined for the temperatures T1 and T2, they could be evaluated using a suitable thermal stress model. Then
(47)
If, however, the external stress is not thermal stress, then the temperatures at the second step tests should preferably be kept the same. Then the p - value will not affect the factor γσ, which could be found as
(48)
where T is the testing temperature. Finally, the activation energy U0 can be determined as
(49)
The time to failure (TTF) is probability-of-failure dependent and can be determined as TTF = MTTF (-InP), where the MTTF is
(50)
Let, e.g., the following data were obtained at the first step of FOAT: 1) After t1 = 14h of testing at the temperature of T1 = 60 0C = 333 0K, 90% of the tested devices reached the critical level of the leakage current of I* = 3.5µA and, hence, failed, so that the recorded probability of non-failure is P1 = 0.1; the applied stress is elevated voltage σ1 = 380V; and 2) after t2 = 28h of testing at the temperature of T2 = 85 0C = 358 0K. 95% of the samples failed, so that the recorded probability of non-failure is P2 = 0.05. The applied external stress is still elevated voltage of the level σ1 = 380V. Then the formulas (33) yield:
and the product ρ = γtD can be found from the formula (45) as follows:
At the FOAT’s second step one can use, without conducting additional testing, the above information from the first step, its duration and outcome, and let the second step of testing has shown that after t2 = 36,em>h
of testing at the same temperature of T = 60 0C = 333 0K, 98% of the tested samples failed, so that the predicted probability of non-failure is P2 = 0.02. If the stress σ2 is the elevated voltage σ2 = 220V then and the stress-sensitivity factor γσ expressed by (22) isTo make sure that there is no calculation error, the activation energies could be evaluated, for the calculated parameters n1 and n2 and the stresses σ1 and σ2, in two ways:
and
No wonder these values are considerably lower than the activation energies for the “healthy” products. As is known, many manufacturers consider it as a sort of a “rule of thumb” that the level of 0.7eV can be used as an appropriate tentative number for the activation energy of “healthy” electronic products. In this connection it should be indicated that when the BIT process is monitored and the supposedly stress free activation energy U0 is being continuously calculated based on the number of the failed devices, the BIT process should be terminated, when the calculations, based on the FOAT data, indicate that the energy U0 starts to increase: this is an indication that the “freaks”, which are characterized by low activation energies, have been eliminated, and BIT is “invading” the domain of the “healthy” products. Note that the calculated data show also that the activation energy is slightly higher, by about 5% - 8%, for a higher level of stress, i.e., is not completely loading independent. We are going to explain and account for this phenomenon as part of future work.
The MTTF can be determined using the formula (37):
The calculated probability-of-non-failure dependent time-to-failurte (lifetime) TTF = MTTFx (lnP) is 79.2h for P = 0.0075, is 74.5h for P = 0.0100 and is 48.5h for P = 0.050. Clearly, the probabilities of non-failure for a successful BIT, which is, actually, a carefully designed and effectively conducted FOAT, should be low enough. It is clear also that the BIT process should be terminated when the (continuously calculated during testing) probabilities of non-failure start rapidly increasing. How rapidly is “rapidly” should be specified for a particular product, manufacturing technology, and the accepted BIT process?
The following conclusions could be drawn from the above analysis.
- Van Rossum M. The Future of Microelectronics: Evolution or Revolution? Microelectronic Engineering. 1996; 34(1).
- Chatterjee PK, Doering RR. The Future of Microelectronics. Proc IEEE. 1998; 86(1).
- Suhir E. The Future of Microelectronics and Photonics and the Role of Mechanics and Materials. ASME J Electr Packaging (JEP). 1998.
- The Future of Microelectronics. Nature. 2000; 406:1021. https://doi.org/10.1038/35023221
- Suhir E. Microelectronics and Photonics – the Future. Microelectronics Journal. 2000; 31.
- Suhir E. Accelerated Life Testing (ALT) in Microelectronics and Photonics: Its Role, Attributes, Challenges, Pitfalls, and Interaction with Qualification Tests. ASME J Electr Packaging (JEP). 2002; 124(3).
- Duane JT, Collins DH, Jason K, Freels JK, Huzurbazar AV, Warr RL, Brian P, Weaver BP. Accelerated Test Methods for Reliability Prediction. IEEE Trans Aerospace. 1964; 2.
- Nelson WB. Accelerated Testing: Statistical Models. Test Plans and Data Analysis, John Wiley, Hoboken, NJ 1990.
- Matisoff B. Handbook of Electronics Manufacturing Engineering, 3rd ed., Prentice Hall, 1994.
- Ebeling C. An Introduction to Reliability and Maintainability Engineering, McGraw-Hill, 1997.
- Katz A, Pecht M, Suhir E. Accelerated Testing in Microelectronics: Review, Pitfalls and New Developments. Proc of the Int Symp on Microelectronics and Packaging. IMAPS-Israel, 2000.
- Suhir E. Reliability and Accelerated Life Testing. Semiconductor International. 2005. 1.
- Suhir E, Mahajan R. Are Current Qualification Practices Adequate?. Circuit Assembly. 2011.
- Suhir E, Yi S. Accelerated Testing and Predicted Useful Lifetime of Medical Electronics, IMAPS Conf. on Advanced Packaging for Medical Electronics, San-Diego, 2017.
- Suhir E. Making a Viable Electron Device into a Reliable Product: Brief Review, Brief Note. Journal of Electronics & Communications. 1(5).
- Kececioglu D, Sun FB. Burn-in-Testing: Its Quantification and Optimization.; Prentice Hall: Upper Saddle River, NJ, USA, 1997.
- Vollertsen RP, Burn-In, IEEE Int. Integrated Reliability Workshop, USA, 1999.
- Burn-In. MIL-STD-883F: Test Method Standard, Microchips. Method 1015.9; US DoD: Washington, DC, USA, 2004.
- Noel M, Dobbin A, Van Overloop D. Reducing the Cost of Test in Burn-in - An Integrated Approach, Archive: Burn-in and Test, Socket Workshop, Mesa, USA, 2004.
- Ooi MPL, Abu Kassim Z, Demidenko S. Shortening Burn-In Test: Application of HVST Weibull Statistical Analysis. IEEE Transactions. On I&M. 2007; 56(3).
- Ng YH, Low Y, Demidenko SN. Improving Efficiency of IC Burn-In Testing, IEEE Instrumentation and Measurement Technology Conference Proc. 2008.
- Suhir E. To Burn-in, or not to Burn-in: That’s the Question. Aerospace. 2019; 6(3).
- Suhir E. Burn-in Testing (BIT): Is It Always Needed?. IEEE ECTC, Orlando, Fl. 2020.
- Suhir E. Mechanical Behavior and Reliability of Solder Joint Interconnections in Thermally Matched Assemblies. 42-nd ECTC, San-Diego, Calif. 1992.
- Suhir E. Failure-Oriented-Accelerated-Testing (FOAT) and Its Role in Making a Viable IC Package into a Reliable Product, Circuits Assembly. 2013.
- Suhir E. Could Electronics Reliability Be Predicted, Quantified and Assured? Microelectronics Reliability, No. 53, April 15, 2013
- Suhir E, Bensoussan A, Nicolics J, Bechou L. Highly Accelerated Life Testing (HALT), Failure Oriented Accelerated Testing (FOAT), and Their Role in Making a Viable Device into a Reliable Product. 2014 IEEE Aerospace Conference, Big Sky, Montana.
- Suhir E. Failure-Oriented-Accelerated-Testing (FOAT), Boltzmann-Arrhenius-Zhurkov Equation (BAZ) and Their Application in Microelectronics and Photonics Reliability Engineering. Int J of Aeronautical Sci Aerospace Research (IJASAR). 2019; 6(3).
- Suhir E, Ghaffarian R. Electron Device Subjected to Temperature Cycling: Predicted Time-to-Failure. Journal of Electronic Materials. 2019; 48.
- Suhir E. Applied Probability for Engineers and Scientists, McGraw-Hill, New York, 1997.
- Suhir E. Probabilistic Design for Reliability. ChipScale Reviews. 2010; 14(6).
- Suhir E. Remaining Useful Lifetime (RUL): Probabilistic Predictive Model. International Journal of PHM. 2011; 2(2).
- Suhir E, Mahajan R, Lucero A, Bechou L. Probabilistic Design for Reliability (PDfR) and a Novel Approach to Qualification Testing (QT). 2012 IEEE/AIAA Aerospace Conf. Big Sky, Montana, 2012.
- Suhir E. Assuring Aerospace Electronics and Photonics Reliability: What Could and Should Be Done Differently, 2013 IEEE Aerospace Conference, Big Sky, Montana.
- Suhir E. Considering Electronic Product’s Quality Specifications by Application(s), ChipScale Reviews. 2012; 16.
- Suhir E, Probabilistic Design for Reliability of Electronic Materials, Assemblies, Packages and Systems: Attributes, Challenges, Pitfalls, Plenary Lecture, MMCTSE 2017, Cambridge, UK, Feb. 24-26, 2017.
- Suhir E, Ghaffarian R. Solder Material Experiencing Low Temperature Inelastic Thermal Stress and Random Vibration Loading: Predicted Remaining Useful Lifetime, Journal of Materials Science: Materials in Electronics. 2017; 28(4).
- Suhir E. Probabilistic Design for Reliability (PDfR) of Aerospace Instrumentation: Role, Significance, Attributes, Challenges, 5th IEEE Int. Workshop on Metrology for Aerospace (MetroAeroSpace), Rome, Italy, Plenary Lecture, June 20-22, 2018.
- Suhir E. Physics of Failure of an Electronics Product Must Be Quantified to Assure the Product's Reliability, Editorial, Acta Scientific Applied Physics. 2021; 2(1).
- Suhir E. Remaining Useful Lifetime (RUL): Probabilistic Predictive Model, Int. J. of Prognostics-and-Health-Monitoring (PHM). 2011.
- Suhir E. Could Electronics Reliability Be Predicted, Quantified and Assured? Microelectronics Reliability. No. 53, 2013.
- Suhir E. Predictive Modeling is a Powerful Means to Prevent Thermal Stress Failures in Electronics and Photonics. Chip Scale Reviews. 2011; 15(4).
- Suhir E. Electronic Product Qual Specs Should Consider Its Most Likely Application(s), ChipScale Reviews. 2012.
- Suhir E. When Reliability is Imperative, Ability to Quantify It is a Must, IMAPS Advancing Microelectronics. 2013.
- Suhir E. Predicted Reliability of Aerospace Electronics: Application of Two Advanced Probabilistic Techniques, 2013 IEEE Aerospace Conference, Big Sky, Montana, March 2013.
- Suhir E. Statistics and Reliability-Physics-Related Failure Processes. Modern Physics Letters B (MPLB). 2014; 28. 2014
- Suhir E. Analytical Bathtub Curve with Application to Electron Device Reliability. Journal of Materials Science: Materials in Electronics. 2015; 26.
- Suhir E, Bensoussan A. Degradation Related Failure Rate Determined from the Experimental Bathtub Curve. SAE Conf. Seattle, WA, Sept. 22-24, 2015.
- Silverman M. Forty Years of HALT: What Have We Learned? IEEE EPS ASTR 2012 Oct 17-19, Toronto, CA 2012.
- Fundamentals of HALT/HASS Testing (PDF). Keithley Instruments, Inc. Cleveland, Ohio. 2000.
- What is HALT HASS: Performing HALT. Qualmark Corporation. March 1, 2012. Retrieved 10 June 2012.
- Doertenbach N. The Application of Accelerated Testing Methods and Theory (HALT and HASS). QualMark Corporation. 2012-03-01.
- Boltzmann L. About the mechanical meaning of the second law of the theory of heat, scientific treatises, Wiener Berichte. 1866; 53 (in German).
- Boltzmann L. Studies on the balance of living force between moving material points. Vienna reports. 1868; 58 (in German).
- Boltzmann L. The Second Law of Thermodynamics. Populare Schriften, Essay 3, Address to a Formal Meeting of the Imperial Academy of Science. 29 May 1886.
- Arrhenius S. Research on the galvanic conductivity of electrolytes, Doctoral Dissertation, Stockholm, Royal Publishing House. PA Norstedt & Söner. 1884.
- Arrhenius S. On the heat of dissociation and the influence of temperature on the degree of dissociation of the electrolytes. Z. Phys. Chem. 1889; 4.
- Zhurkov SN. “Проблема прочности твёрдых тел” (The Problem of the Strength of Solids), Journal Acad. Nauk SSSR (Bulletin of the USSR Academy of Sciences). 1957; 11.
- Zhurkov SN. Kinetic Concept of the Strength of Solids, Int. J. of Fracture. 1965; 1:4.
- Suhir E, Kang S. Boltzmann-Arrhenius-Zhurkov (BAZ) Model in Physics-of-Materials Problems, Modern Physics Letters B (MPLB). 2013; 27.
- Suhir E, Bechou L, Bensoussan A. Technical Diagnostics in Electronics: Application of Bayes Formula and Boltzmann-Arrhenius-Zhurkov Model.Circuit Assembly. Dec 3, 2012.
- Suhir E, Bensoussan A. Application of Multi-Parametric BAZ Model in Aerospace Optoelectronics. 2014 IEEE Aerospace Conference. Big Sky, Montana. March 2014.
- Suhir E. Three-Step Concept in Modeling Reliability: Boltzmann-Arrhenius-Zhurkov Physics-of-Failure-Based Equation Sandwiched Between Two Statistical Models. Microelectronics Reliability. Oct 2014.
- Suhir E. Static Fatigue Lifetime of Optical Fibers Assessed Using Boltzmann-Arrhenius-Zhurkov (BAZ) Model. Journal of Materials Science: Materials in Electronics. 2017; 28(16).
- Ponomarev A, Suhir E. Predicted Useful Lifetime of Aerospace Electronics Experiencing Ionizing Radiation: Application of BAZ Model. Journal of Aerospace Engineering and Mechanics (JAEM). 2019; 3(1).
- Suhir E. Boltzmann-Arrhenius-Zhurkov Equation and Its Applications in Electronic-and-Photonic Aerospace Materials Reliability-Physics Problems. Int. Journal of Aeronautical Science and Aerospace Research (IJASAR). March 24, 2020.
- Suhir E, Stamenkovic Z. Using Yield to Predict Long-Term Reliability of Integrated Circuit (IC) Devices: Application of Boltzmann-Arrhenius-Zhurkov (BAZ) Model. Solid-State Electronics. Feb. 2020; 164.
- Suhir E. Analytical Modeling in Electronic Packaging Structures: Its Merits, Shortcomings and Interaction with Experimental and Numerical Techniques. ASME Journal of Electronic Packaging. June 1989; 111.
- Suhir E. Modeling of Thermal Stress in Microelectronic and Photonic Structures: Role, Attributes, Challenges and Brief Review. Special Issue, ASME J. Electr. Packaging (JEP). June 2003; 125: 2.
- Suhir E. Analytical Thermal Stress Modeling in Electronic and Photonic Systems. ASME Applied Mechanics Reviews. 2009; 62(4).
- Suhir E. Thermal Stress Failures: Predictive Modeling Explains the Reliability Physics Behind Them. IMAPS Advanced Microelectronics. July/August 2011; 38: 4.
- Suhir E. Could Electronics Reliability Be Predicted, Quantified and Assured? Microelectronics Reliability. July 2013; 53: 7.
- Suhir E. Analytical Modeling Enables Explanation of Paradoxical Situations in the Behavior and Performance of Electronic Materials and Products: Review. Journal of Physical Mathematics. Dec. 2015; 7(1).
- Suhir E. Analytical Modeling Occupies a Special Place in the Modeling Effort. Short Comm. Journal of Physical Mathematics. 2016; 7(1).
- Hall PM. Forces, Moments, and Displacements During Thermal Chamber Cycling of Leadless Ceramic Chip Carriers Soldered to Printed Boards.IEEE CHMT Transactions. Dec 1984; 7(4).
- Suhir E. Mechanical Reliability of Flip-Chip Interconnections in Silicon-on-Silicon Multichip Modules. IEEE Conference on Multichip Modules, IEEE, Santa Cruz. Calif. March 1993.
- Suhir E. Analysis of a Pre-Stressed Bi-Material Accelerated Life Test (ALT) Specimen. Zeitschrift fur Angewandte Mathematik und Mechanik (ZAMM). 2011; 91(5).
- Suhir E. Low-Cycle-Fatigue Failures of Solder Material in Electronics: Analytical Modeling Enables to Predict and Possibly Prevent Them-Review. Journal of Aerospace Engineering and Mechanics. 2018; 2(1).
- Gopalakrishna H, Sinha A, Jordan D, Tamizhmani G. Activation Energy for Solder Bond Degradation: Thermal Cycling of Field-aged Modules at Multiple Upper Temperatures. IEEE 46th Photovoltaic Specialists Conference, PVSC, Chicago, US. June 16-21, 2019.
- Suhir E, Ghaffarian R. Electron Device Subjected to Temperature Cycling: Predicted Time-to-Failure. Journal of Electronic Materials. 2019; 48(2).
- Suhir E. Twist-off Testing of Solder Joint Interconnections. ASME J. Electr. Packaging (JEP). Sept 1989; 111(3).
- Zhang Y, Suhir E, Xu Y, Gu C. Bonding Strength of Carbon Nanofiber Array to its Substrate. JMR. Nov 2006; 21(11).
- Suhir E. Bonded Tri-Material Specimen Subjected to Shear-Off Testing: Predicted Interfacial Stresses. Journal of Aerospace Engineering and Mechanics (JAEM). 2020; 4(1).
- Suhir E. Bi-Material Assembly Subjected to Thermal Stress: Propensity to Delamination Assessed Using Interfacial Compliance Model. Journal of Materials Science: Materials in Electronics. 2016; 27(7).
- Suhir E, Morris J, Wang L, Yi S. Could the Dynamic Strength of a Bonding Material in an Electronic Device Be Assessed from Static Shear-Off Test Data?. Journal of Materials Science: Materials in Electronics. 2016; 27(7).
- Suhir E. Is the Maximum Acceleration an Adequate Criterion of the Dynamic Strength of a Structural Element in an Electronic Product? IEEE CPMT Transactions. Part A. Dec 1997; 20(4).
- Zhou CY, Yu TX, Suhir E. Design of Shock Table Tests to Mimic Real-Life Drop Conditions. IEEE CPMT Transactions. 2009; 32(4).
- Suhir E, Shakouri A. Assembly Bonded at the Ends: Could Thinner and Longer Legs Result in a Lower Thermal Stress in a Thermoelectric Module (TEM) Design? ASME J. Appl. Mech. 2012; 79(6).
- Suhir E, Shangguan D, Bechou L. Predicted Thermal Stresses in a Tri-Material Assembly with Application to Silicon-Based Photovoltaic Module. ASME J. Appl. Mech. March 2013; 80.
- Suhir E, Bechou L, Levrier B. Predicted Size of an Inelastic Zone in a Ball-Grid-Array Assembly. ASME J. Appl. Mech. March 2013; 80.
- Suhir E, Analysis of a Short Beam with Application to Solder Joints: Could Larger Stand-off Heights Relieve Stress? European Journal of Applied Physics (EPJAP). 2015; 71.
- Suhir E, Ghaffarian R, Nicolics J. Could Application of Column-Grid-Array Technology Result in Inelastic-Strain-Free State-of-Stress in Solder Material? Journal of Materials Science: Materials in Electronics. 2015; 26(12).
- Suhir E, Ghaffarian R. Column-Grid-Array (CGA) vs. Ball-Grid-Array (BGA): Board-Level Drop Test and the Expected Dynamic Stress in the Solder Material. Journal of Materials Science: Materials in Electronics. 2016; 27 (11).
- Suhir E, Bechou L. Availability Index and Minimized Reliability Cost. Circuit Assemblies, Feb 2013.
- Suhir E. Axisymmetric Elastic Deformations of a Finite Circular Cylinder with Application to Low Temperature Strains and Stresses in Solder Joints. ASME J. of Appl. Mech. 1989; 56(2).
- Suhir E, Ghaffarian R. Solder Material Experiencing Low Temperature Inelastic Thermal Stress and Random Vibration Loading: Predicted Remaining Useful Lifetime” Journal of Materials Science: Materials in Electronics. 2017; 28(4).
- Suhir E, Poborets B. Solder Glass Attachment in Cerdip/Cerquad Packages: Thermally Induced Stresses and Mechanical Reliability. ASME J Electr. Packaging (JEP). 1990; 112:2.
- Suhir E, Raskin Y, Tunik A. Russian Strength Standards for Commercial Ships. American Bureau of Shipping. 1982
- Suhir E. Probabilistic Methods in Structural Analysis and Vibration of Ships («Вероятностные Методы в Строительной Механике и Вибрации Корабля»), Institute of Naval Architecture, Nikolayev. Ukraine. 1974.
- Gradshteyn IS, Ryzhik IM. Tables of Integrals, Series, and Products. Academic Press. 1980.