More Information
Submitted: February 13, 2023 | Approved: May 23, 2023 | Published: May 24, 2023
How to cite this article: Isaiah O. Probing nuclear equation of state with the cdm3y version of B3y-fetal effective interaction. Int J Phys Res Appl. 2023; 6: 098-114.
DOI: 10.29328/journal.ijpra.1001057
Copyright License: © 2023 Isaiah O. This is an open access article distributed under the Creative Commons Attribution License, which peRmits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Probing nuclear equation of state with the cdm3y version of B3y-fetal effective interaction
Ochala Isaiah*
Department of Physics, Prince Abubakar University, Anyigba, Nigeria
*Address for Correspondence: Ochala Isaiah, Department of Physics, Prince Abubakar University, Anyigba, Nigeria, Email: [email protected]
This paper is a study of the nuclear Equation of State (EOS) of cold nuclear matter with the B3Y-Fetal effective interaction in its CDM3Y density-dependent version within the framework of Hartree-Fock approximation. The well-known saturation properties of both symmetric and asymmetric nuclear matter are well-reproduced in this work. Using the CDM3Y-K approach, this study has evolved a new set of user interactions, some of which are CDB3Y1-, CDB3Y2-, CDB3Y3-, CDB3Y4-, CDB3Y5-, CDB3Y6-Fetal interactions with corresponding incompressibilities K0 = 188, 204, 217,228, 241 and 252 MeV respectively, in excellent agreement with those of the M3Y-Paris and M3Y-Reid effective interactions. For asymmetric nuclear matter, the new set of interactions has produced the symmetry energy Esym = 32.00 MeV with an associated slope parameter L = 55 MeV at a saturation density ρ = 0.17fm−3 and asymmetry parameter δ = 1.00 (pure neutron matter) in good agreement with the standard values obtained from coupled channel analysis of charge exchange reactions, statistical multifragmentation model and terrestrial Nuclear Physics experimental analyses. Furthermore, the new set of interactions has been found to have bright prospects in a nuclear reaction as the real folded potential computed with the CDB3Y6-Fetal interaction within the framework of double folding potential has been found to be good and similar to that of CDB3Y6-Paris whose optical potential has a repulsive direct component.
In contemporary Nuclear Physics, effective interactions have gained wide acceptance as formidable tools for nuclear matter, nuclear structure, and nuclear reaction studies. Of all effective interactions, M3Y interaction, originally derived by fitting Yukawa functions to Brueckner’s G-matrix [1,2], has lately become a popular choice for the study of the properties of finite nuclei and nuclear matter with excellent results. However, to be able to reproduce the saturation of nuclear matter [3] and describe the behavior of finite nuclei [4], the original M3Y interaction had to be modified by introducing a density dependence into it. This modification has followed two approaches, one leading to a set of density-dependent interactions called M3Y-Pn interactions [4,5] and the other has given birth to a set of interactions called, DDM3Yn, BDM3Yn and CDM3Yn interactions [6,7]. With the inclusion of appropriate density dependence, the parameters of these interactions have been adjusted to the data on nuclear structure; some of them have been applied to nuclear reactions [6] alongside nuclear matter and neutron stars [8,9].
The second set of density-dependent interactions (DDM3Yn, BDM3Yn, CDM3Yn) has the density dependence included directly in the finite-range Yukawa terms with the parameters adjusted to reproduce the saturation properties of symmetric nuclear matter [6,7]. This second class of density-dependent M3Y interactions has continued to be applied, with great success to numerous nuclear reactions including folding analyses of nucleon-nucleus, nucleus-nucleus, and charge-exchange reactions [3,6,10]. Thus, it appears that the focus of the M3Y-Pn interactions has been nuclear matter and nuclear structure calculations whereas the focus of the other density-dependent interactions has been nuclear matter and nuclear reactions.
The DDM3Yn, BDM3Yn, and CDM3Yn interactions are based on the original M3Y interaction obtained from the G-matrix elements of the Paris [11] as well as Reid NN potential [1]. These density-dependent interactions have undergone several stages of development and improvement over the years. The DDM3Yn interactions were first to be used [12] followed by the BDM3Yn interactions; and the CDM3Yn interactions came into use as the latest, hybrid versions of the first two versions. The parameters of the DDM3Yn were readjusted by Khoa and Oertzen [12] to get a reasonable limit for negative energies, leading to the reproduction of the empirical values of the saturation binding energy (E/A ≃16 MeV) and density (ρ0 = 0.17fm−3) respectively. The density-dependent M3Y interaction arising from the readjustment was dubbed DDM3Y1; and it gave the incompressibilities K = 170 MeV and 176 MeV with the M3Y-Reid and M3Y-Paris interactions [6,12] respectively. Since the exponential nature of the density dependence made a further readjustment of the parameters for a higher value of K impossible, they used the BDM3Yn interaction to obtain a harder EOS. With different values of β, they fitted the other parameters to the saturation condition as for the DDM3Y1, obtaining the BDM3Y0, BDM3Y1, BDM3Y2, and BDM3Y3 density-dependent versions, which produced the incompressibilities K0 = 190, 232, 353 and 475 MeV, and K0 = 218, 270, 418 and 566 MeV with the M3Y-Reid and M3Y-Paris interactions [12] respectively. These interactions were subsequently used for folding calculations of HI optical potential [6] with insightful results.
Following the approach of Khoa and collaborators [3], the B3Y-Fetal [13] effective interaction has been severally applied to nuclear matter calculations [14-16] within HF approximation and nuclear reactions [17-20] within the framework of the double folding model in the DDM3Yn and BDM3Yn density-dependent versions with excellent results. In Ref. [14], the B3Y-Fetal effective interaction was used in its DDM3Y1, BDM3Y0, BDM3Y1, BDM3Y2, and BDM3Y3 versions for calculations involving symmetric nuclear matter (NM), obtaining the incompressibilities K0 = 176, 196, 235, 351 and 467 MeV respectively. Evidently, these values are in excellent agreement with those of the M3Y-Reid and M3Y-Paris effective interactions.
In order to develop a realistic version of the M3Y effective interaction for consistent use in the mean-field studies of NM, finite nuclei, and nuclear reaction, Khoa, et al. [7] performed a systematic HF study of NM using the M3Y-Paris-based CDM3Yn interactions, which have been used in the folding model studies of nuclear scattering [7,10]. On the basis of their work, the M3Y-Paris interaction is known to have produced the incompressibilities K0 = 188, 204, 217, 228, 241, and 252 MeV corresponding to CDM3Y1, CDM3Y2, CDM3Y3, CDM3Y4, CDM3Y5, and CDM3Y6 respectively [7]. The CDM3Y3, CDM3Y4, CDM3Y5, and CDM3Y6 versions of M3Y-Paris have been variously used for nuclear matter [21], nuclear reaction [7], and astrophysical studies [22]. Similarly, using the CDM3Y-K approach [23], the incompressibilities K0 = 188, 204, 217, 228, 241, and 252 MeV, corresponding to CDM3Y2, CDM3Y3, CDM3Y4, CDM3Y5, and CDM3Y6, were obtained with the M3Y-Reid in its CDM3Y density-dependent version. In the CDM3Y-K approach, the effective interactions (M3Y-Reid and M3Y-Paris) have incompressibility as a common parameter while the other density-dependent parameters are completely different for each effective interaction. This way, the performances of M3Y-Reid and M3Y-Paris effective interactions in this latest hybrid density-dependent version are well-known, whereas the performance of the B3Y-Fetal effective interaction is largely undetermined and unknown. This is the ultimate motivation for this work.
Essentially, this paper is focused on studying the nuclear matter Equation of State (EOS) with the B3Y-Fetal effective in its CDM3Y density-dependent version. The determination of the Equation of State (EOS) of nuclear matter (NM), which has become the main object of numerous nuclear structure and reaction studies lately, is undertaken in this work as a non-relativistic HF study of asymmetric nuclear matter. Using the CDM3Y-K approach, efforts will be made in this study to obtain the versions of the CDM3Y interaction with the B3Y-Fetal effective interaction which can be considered to be the equivalents of CDM3Y1, CDM3Y2, CDM3Y3, CDM3Y4, CDM3Y5 and CDM3Y6 versions of the M3Y-Paris effective interaction. This new parametrization of the density-dependent interaction based on the B3Y-Fetal effective interaction is a novel feature of this research effort. When this goal is achieved, the new set of interactions will be designated for the purpose of identification as CDB3Y1-, CDB3Y2-, CDB3Y3-, CDB3Y4-, CDB3Y5- and CDB3Y6-Fetal interactions respectively. To be able to ascertain the accuracy of computational results, the new parametrizations will be compared with those of the M3Y-Reid and M3Y-Paris effective interactions. In addition, a further step will be taken to apply the new CDM3Y interactions to nuclear reactions to determine and characterize their performance using the M3Y-Reid and M3Y-Paris as standards. Since the use of the new set of interactions could help one trace the sensitivity of refractive scattering data to incompressibility (K-value) in finer detail [7], they will hopefully be used for folding analyses of elastic α-particle scattering data on different targets in subsequent research papers. It is also intended in this work to use computational results to illustrate the hybrid nature of the CDM3Y interaction in clear terms. This is also a relatively new feature of this paper, which is not explicitly discussed in most nuclear matter studies.
The structure of this paper is as follows. In Section 2, simple formulae connecting the CDB3Y-Fetal, CDM3Y-Paris, and CDM3Y-Reid density-dependent parameters with nuclear matter saturation properties, in terms of NN interaction parts, are employed to generate different equations of state with proposed incompressibilities within the non-relativistic Hartree-Fock (HF) scheme. Section 3 is devoted chiefly to the presentation and discussion of the results, and concluding remarks are made in Section 4.
B3Y-fetal in hartree-fock study of nuclear equation of state
The study of nuclear matter-energy, having a functional dependence on the baryonic density, also called the nuclear matter equation of state (EOS) [24], is carried out in this work with CDM3Yn effective interactions whose derivation has resulted from microscopic calculations. The nuclear equation of state plays a significant role in the nuclear ground-state properties, stability of neutron-rich nuclei [25], excitation energies of giant monopole resonances (GMRs), and dynamics of heavy-ion collisions [19]. It also helps in understanding the structure as well as properties of neutron stars such as mass range, mass-radius relationship, crust thickness, cooling rate, and energy released in a supernova explosion [23,26,27]. The two key quantities that characterize the EOS of nuclear matter are the total energy of symmetric NM and symmetry energy [21,22], which correlate strongly with the nuclear incompressibility K and slope parameter of the symmetry energy L at high baryonic densities. The contribution of symmetry energy to the nuclear EOS impacts various phenomena in nuclear astrophysics [28-30], nuclear structure, and nuclear reactions so that its determination is a key objective of contemporary Nuclear Physics, paving the way for understanding the dense matter within neutron stars. But, the density dependence of nuclear symmetry energy has been one of the most uncertain properties of Asymmetric Nuclear Matter (ANM). Many predictions of this property using various many-body theories and interactions diverge quite broadly, especially, at high NM densities. Nonetheless, it is encouraging to note that significant progress has recently been made to constrain the symmetry energy Esym around saturation density, ρ0 [29] based on model analyses of experimental and/or observational data. Also, the M3Y-Pn interactions carefully parametrized by Nakada [8,9] for use in the HF studies of nuclear structure, the D1S and D1N versions of the Gogny interaction [31,32], the Sly4 version of the Skyrme interaction [33] and the CDM3Yn versions of the M3Y-Paris effective interaction have been used in HF study of nuclear matter to understand the density dependence of symmetry energy. Even though these effective NN interactions have given about the same description of the saturation properties of the symmetric NM, the HF results for the asymmetric NM have shown them to be divided into two families associated with two different categories (soft and stiff) of the behavior of the NM symmetry energy at high nucleonic densities. These two families are known now to be representative of the manner in which the nuclear symmetry energy affects the model prediction of different neutron star properties such as the cooling process, gravitational mass, radius, and moment of inertia [21]. Therefore, an attempt is made here to understand and solve the EOS of (symmetric and asymmetric) NM by computing this important quantity alongside its slope parameter, L(ρ) using the B3Y-Fetal-based CDM3Y effective interactions in comparison with the M3Y-Reid and M3Y-Paris effective interactions. This is in anticipation of a future application of the B3Y-Fetal effective interaction to the study of neutron star matter and many other related phenomena in nuclear astrophysics.
In the present work, the nonrelativistic HF scheme is employed to study the EOS of NM at zero temperature, which is characterized by the neutron and proton numbers, N and Z, or neutron-proton asymmetry parameter, δ = (ρn − ρp)/ρ, where neutron and proton densities are ρn = (1+δ)ρ/2 and ρp = (1−δ)ρ/2, respectively.
The total ground-state energy E of the system at the absolute zero temperature in the Hartree-Fock (HF) approximation is given by the sum of the kinetic energy part and potential energy part [21,34-36]:
(1)
where |kτσ〉are plane waves, vD and vEX are the direct and exchange components of a generalized two-body effective NN interaction such as the B3Y-Fetal as well as M3Y-Reid and M3Y-Paris interactions. The factor 1/2 in the total potential energy is meant to avoid double counting of the two-body mutual interactions.
Here, the density dependent NN interaction is the original M3Y interaction supplemented [21] by a realistic density dependence in the form:
(2)
This study is focussed on spin-saturated NM. Therefore, the σ-components of the plane waves are averaged out of the HF calculation (1), so only the isoscalar v00 and isovector v01 components of the central interaction (2) are necessary for the determination of the EOS of NM. Generally, the radial shapes of isoscalar and isovector components of the M3Y-Paris, M3Y-Reid, and B3Y-Fetal interactions are expressed in terms of three Yukawa functions as [1,37]:
(3)
Where the Yukawa strengths and shown in Table 1 are represented in terms of singlet and triplet angular momenta channels [1,19,37].
| Table 1: Yukawa Strengths of the Central Components of B3Y-Fetal [13] and M3Y-Reid [1, 3] M3Y-Paris [3,11] Interactions. | ||||||
| Interaction | i | 1/µi | ||||
| (fm) | (MeV) | (MeV) | (MeV) | (MeV) | ||
| B3Y-Fetal | 1 | 0.25 | 10472.13 | 499.63 | -6197.63 | 365.38 |
| 2 | 0.40 | -2203.11 | -1347.77 | 1277.38 | 576.99 | |
| 3 | 1.414 | 0.0 | -7.8474 | 0.0 | 2.6157 | |
| M3Y-Reid | 1 | 0.25 | 7999.00 | 4631.375 | -4885.5 | -1517.875 |
| 2 | 0.40 | -2134.25 | -1787.125 | 1175.5 | 828.375 | |
| 3 | 1.414 | 0.0 | -7.8474 | 0.0 | 2.6157 | |
| M3Y-Paris | 1 | 0.25 | 11061.625 | -1524.25 | 313.625 | -4118.0 |
| 2 | 0.40 | -2537.5 | -518.75 | 223.5 | 1054.75 | |
| 3 | 1.414 | 0.0 | -7.8474 | 0.0 | 2.6157 | |
For correct reproduction of the saturation properties of NM at the saturation density ρ0 = 0.17fm−3 in the present HF study, the B3Y-Fetal is used alongside the M3Y-Reid and M3Y-Paris interactions in the CDM3Yn (n = 1, 2, 3, 4, 5, 6) density dependence, whose isoscalar G00 and isovector G01 forms are explicitly expressed as [7]:
(4)
This density dependence was originally parametrized by [7] to correctly reproduce the saturation properties of symmetric NM at the saturation density; and several versions of it have been used successfully in the HF studies of NM [38,39] and folding analysis of nucleus-nucleus scattering [40-43]. Using the CDM3Y-K approach [23], various versions of this density dependence are used to generate a number of equations of the state of symmetric NM with incompressibilities K0 ranging from 150 to 300 MeV herein. The parameters C0, α, β and γ of the isoscalar density dependence G00(ρ) are adjusted to reproduce the saturation properties of nuclear matter at density ρ0 = 0.17fm−3 with a binding energy E/A = 16 MeV in this work. The form of isoscalar density dependence G00(ρ) is the same as that of isovector density dependence G01(ρ), but the scaling factor C1 is adjusted in relation to C0 to reproduce the empirical symmetry energy necessary for the construction of a realistic equation of state (EOS) for asymmetric nuclear matter (ANM) within the HF scheme.
Table 2: Parameters of Density Dependence obtained with M3Y-Reid and M3Y-Paris interactions at Equilibrium Using the CDM3Y-K Approach. The results obtained in this work for M3Y-Paris and M3Y-Reid Interactions are in exact agreement with those of [23]. |
||||||||
| CDM3Y-K | Co | M3Y-Paris α |
β | γ | Co | M3Y-Reid α |
β | Γ |
| CDM3Y-150 | 0.4478 | 2.2441 | 4.8600 | 0.1000 | 0.4492 | 2.0257 | 3.9870 | 0.0200 |
| CDM3Y-160 | 0.4335 | 2.3036 | 4.5435 | 0.2000 | 0.4505 | 1.9751 | 3.6805 | 0.2200 |
| CDM3Y-170 | 0.4111 | 2.4349 | 4.2032 | 0.3000 | 0.4517 | 1.9274 | 3.3599 | 0.4400 |
| CDM3Y-180 | 0.3751 | 2.7123 | 3.8318 | 0.4000 | 0.4563 | 1.8599 | 3.0303 | 0.6900 |
| CDM3Y1 | 0.3429 | 3.0232 | 3.5512 | 0.5000 | 0.4590 | 1.8129 | 2.7476 | 0.9100 |
| (K = 188 MeV) CDM3Y-190 | 0.3383 | 3.0616 | 3.4725 | 0.5600 | 0.4645 | 1.7728 | 2.6840 | 0.9700 |
| CDM3Y-200 | 0.3305 | 3.1054 | 3.1835 | 0.8500 | 0.4803 | 1.6478 | 2.3155 | 1.2800 |
| CDM3Y2 | 0.3346 | 3.0357 | 3.0685 | 1.0000 | 0.5617 | 1.2533 | 2.2915 | 1.3499 |
| (K = 204 MeV) CDM3Y-210 | 0.3114 | 3.3020 | 2.8650 | 1.1950 | 0.6897 | 0.8223 | 2.2555 | 1.4199 |
| CDM3Y3 | 0.2985 | 3.4528 | 2.6388 | 1.5000 | 0.8549 | 0.4580 | 2.2363 | 1.4650 |
| (K = 217 MeV) CDM3Y-220 | 0.2963 | 3.4671 | 2.5460 | 1.6401 | 0.9247 | 0.3432 | 2.2170 | 1.4800 |
| CDM3Y-225 | 0.2980 | 3.4151 | 2.3953 | 1.8799 | 1.0421 | 0.1847 | 2.1596 | 1.5000 |
| CDM3Y4 | 0.3052 | 3.2998 | 2.3180 | 2.0000 | 1.1183 | 0.1000 | 2.1286 | 1.5070 |
| (K = 228 MeV) CDM3Y-230 | 0.2961 | 3.4171 | 2.2333 | 2.1501 | 1.1714 | 0.0476 | 2.1097 | 1.5100 |
| CDM3Y-235 | 0.2848 | 3.5656 | 2.0529 | 2.5001 | 1.2960 | -0.0588 | 2.3110 | 1.5200 |
| CDM3Y-240 | 0.2455 | 3.6925 | 1.8686 | 2.9003 | 1.3909 | -0.1284 | 2.4848 | 1.5400 |
| CDM3Y5 | 0.2728 | 3.7367 | 1.8294 | 3.0000 | 1.4061 | -0.1389 | 2.5282 | 1.5450 |
| (K = 241 MeV) CDM3Y-245 | 0.2708 | 3.7465 | 1.6798 | 3.3295 | 1.4777 | -0.1848 | 2.5784 | 1.5600 |
| CDM3Y-250 | 0.2688 | 3.7555 | 1.4795 | 3.7998 | 1.5246 | -0.2151 | 2.8253 | 1.5900 |
| CDM3Y6 | 0.2658 | 3.8033 | 1.4099 | 4.0000 | 1.5468 | -0.2284 | 2.8827 | 1.6000 |
| (K = 252 MeV) CDM3Y-255 | 0.2637 | 3.8203 | 1.2565 | 4.4000 | 1.5955 | -0.2548 | 2.8808 | 1.6100 |
| CDM3Y-260 | 0.2617 | 3.8300 | 1.0034 | 5.0988 | 1.6598 | -0.2884 | 2.9444 | 1.6300 |
| CDM3Y-265 | 0.2580 | 3.8737 | 0.6850 | 6.0980 | 1.6786 | -0.3014 | 3.1686 | 1.6600 |
| CDM3Y-270 | 1.2995 | -0.0374 | 0.6073 | 1.7000 | 1.6855 | -0.3094 | 3.4209 | 1.6900 |
| CDM3Y-280 | 1.5217 | -0.1873 | 2.1054 | 1.7100 | 1.7152 | -0.3317 | 3.8011 | 1.7400 |
| CDM3Y-290 | 1.7114 | -0.2859 | 2.2998 | 1.7200 | 1.7712 | -0.3627 | 3.9982 | 1.7800 |
| CDM3Y-300 | 1.8935 | -0.3622 | 2.394515 | 1.7300 | 1.8037 | -0.3843 | 4.2616 | 1.8200 |
Now, averaging out the spin-dependent terms of (1) from the HF calculations for finite NM, the total NM energy per nucleon for ANM is [23]:
(5)
The first term in equation (5) is the kinetic energy, while and is defined in terms of the first-order spherical Bessel function as = 3j1(x)/x. kFnr, kFpr and kF are the neutron, proton, and total Fermi momenta, respectively, expressed as Taking the partial derivatives of the energy per nucleon, Equation (5), with respect to the nuclear density, the asymmetric NM pressure, P and the incompressibility modulus, K, are respectively obtained as:
(6)
and
(7)
Where
At the saturation density, ρ0, Seif, [23] has shown that the energy per nucleon, the incompressibility, and the saturation condition for the symmetric nuclear matter (SNM), respectively, are:
(8)
(9)
and
(10)
Here,
(11)
and in Equations (9) and (10) denote the first and second derivatives of the density dependence of the isoscalar part of NN interaction with respect to the nuclear density, ρ0. The integrals and depend only on the effective interaction. Consequently, the saturation conditions may be further simplified by substituting the explicit forms of the isoscalar density dependence, G00(ρ0) given by Equation (4), and their derivatives into their respective expressions in Equations (8) - (11). After careful mathematical procedure, the saturation conditions for symmetric NM, in Equations (8) - (12) become:
(12)
Where,
(13)
(14)
(15)
(16)
Di (i = 1 - 4) are constants for the density-independent NN interactions, which are given in terms of the saturation density and energy per nucleon values. For the M3Y-Paris effective interaction, D1 = 0.8806, D2 = −269.81331MeV, D3 = 2.18253fm3 and D4 = −11.53214MeVfm−6. In the case of the M3Y-Reid effective interaction, D1 = 0.90969, D2 = −231.93602MeV, D3 = 1.85104fm3 and D4 =−11.15650MeVfm−6. For the B3Y-Fetal effective interaction, D1 = 0.8717887186, D2 = −234.5976659MeV, D3 = 1.697011283fm3 and D4 = −11.63754722MeVfm−6. These values correspond to UA0(ρ0 = 0.17fm−3) = -16MeV.
Choosing a value for any of the parameters of density dependence, namely β, the other parameters can be determined at a specific saturation incompressibility value. Accordingly, the set of equations for determining the parameters of the density dependence for the CDM3Y interaction is obtained from Equation (12):
(17)
To determine the scaling factor, C1, for the isovector component of the NN interaction, the symmetry energy of the asymmetric nuclear matter has to be calculated using the expression for the EOS of the ANM shown in many theoretical studies [22,44] to be a power series of the form [23]:
(18)
With the contribution of C1 and higher-order terms are shown to be negligible [3,45,46] in the parabolic approximation; Equation (24) becomes
(19)
leading to the definition of symmetry energy as
(20)
Where the symmetry energy Usym is the energy per nucleon required to change the symmetric nuclear matter to pure neutron matter (PNM) and S(ρ) is the symmetry energy coefficient. From Equations (18) and (20), an expression for the symmetry energy coefficient can be written as
(21)
This nuclear symmetry energy (NSE) computed at the nuclear matter saturation density, Usym = S(ρ0) with ρ0 = 0.17fm−3 is well-known in the literature to be 30 ± 2 MeV [3,47], 31 ± 2 MeV, and 31.6 ± 2.7 MeV [30] from numerous many-body calculations and those from the empirical liquid-drop mass formula, analysis of experimental cross-section data in a charge exchange p(6He,6Li*)reaction [34,48] and analyses of the terrestrial Nuclear Physics experiments and astrophysical observations [30,45]. To determine its empirical value, the scaling factor, C1, of the isovector component of the effective interaction is first determined in relation to the scaling factor, C0, of the isoscalar component when the proton-neutron asymmetry, δ = 1.0. In addition to the asymmetry parameter, δ = 1.0, δ = 0.25 is also used for the study of the density dependence of NSE in this paper.
Furthermore, one of the important parameters characterizing nuclear symmetry energy around NM saturation density is the slope parameter whose explicit mathematical representation is [23]:
(22)
This slope parameter is believed to be directly related to the neutron-skin thickness [21,49] of heavy nuclei and the isospin observables in heavy-ion reactions, could give information on neutron stars’ radii [50]; and it is known to have the numerical value L = 58±16 MeV [30,45] and L = 57.7±19 MeV [21,30] based on analyses of the terrestrial Nuclear Physics experiments and astrophysical observations.
The focus of this work has been the study of the EOS of NM (symmetric and asymmetric) with the B3Y-Fetal effective interaction in the CDM3Y density-dependent version along with the M3Y-Reid and M3Y-Paris effective interactions. Herein, the two key quantities characterizing the EOS of NM, explored alongside others, are the energy of symmetric NM and nuclear symmetry energy. This is done using the CDM3Y-K approach [23] in which the value of β of the isoscalar density dependence was chosen with a proposed incompressibility K and the other parameters C0, α, and γ in (18) were determined at the saturation density ρ0 = 0.17fm−3. Used in the CDM3Y density dependence, the resulting B3Y-Fetal-based density-dependent effective interactions are called the CDB3Y-K interactions, generating different equations of state of NM with incompressibilities of symmetric NM ranging from 150 to 300 MeV. Since the performances of M3Y-Reid and M3Y-Paris effective interactions in the CDM3Y density dependence are well-known [7,23], the present HF computation was first carried out with these effective interactions with results that were exact in comparison with those of [23]; and B3Y-Fetal interaction was substituted for them in the same computational procedure with excellent results. The results obtained for symmetric nuclear matter with the three effective interactions are displayed in Tables 2-4. For M3Y-Paris, Tables 2 and 3 shows that the incompressibilities K = 188, 204, 217, 228, 241, and 252 MeV correspond to CDM3Y1-, CDM3Y2-, CDM3Y3-, CDM3Y4-, CDM3Y5- and CDM3Y6-Paris, respectively, in CDM3Yn approach. In the same vein, these versions could be regarded as CDM3Y-K1, CDM3Y-K2, CDM3Y-K3, CDM3Y-K4, CDM3Y-K5, and CDM3Y-K6, respectively, in the CDM3Y-Kn approach; so that the CDM3Yn = CDM3Y-Kn. Applying this reasoning to M3Y-Reid and B3Y- Fetal effective interactions, CDM3Y1-, CDM3Y2-, CDM3Y3-, CDM3Y4-, CDM3Y5- and CDM3Y6-Reid as well as CDB3Y1-, CDB3Y2-, CDB3Y3-, CDB3Y4-, CDB3Y5- and CDB3Y6-Fetal correspond to CDM3Y-K1, CDM3Y-K2, CDM3Y-K3, CDM3Y-K4, CDM3Y-K5, and CDM3Y-K6, respectively, producing the incompressibilities K = 188, 204, 217, 228, 241 and 252 MeV. Here, K1=188 MeV, K2=204 MeV, K3=217 MeV, K4=228 MeV, K5=241 MeV, and K6=252 MeV are the same for M3Y-Paris, M3Y-Reid, and B3Y-Fetal effective interactions, but each of them has a completely different set of parameters of density dependence corresponding to each incompressibility as shown in Table 4. With incompressibility as a common parameter, C0, α, β, and γ have different values for each of the effective interactions. Therefore, for the B3Y-Fetal, using the same set of parameters, CDB3Y1- = CDB3Y-K1, CDB3Y2- = CDB3Y-K2, CDB3Y3- = CDB3Y-K3, CDB3Y4- = CDB3Y-K4, CDB3Y5- = CDB3Y-K5 and CDB3Y6-Fetal = CDB3Y-K6 in this work. In this regard, it is considered appropriate to adopt the CDM3Yn approach to classify the members of this new set of CDM3Y-based interactions for the sake of identification as shown in Figure 1. This criterion for classification applies also to the M3Y-Reid effective interaction in the present work.
| Table 3: Parameters of Density Dependence obtained with B3Y-Fetal and M3Y-Paris interactions at Equilibrium Using the CDM3Y-K Approach. The results obtained in this work for M3Y-ParisInteraction are in exact agreement with those of [23]. | ||||||||
| CDM3Y-K | Co | B3Y-Fetal α | Β | γ | Co | M3Y-Paris a | β | γ |
| CDM3Y-150 | 0.4787 | 1.7081 | 4.2958 | 0.0100 | 0.4478 | 2.2441 | 4.8600 | 0.1000 |
| CDM3Y-160 | 0.4895 | 1.6109 | 4.0086 | 0.2000 | 0.4335 | 2.3036 | 4.5435 | 0.2000 |
| CDM3Y-170 | 0.5029 | 1.5063 | 3.7108 | 0.4000 | 0.4111 | 2.4349 | 4.2032 | 0.3000 |
| CDM3Y-180 | 0.5054 | 1.4594 | 3.3539 | 0.5900 | 0.3751 | 2.7123 | 3.8318 | 0.4000 |
| CDM3Y1 | 0.5086 | 1.4177 | 3.0554 | 0.7600 | 0.3429 | 3.0232 | 3.5512 | 0.5000 |
| (K = 188 MeV) CDM3Y-190 | 0.5158 | 1.3775 | 2.9958 | 0.8100 | 0.3383 | 3.0616 | 3.4725 | 0.5600 |
| CDM3Y-200 | 0.5468 | 1.2137 | 2.6515 | 1.0530 | 0.3305 | 3.1054 | 3.1835 | 0.8500 |
| CDM3Y2 | 0.5641 | 1.1349 | 2.5081 | 1.1500 | 0.3346 | 3.0357 | 3.0685 | 1.0000 |
| (K = 204 MeV) CDM3Y-210 | 0.6183 | 0.9333 | 2.3338 | 1.2800 | 0.3114 | 3.3020 | 2.8650 | 1.1950 |
| CDM3Y3 | 0.7685 | 0.5423 | 2.3200 | 1.3600 | 0.2985 | 3.4528 | 2.6388 | 1.5000 |
| (K = 217 MeV) CDM3Y-220 | 0.8280 | 0.4263 | 2.2902 | 1.3880 | 0.2963 | 3.4671 | 2.5460 | 1.6401 |
| CDM3Y-225 | 0.9408 | 0.2478 | 2.2839 | 1.4200 | 0.2980 | 3.4151 | 2.3953 | 1.8799 |
| CDM3Y4 | 1.0079 | 0.1605 | 2.2708 | 1.4360 | 0.3052 | 3.2998 | 2.3180 | 2.0000 |
| (K = 228 MeV) CDM3Y-230 | 1.0437 | 0.1179 | 2.21510 | 1.4500 | 0.2961 | 3.4171 | 2.2333 | 2.1501 |
| CDM3Y-235 | 1.1716 | -0.0102 | 2.0230 | 1.4630 | 0.2848 | 3.5656 | 2.0529 | 2.5001 |
| CDM3Y-240 | 1.3073 | -0.1183 | 2.0651 | 1.4700 | 0.2455 | 3.6925 | 1.8686 | 2.9003 |
| CDM3Y5 | 1.3141 | -0.1239 | 2.2194 | 1.4800 | 0.2728 | 3.7367 | 1.8294 | 3.0000 |
| (K = 241 MeV) CDM3Y-245 | 1.3813 | -0.1708 | 2.3838 | 1.5000 | 0.2708 | 3.7465 | 1.6798 | 3.3295 |
| CDM3Y-250 | 1.4702 | -0.2258 | 2.4610 | 1.5200 | 0.2688 | 3.7555 | 1.4795 | 3.7998 |
| CDM3Y6 | 1.4978 | -0.2421 | 2.5149 | 1.5300 | 0.2658 | 3.8033 | 1.4099 | 4.0000 |
| (K = 252 MeV) CDM3Y-255 | 1.5518 | -0.2713 | 2.5305 | 1.5400 | 0.2637 | 3.8203 | 1.2565 | 4.4000 |
| CDM3Y-260 | 1.6262 | -0.3091 | 2.5989 | 1.5600 | 0.2617 | 3.8300 | 1.0034 | 5.0988 |
| CDM3Y-265 | 1.6939 | -0.3411 | 2.6676 | 1.5800 | 0.2580 | 3.8737 | 0.6850 | 6.0980 |
| CDM3Y-270 | 1.7553 | -0.3684 | 2.7370 | 1.6000 | 1.2995 | -0.0374 | 0.6073 | 1.7000 |
| CDM3Y-280 | 1.8986 | -0.4239 | 2.7914 | 1.6300 | 1.5217 | -0.1873 | 2.1054 | 1.7100 |
| CDM3Y-290 | 2.0246 | -0.4671 | 2.8614 | 1.6600 | 1.7114 | -0.2859 | 2.2998 | 1.7200 |
| CDM3Y-300 | 2.1349 | -0.5018 | 2.941016 | 1.6900 | 1.8935 | -0.3622 | 2.3945 | 1.7300 |
| Table 3: Parameters of Density Dependence obtained with B3Y-Fetal and M3Y-Paris interactions at Equilibrium Using the CDM3Y-K Approach. The results obtained in this work for M3Y-ParisInteraction are in exact agreement with those of [23]. | ||||||||
| CDM3Y-K | Co | B3Y-Fetal α | Β | γ | Co | M3Y-Paris a | β | γ |
| CDM3Y-150 | 0.4787 | 1.7081 | 4.2958 | 0.0100 | 0.4478 | 2.2441 | 4.8600 | 0.1000 |
| CDM3Y-160 | 0.4895 | 1.6109 | 4.0086 | 0.2000 | 0.4335 | 2.3036 | 4.5435 | 0.2000 |
| CDM3Y-170 | 0.5029 | 1.5063 | 3.7108 | 0.4000 | 0.4111 | 2.4349 | 4.2032 | 0.3000 |
| CDM3Y-180 | 0.5054 | 1.4594 | 3.3539 | 0.5900 | 0.3751 | 2.7123 | 3.8318 | 0.4000 |
| CDM3Y1 | 0.5086 | 1.4177 | 3.0554 | 0.7600 | 0.3429 | 3.0232 | 3.5512 | 0.5000 |
| (K = 188 MeV) CDM3Y-190 | 0.5158 | 1.3775 | 2.9958 | 0.8100 | 0.3383 | 3.0616 | 3.4725 | 0.5600 |
| CDM3Y-200 | 0.5468 | 1.2137 | 2.6515 | 1.0530 | 0.3305 | 3.1054 | 3.1835 | 0.8500 |
| CDM3Y2 | 0.5641 | 1.1349 | 2.5081 | 1.1500 | 0.3346 | 3.0357 | 3.0685 | 1.0000 |
| (K = 204 MeV) CDM3Y-210 | 0.6183 | 0.9333 | 2.3338 | 1.2800 | 0.3114 | 3.3020 | 2.8650 | 1.1950 |
| CDM3Y3 | 0.7685 | 0.5423 | 2.3200 | 1.3600 | 0.2985 | 3.4528 | 2.6388 | 1.5000 |
| (K = 217 MeV) CDM3Y-220 | 0.8280 | 0.4263 | 2.2902 | 1.3880 | 0.2963 | 3.4671 | 2.5460 | 1.6401 |
| CDM3Y-225 | 0.9408 | 0.2478 | 2.2839 | 1.4200 | 0.2980 | 3.4151 | 2.3953 | 1.8799 |
| CDM3Y4 | 1.0079 | 0.1605 | 2.2708 | 1.4360 | 0.3052 | 3.2998 | 2.3180 | 2.0000 |
| (K = 228 MeV) CDM3Y-230 | 1.0437 | 0.1179 | 2.21510 | 1.4500 | 0.2961 | 3.4171 | 2.2333 | 2.1501 |
| CDM3Y-235 | 1.1716 | -0.0102 | 2.0230 | 1.4630 | 0.2848 | 3.5656 | 2.0529 | 2.5001 |
| CDM3Y-240 | 1.3073 | -0.1183 | 2.0651 | 1.4700 | 0.2455 | 3.6925 | 1.8686 | 2.9003 |
| CDM3Y5 | 1.3141 | -0.1239 | 2.2194 | 1.4800 | 0.2728 | 3.7367 | 1.8294 | 3.0000 |
| (K = 241 MeV) CDM3Y-245 | 1.3813 | -0.1708 | 2.3838 | 1.5000 | 0.2708 | 3.7465 | 1.6798 | 3.3295 |
| CDM3Y-250 | 1.4702 | -0.2258 | 2.4610 | 1.5200 | 0.2688 | 3.7555 | 1.4795 | 3.7998 |
| CDM3Y6 | 1.4978 | -0.2421 | 2.5149 | 1.5300 | 0.2658 | 3.8033 | 1.4099 | 4.0000 |
| (K = 252 MeV) CDM3Y-255 | 1.5518 | -0.2713 | 2.5305 | 1.5400 | 0.2637 | 3.8203 | 1.2565 | 4.4000 |
| CDM3Y-260 | 1.6262 | -0.3091 | 2.5989 | 1.5600 | 0.2617 | 3.8300 | 1.0034 | 5.0988 |
| CDM3Y-265 | 1.6939 | -0.3411 | 2.6676 | 1.5800 | 0.2580 | 3.8737 | 0.6850 | 6.0980 |
| CDM3Y-270 | 1.7553 | -0.3684 | 2.7370 | 1.6000 | 1.2995 | -0.0374 | 0.6073 | 1.7000 |
| CDM3Y-280 | 1.8986 | -0.4239 | 2.7914 | 1.6300 | 1.5217 | -0.1873 | 2.1054 | 1.7100 |
| CDM3Y-290 | 2.0246 | -0.4671 | 2.8614 | 1.6600 | 1.7114 | -0.2859 | 2.2998 | 1.7200 |
| CDM3Y-300 | 2.1349 | -0.5018 | 2.941016 | 1.6900 | 1.8935 | -0.3622 | 2.3945 | 1.7300 |
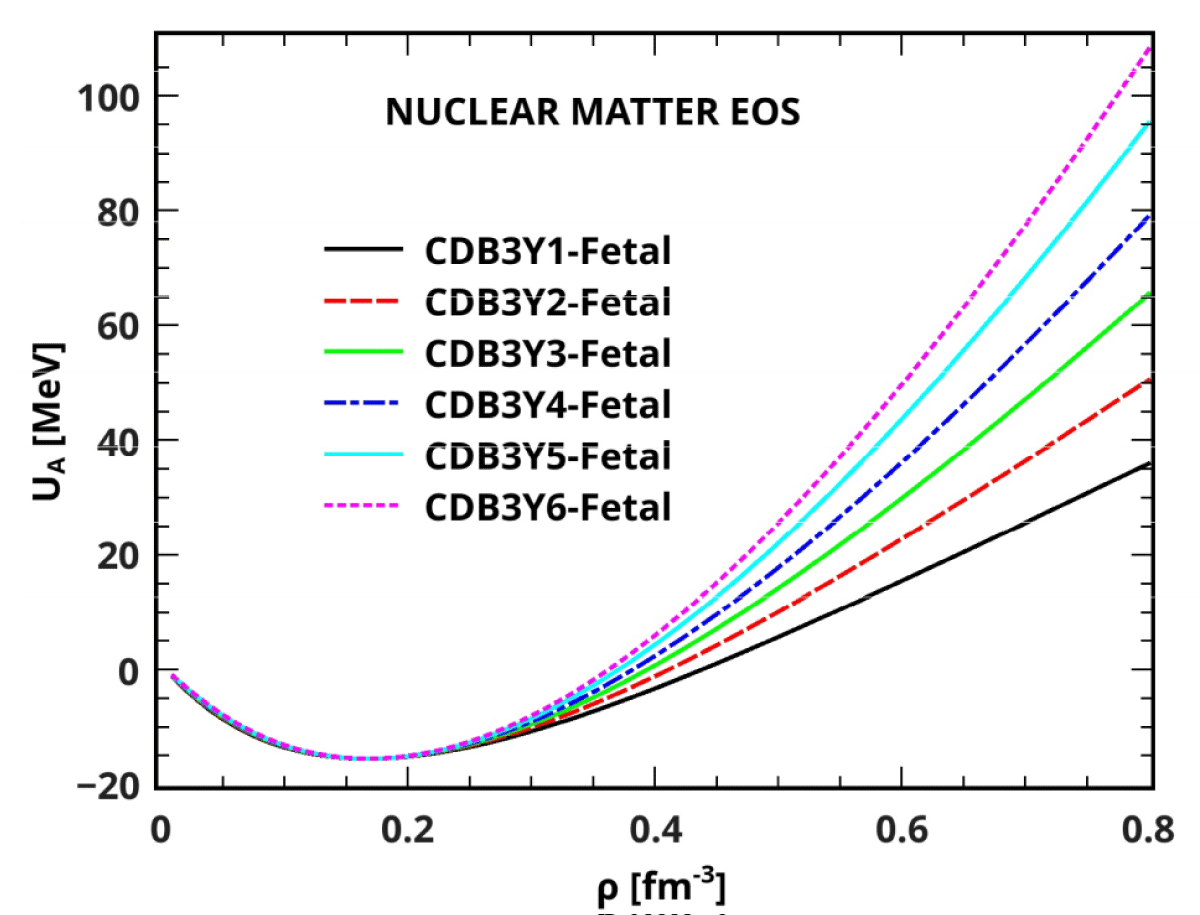
Figure 1: Nuclear Matter Equations of State Obtained with CDB3Y1-, CDB3Y2-, CDB3Y3-, CDB3Y4-, CDB3Y5- and CDB3Y6-Fetal Interactions.
Figure 1 shows the new CDM3Y-K parametrizations of the B3Y-Fetal effective interactions labeled as CDB3Y1-, CDB3Y2-, CDB3Y3-, CDB3Y4-, CDB3Y5- and CDB3Y6-Fetal interactions, corresponding to the incompressibilities K = 188, 204, 217, 228, 241 and 252 MeV respectively. These parameterizations represent the curves of EOS of cold symmetric nuclear matter obtained with the new set of interactions. The saturation of nuclear matter is shown to have been reproduced correctly at density, ρ0 = 0.17fm−3, and binding energy per nucleon UA0 = -16 MeV.
Evidently, all the curves have the same shape and value at the saturation point, demonstrating good agreement with the work presented in [12]. However, as nuclear density increases, the differences in the performances of the interactions are clearly delineated, with the CDB3Y1-Fetal as the weakest and the CDB3Y6-Fetal as the strongest. The CDB3Y5-Fetal (K = 241 MeV) and CDB3Y6-Fetal (K = 252 MeV) interactions, being stronger than the BDB3Y1-Fetal (K = 236 MeV), are the most viable and useful extensions of the application of the B3Y-Fetal effective interaction in nuclear matter and nuclear reaction studies. These versions of the CDM3Y density-dependent interaction obtained from the M3Y-Paris effective interaction (CDM3Y5-Paris and CDM3Y6-Paris) alongside the BDM3Y1-Paris interaction have been found to be the most realistic interactions currently available for folding calculations of α-nucleus and nucleus-nucleus potentials [7]. It is hoped that these versions of CDM3Y interaction derived from the B3Y-Fetal effective interaction in this work will have a parallel performance in nuclear reactions.To study the EOS of asymmetric NM, the density dependence of the isovector part of each effective interaction has been used in conjunction with the isoscalar component with a different strength, C1 = ηC0. The scaling factor, η, was determined through the density dependence of the symmetry energy in (21). With η = 0.62 [3], 0.71 [23], calculations were carried out with B3Y-Fetal and M3Y-Reid effective interactions to reproduce the empirical symmetry energies Usym = 30.66, 31.99 MeV and Usym = 30.61, 32.04 MeV with accompanying slope parameters L = 54, 55 MeV and L = 51, 52 MeV respectively at the neutron-proton asymmetry δ = 1.0. Similarly, with η = 1.0 [3] and 1.1 [23], obtained from the coupled-channel analysis of the charge-exchange reaction p(6He, 6Li*)n [51], the M3Y-Paris interaction produced the symmetry energy Usym = 30.80, 31.99 MeV with an accompanying slope parameter L = 48 and 49 MeV at the asymmetry δ = 1.0. Using the same values of η, B3Y-Fetal, and M3Y-Reid interactions produced Usym = 29.82, 31.10 MeV and Usym = 29.86, 31.24 MeV with accompanying slope parameters L=53, 54 MeV and L = 50, 51 MeV respectively, whereas the M3Y-Paris effective interaction produced Usym = 29.85 and 31.00 MeV with L = 47 and 48 MeV, respectively, at δ = 0.25. These values of symmetry energy have been found to be in good agreement with the empirical standards (30 ± 2 MeV, 31 ± 2 MeV, and 31.6 ± 2.7) established from studies on isospin diffusion [48], GMRs [23], isotopic distribution [52,53], neutron-proton emission ratio [54], relativistic Dirac-Brueckner [27] and variational [49,55] calculations. Obviously, the results obtained with the B3Y-Fetal effective interaction are in good agreement with those of the other effective interactions. Thus, it can be inferred from these results that the range of values of C1 suitable for the reproduction of acceptable symmetry energy for a realistic EOS of ANM, obtained with the CDM3Y-based B3Y-Fetal and M3Y-Reid effective interactions in the present study is C1 = 0.62C0 − 0.71C0, whereas the range for M3Y-Paris is C1 = C0 − 1.1C0. These results also show the strength parameter, C1 of the isovector density dependence of the M3Y-Paris required for a realistic ANM EOS is slightly larger than the value of C1 for the B3Y-Fetal and M3Y-Reid due to their stronger isovector components. The curves of symmetry energy arising from the HF study of the EOS of ANM are shown in Figures 2 and 3 and their salient features are discussed shortly.
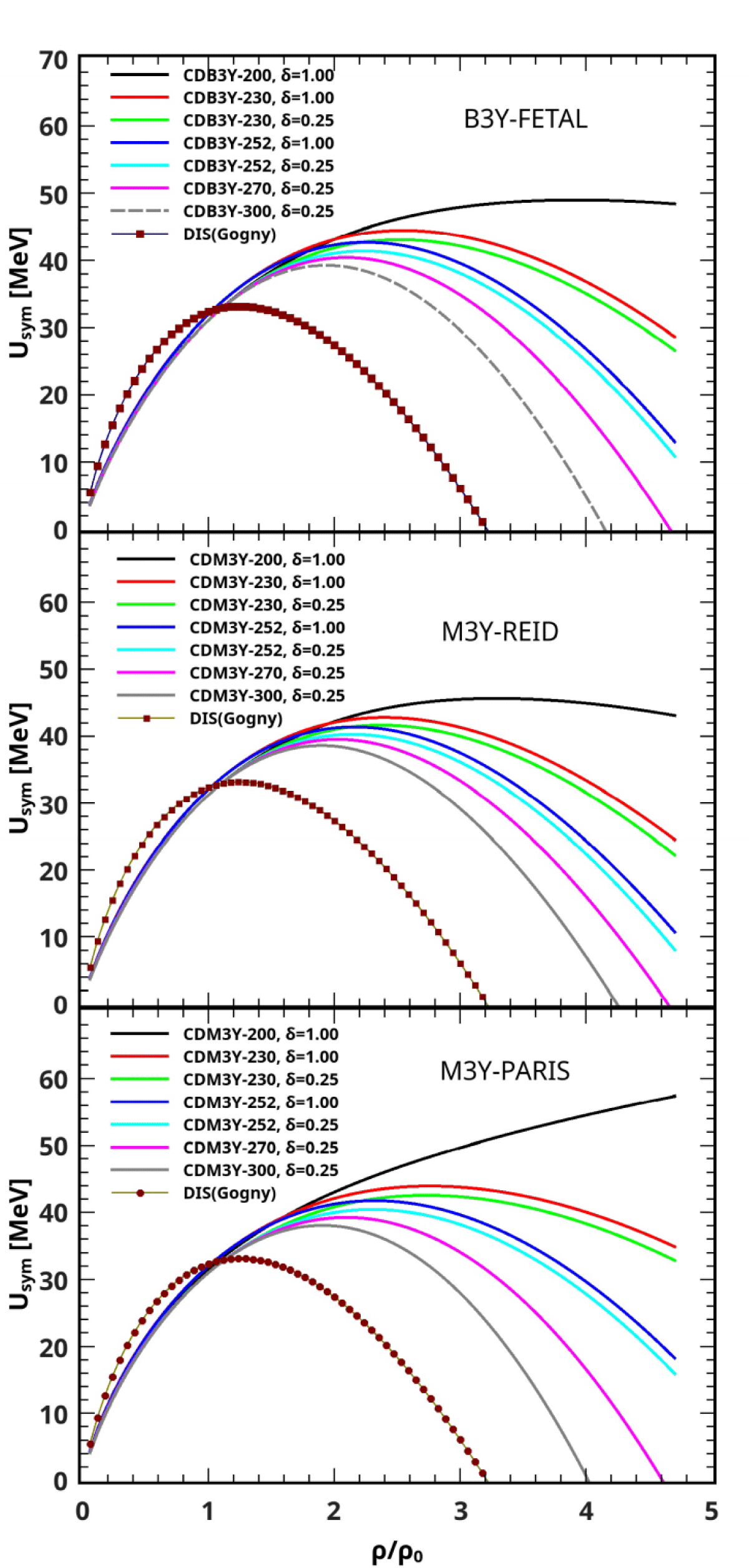
The organization of the equations of state obtained with the CDM3Y interactions in relation to those of the DDM3Y and BDM3Y interactions is well portrayed in Figure 2. For the M3Y-Paris interaction, all the six equations of the state represented by the set of CDM3Yn (n = 1, 6) interactions, constructed originally by Khoa, et al. [7] come entirely between the DDM3Y1 (K = 176) and BDM3Y1 (K = 270 MeV) interactions. Since nuclear reaction studies [6,19] have confirmed cold NM to be governed by soft EOS with K = 220 ± 40 [6], these CDM3Yn interactions have recently been widely used in studies involving NM [22,45] and nuclear reactions [6,41]. For B3Y-Fetal and M3Y-Reid interactions, four of the CDM3Y-based equations of state corresponding to K = 188, 204, 217, and 228 MeV lie between those of DDB3Y1-Fetal (K = 176 MeV), DDM3Y1-Reid (K = 170 MeV) and BDB3Y1-Fetal (K = 235MeV), BDM3Y1-Reid (K = 232 MeV). The remaining two equations of state with incompressibilities K = 241 and 252 MeV are outside of the ranges K = 176 - 235 MeV [14] and K = 170 - 232 MeV [6] associated with B3Y-Fetal and M3Y-Reid interactions respectively. Clearly, these equations of state, represented by CDB3Y5- Fetal, CDB3Y6-Fetal and CDM3Y5-Reid, CDM3Y6-Reid, are useful extensions of the application of the B3Y-Fetal and M3Y-Reid interactions to the description of cold NM within the specified incompressibility range K = 220 ± 40 [6]; and the two of them represent very strong equations of state when compared with the other four. In many HF studies of NM, the CDM3Y6 interaction based on the M3Y-Paris effective interaction has been preferably and variously used by [7,10,40], whereas CDM3Y3, CDM3Y4, and CDM3Y5 have lately been used in nuclear matter studies [21,22,38-40,46] along with the former. Evidently, the CDM3Y6 interaction, which is the strongest of all these interactions, dominates recent nuclear matter studies, proving to be the most relevant. Of all of these interactions, the CDM3Y1 interaction, which represents a very soft nuclear EOS is not used at all in the studies of nuclear matter; and the CDM3Y2 is not also in use for the same reason. Accordingly, the CDB3Y3-, CDB3Y4-, CDB3Y5- and CDB3Y6-Fetal interactions derived in this work are considered to be very useful in nuclear matter and related studies, with the CDB3Y6-Fetal as the strongest and most relevant. Particularly, CDB3Y5- and CDB3Y6-Fetal interactions are stronger than BDB3Y1-Fetal interaction. Since nuclear matter alone is not a sufficient test of the viability of an effective interaction, applying these new interactions to nuclear reaction in this work is imperative. This is shortly discussed.
Furthermore, Figure 2 also illustrates the true nature of the CDM3Y density dependence as a hybrid version of the DDM3Y and BDM3Y density dependences.
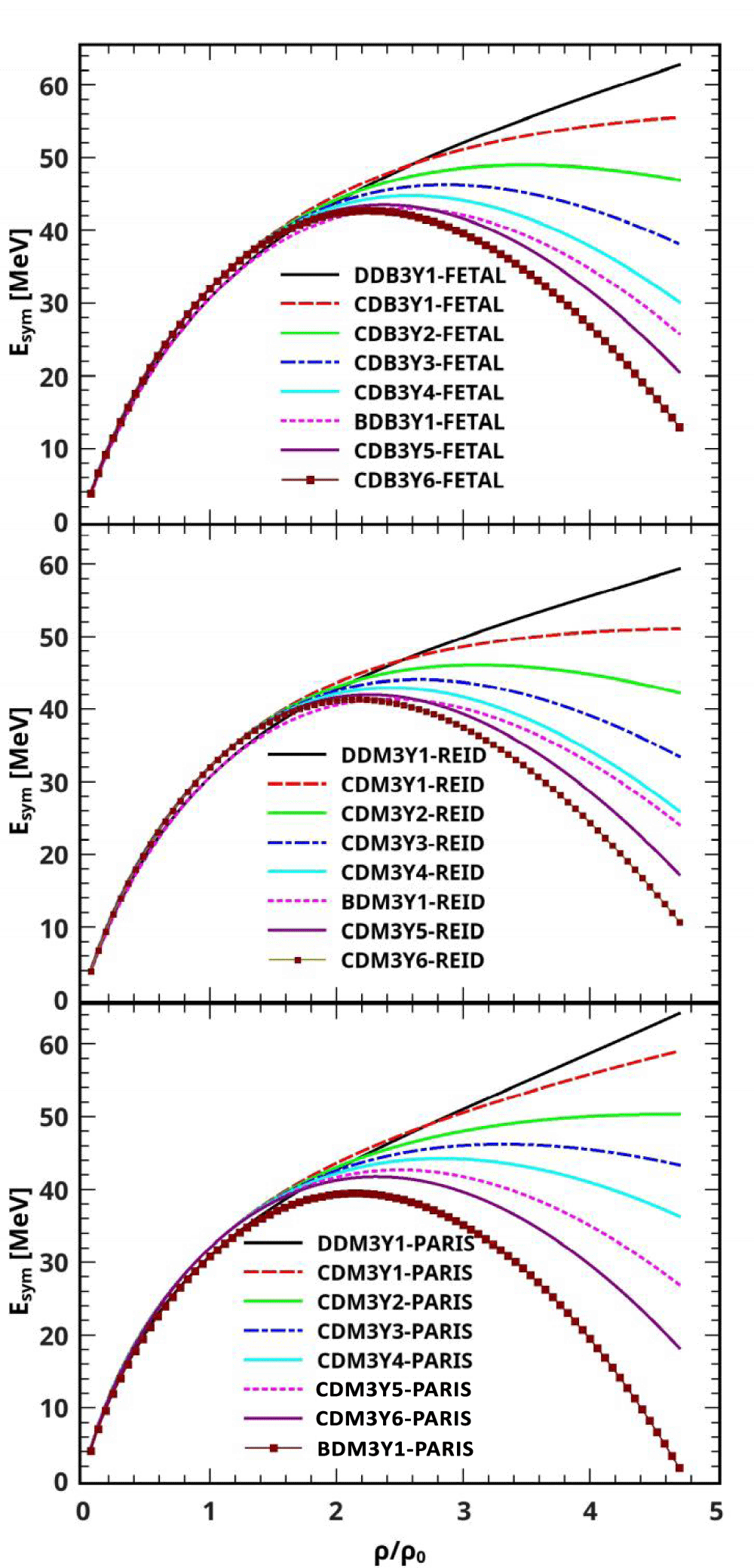
Figure 2: Curves of Symmetry Energy Obtained with CDM3Y1-, CDM3Y2-, CDM3Y3-, CDM3Y4-, CDM3Y5- and CDM3Y6- Versions of B3Y-Fetal (Upper), M3Y-Reid (Middle) and M3Y-Paris (Lower) Effective Interactions at the Asymmetry Parameter, δ = 1.0.
The curves of symmetry energy obtained with the B3Y-Fetal (upper), displayed in this figure, are shown to demonstrate good agreement with those of the M3Y-Reid (middle) and M3Y-Paris (lower). As explained by [3,56], the density dependence of Usym curves based on BDM3Y-type effective interactions (BDM3Y0, BDM3Y1) is such that they reach a maximum at much higher densities and decrease smoothly as density increases, whereas those based on the DDM3Y effective interaction (DDM3Y1) appear to increase in a monotonous manner with increasing density. Accordingly, the curves of Usym obtained from CDM3Y density dependence in Figure 2 are shown to have a density dependence similar to that of DDM3Y1-based curve at lower incompressibilities, but at higher incompressibilities, they have a density dependence that is similar to the Usym curve based on the BDM3Y1 effective interaction. Evidently, the curvature of the CDM3Y-based curves of symmetry energy becomes more sharply defined (soft density dependence of Usym) with increasing incompressibility, portraying the behavior of BDM3Y Usym curves. On the other hand, the curves flatten out (stiff density dependence of Usym) [48,52,57] with decreasing incompressibility, depicting the behavior of DDM3Y Usym curves. This authenticates the hybrid nature of the CDM3Y density dependence.
In Figure 3, the curves of symmetry energy obtained with the CDM3Y-200, CDM3Y-230, CDM3Y-252, CDM3Y-270, and CDM3Y-300 versions of B3Y-Fetal (up-per), M3Y-Reid (middle) and M3Y-Paris (lower) effective interactions at the asymmetry parameters δ = 0.25 and 1.00, are displayed. The density dependence of the symmetry energy is well illustrated up to very high NM densities in this Figure. The density dependence at low NM density is known to have the mathematical representation [23], where µ characterizes the stiffness of the symmetry energy. Using this expression at low NM densities ρ ≤ 1.5ρ0, the various CDM3Y-K versions of the B3Y-Fetal have produced a stiffness value of about 0.63, while those of the M3Y-Reid and M3Y-Paris interactions have produced 0.60 and 0.58 respectively. Compared with previous work, these values of stiffness, computed in this work, are in good agreement with 0.62 and 0.55 respectively obtained with the CDM3Y-K versions of M3Y-Reid and M3Y-Paris interactions [23] as well as the range µ = 0.55 − 0.79 obtained from other independent studies [27,49,52]. Figure 3 also shows a strong correlation between the symmetry energy and nuclear incompressibility value (K-value) at high nuclear density. The symmetry energy of dense NM for which ρ ≤ 2.0ρ0 predicted by the various CDM3Y-K parametrizations of the three effective interactions is observed to grow increasingly softer with increasing incompressibility value, with the CDM3Y-200 Usym curve having a stiff appearance while the CDM3Y-300 curve has a very soft form. In accordance with the results of [23], the CDM3Y-K Usym curves reach their maximum values in the nuclear density range from 2ρ0 to 4.1ρ0 and then decrease smoothly with increasing nuclear density to negative values at different points. In comparison, the curve produced by the Gogny force (DIS) is much softer at high nuclear matter density than the curves produced by the CDM3Y-K curves, attaining its maximum value at about 1.2ρ0 and decreasing to negative values at 3.2ρ0.
Figure 3: Curves of Symmetry Energy Obtained with CDM3Y-200, CDM3Y-230, CDM3Y-252, CDM3Y-270 and CDM3Y-300 Versions of B3Y-Fetal (Upper), M3Y-Reid (Middle) and M3Y-Paris (Lower) Effective Interactions at the Asymmetry Parameters, δ = 1.0 and δ = 0.25.
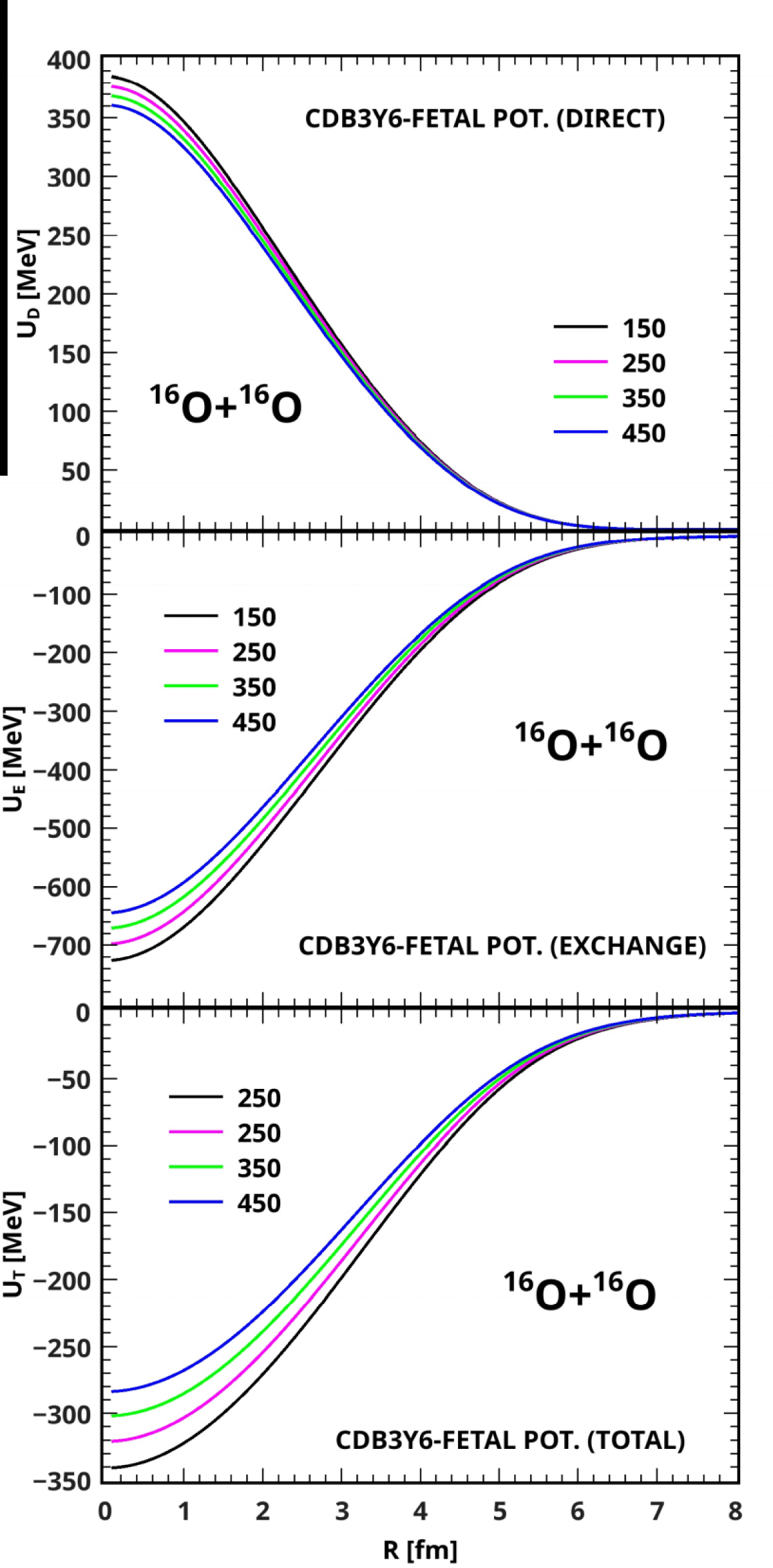
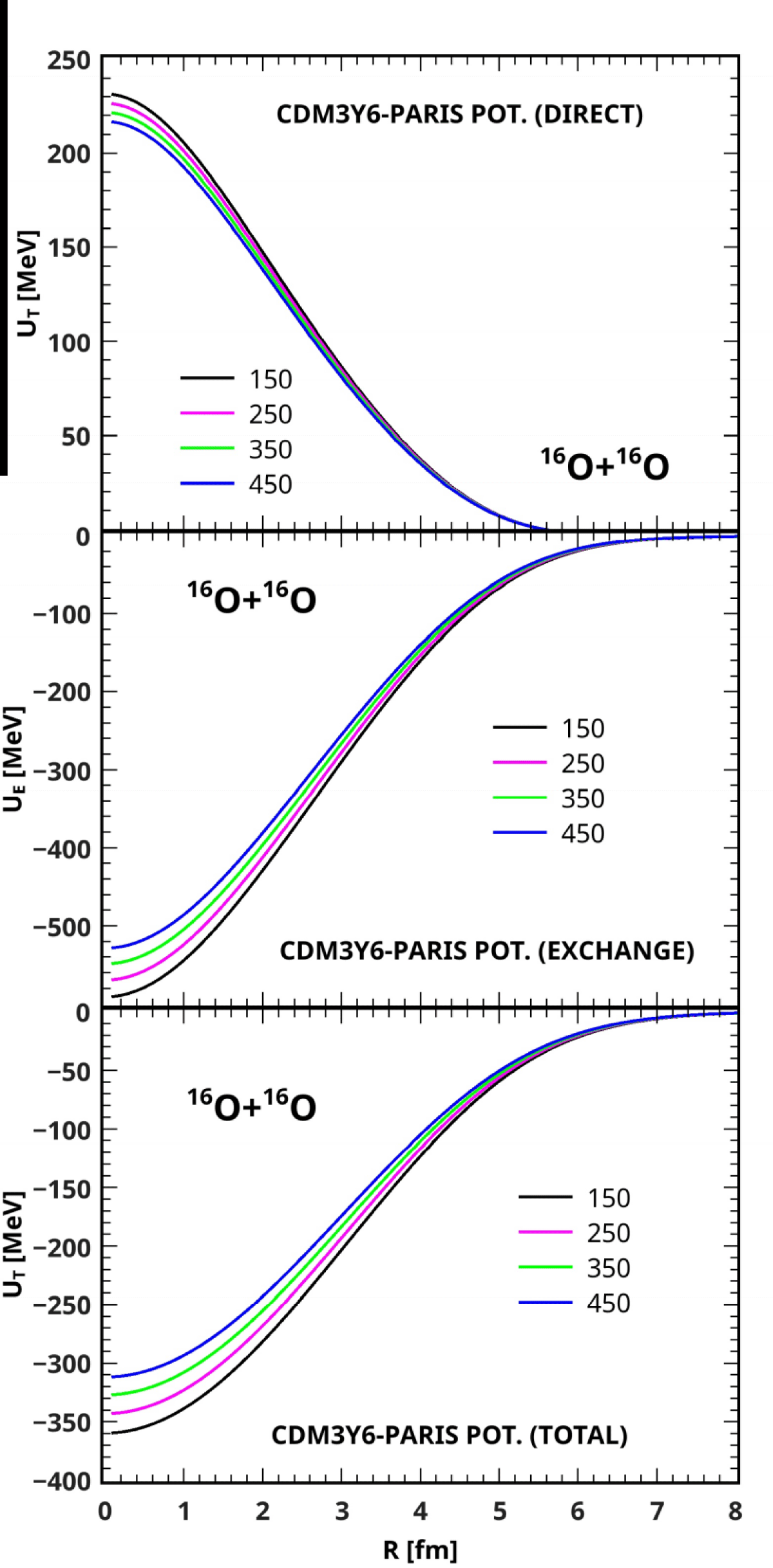
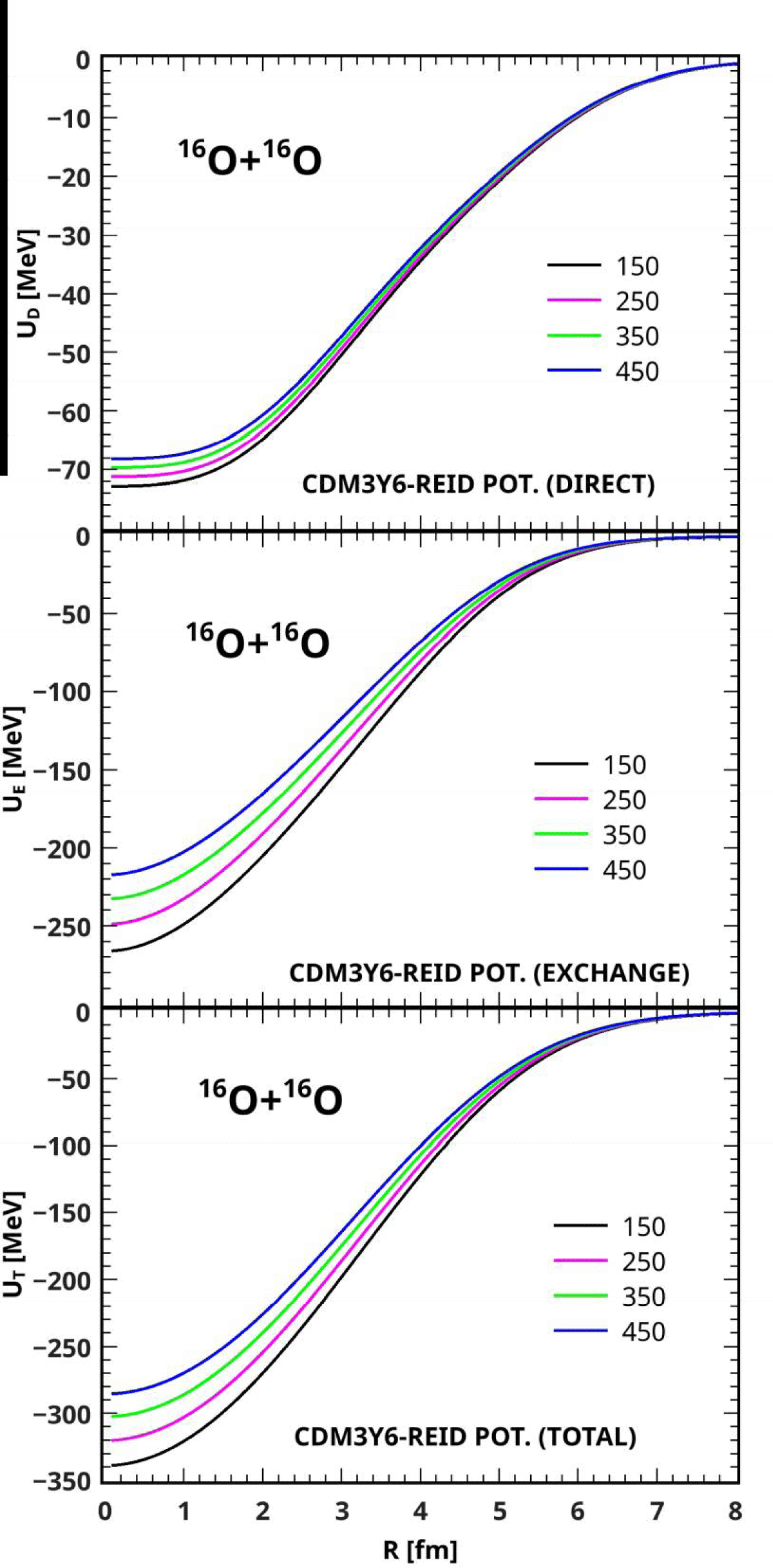
In a bid to determine the possibility of successful application of the new CDM3Y- interactions, derived from the B3Y-Fetal and M3Y-Reid interactions, to nuclear reaction, the CDB3Y6-Fetal has been used along with those of the M3Y-Reid and M3Y-Paris effective interactions within the framework of the optical model to construct a nucleus-nucleus optical potential involving 16O + 16O nuclear system at the incident energies of 150, 250, 350 and 450 MeV. A careful comparison of the real folded potentials obtained from the three effective interactions has shown the CDB3Y6-Fetal (Figure 4) and CDM3Y6-Paris (Figure 5) folded potentials to be similar in the sense that both of them have repulsive direct components, while the CDM3Y6-Reid (Figure 6) potential has an attractive direct component as shown in [19,20]. It is also noteworthy to see that the potentials (UD, UEX, and UT) based on the B3Y-Fetal are in good agreement with the potentials derived from the M3Y-Reid and M3Y-Paris effective interactions in terms of magnitude, shape, and trend. In terms of magnitude, results of folding calculations have shown the largest values of CDB3Y6-Fetal potential at smaller inter-nuclear distances to be -340.7, -320.9, -301.9, and -283.7 MeV at the incident energies of 150, 250, 350 and 450 MeV respectively; the largest values of CDM3Y6-Reid potential are -338.9, -320.2, -302.4 and -285.5 MeV; and the CDM3Y6-Paris has -359.6, -342.9, -327.0 and -311.7 MeV respectively at the same incident energies. Here, the CDM3Y6-Paris has a greater performance strength than the CDB3Y6-Fetal and CDM3Y6-Reid potentials. The trend of performance strength exhibited by the last two potentials in which the CDB3Y6-Fetal is stronger at lower incident energies than CDM3Y6-Reid potential has been explained in [19,20] to be due to the dominating effect of the direct component on the exchange component of CDB3Y6-Fetal, making its total real folded potential more rapidly repulsive than the CDM3Y6-Reid potential as the incident energy increases. On the whole, the agreement demonstrated by the CDB3Y6-Fetal with CDM3Y6-Paris and CDM3Y6-Reid potentials gives hope that the new set of B3Y-Fetal-based CDM3Y interactions will do well in nuclear reactions and astrophysical studies.
Figure 4: Direct (upper part) and Exchange (Middle) Contributions to the Total Folded CDB3Y6-FETAL Potential (Lower Part) for the 16O + 16O System at Incident Energies from 9 to 28 MeV/Nucleon.
Figure 5: Direct (upper part) and Exchange (Middle) Contributions to the Total Folded CDM3Y6-PARIS Potential (Lower Part) for the 16O + 16O System at Incident Energies from 9 to 28 MeV/Nucleon.
Figure 6: Direct (upper part) and Exchange (Middle) Contributions to the Total Folded CDM3Y6-REID Potential (Lower Part) for the 16O + 16O System at Incident Energies from 9 to 28 MeV/Nucleon.
This study has been focussed on probing the equation of the state of nuclear matter with the B3Y-Fetal in its CDM3Y density-dependent version. Using the CDM3Y-K approach, a number of equations of the state represented by a range of incompressible- entities from K = 150 to 300 MeV have been derived in this work. Among these, the equivalents of CDM3Y1-, CDM3Y2-, CDM3Y3-, CDM3Y4-, CDM3Y5- and CDM3Y6-Paris interactions, corresponding to the incompressibilities K = 188, 204, 217, 228, 241, and 252 MeV, derived herein with the B3Y-Fetal effective interaction are called CDB3Y1-, CDB3Y2-, CDB3Y3-, CDB3Y4-, CDB3Y5- and CDB3Y6-Fetal interactions respectively. Of all of these interactions, the CDB3Y5- and CDB3Y6-Fetal interactions, being stronger than the BDB3Y1-Fetal interaction, have been found to be the most viable and useful extensions of the application of the B3Y-Fetal interaction to the description of cold NM within the specified incompressibility range K = 220 ± 40 [6]. This is a major finding of this research. A further step taken to confirm the viability of this new set of B3Y-Fetal-based CDM3Yn interactions by applying the strongest of them, the CDB3Y6-Fetal, to a nuclear reaction within the framework of the optical model has been interestingly successful. Accordingly, the optical potentials derived from the B3Y-Fetal at the incident energies of 150, 250, 350, and 450 MeV have been found to be similar to those based on the M3Y-Paris effective interaction in magnitude, shape, and trend. This is the second major finding of this research, which is a purveyor of hope that the new interactions are reliable computational tools in nuclear reactions. In all cases of comparison, the predictions of nuclear EOS obtained with the B3Y-Fetal here are in excellent agreement with those of the M3Y-Reid and M3Y-Paris effective interactions. This implies that the new set of B3Y-Fetal-based CDM3Yn interactions can be applied to all nuclear physics and astrophysical phenomena with immense success. Subsequently, these new interactions, most especially the CDB3Y5- and CDB3Y6-Fetal interactions will be used for detailed optical model analyses of elastic α-scattering data on targets ranging from 12C to 208Pb nuclei like their CDM3Y-Paris counterparts [7].
Profuse thanks to Professor Dao Tien Khoa of the Institute for Nuclear Science and Technology, Vietnam for his eye-opening and path-charting work on nuclear matter as well as helpful, private communication. Grateful mention is also made of Professor Waala Seif of Cairo University, Egypt, whose work on nuclear matter has been great succor in this study.
- Bertsch G, Borsowicz J, McManus H, Love WG. Interac- tions for Inelastic Scattering Derived from Realistic Potentials. Nuclear Physics A. 1977; 284:399-419.
- Wong SM. Introductory Nuclear Physics. Toronto: Prentice-Hall International, Inc. 1990.
- Khoa DT, Oertzen VW. Oglobin. Study of the Equation of State for Asymmetric Nuclear Matter and Interaction Potential between Neutron-Rich Nuclei Using the Density-Dependent M3Y Interaction. Nu- clear Physics A. 1996; 602:98-132.
- Nakada H. Hartree-Fock Approach to Nuclear Matter and Finite Nuclei with M3Y-type Nucleon-Nucleon Interactions. Physical Review C. 2003; 68(014316):42-59.
- Nakada H. Mean-field Approach to Nuclear Structure with Semi-Realistic Nucleon-Nucleon Interactions. Physical Review C. 2010a ; 78(054301):67-87.
- Khoa DT, von Oertzen W, Bohlen HG. Double-folding model for heavy-ion optical potential: Revised and applied to study 12C and 16O elastic scattering. Phys Rev C Nucl Phys. 1994 Mar;49(3):1652-1668. doi: 10.1103/physrevc.49.1652. PMID: 9969388.
- Khoa DT, Satchler GR, Oertzen WV. Nuclear Incompress- ibility and Density Dependent NN Interactions in the Folding Model for Nucleus Potentials. Physical Review C. 1997; 56(2):954-969.
- Nakada H. Modified Parameter-Sets of M3Y-type Semi-Realistic Nucleon-Nucleon Interactions for Nuclear Structure Studies Physical Re- view C. 2010; 81(027301):42-59.
- Nakada H. Semi-Realistic Nucleon-Nucleon Interactions with Im- proved Neutron Matter Properties. Physical Review C. 2013; 87(1):14-38.
- Khoa DT, Oertzen VW, Bohlen HG, Ohkubo S. Nuclear Rainbow Scattering and Nucleus-Nucleus Potential. Journal of Physics: Nuclear Physics. 2007; 34R111(3):1-65.
- Anantaraman N, Toki H, Bertsch GF. An Effective Inter- action for Inelastic Scattering Derived from the Paris Potential.Nuclear Physics A. 1983; 398:269-278.
- Khoa DT, Oertzen VW. A Nuclear Matter Study Using the Density-Dependent M3Y Interaction. Physics Letters B. 1993; 304:8-16.
- Fiase JO, Devan KRS, Hosaka A. Mass Dependence of M3Y-Type Interactions and the Effects of Tensor Correlations. Physical Review C. 2002; 66(014004):1-9.
- Ochala I, Fiase JO. Symmetric Nuclear Matter Calcula- tions - A Variational Approach. Physical Review C. 2018; 98(064001):1-8. DOI:10.1103/PhysRevC.98.064001.
- Ochala I, Gbaorun F, Bamikole JA, Fiase JO. A micro- scopic Study of Nuclear Symmetry Energy with an Effective Interaction Derived from Variational Calculations. International Research Journal of Pure and Applied Physics. 2019; 6(2):22-33.
- Ochala I, Fiase JO, Momoh HO, Okeme IC. The Mass-Dependent Effective Interactions as Applied to Nuclear Matter. Nigerian Journal of Physics. 2020; 29(1):209-219.
- Ochala I, Terver D, Fiase JO. A Study of 12C +12 C Nuclear Reaction using a New M3Y-Type Effective Interaction. Inter- national Journal of Physics Research and Applications. 2020; 3:133-142. DOI:10.29328/journal. ijpra.1001031
- Ochala I. Optical Model Analyses of Elastic Scattering of 16O +12 C . International Journal of Applied Mathematics and Theoreti- cal Physics. 2021; 7(1):1-9. DOI: 10.11648/j.ijpra.20210701.11
- Ochala I, Fiase JO. B3Y-Fetal Effective Interaction in the Folding Analysis of Elastic Scattering of 16O +16 O. Nuclear Science and Techniques. 2021; 32(81):1-14. DOI: 10.1007/s41365-021-00920-z.
- Ochala I, Fiase JO, Obaje VO, Sule VI. The Mass- Dependent Effective Interactions Applied to Nuclear Reactions. Aus- tralian Journal of Basic and Applied Sciences. 2021; 15(10):1-12. DOI: 10.22587/ajbas.2021.15.10.1.
- Khoa NHD, Tan NT, Khoa DT. Spin Symmetry Energy and Equation of State of spin-Polarized Neutron Star Matter. Physical Review C. 2022; 105(065802):1-12.
- Tan NT, Khoa DT, Loan DT. Equation of State of Asymmetric Nuclear Matter and the Tidal Deformability of Neutron Star. Eur. Phys. J. A. 2021; 57:153.
- Seif WM. Nuclear Matter Equation of State Using Density- Dependent M3Y Nucleon-Nucleon Interactions. J. Phys. G.: Nucl. Part. Phys. 2011; 38(035102):1-21.
- Gulminelli F. Neutron-Rich Nuclei and the Equation of State of Stellar Matter. Physica Scripta. 2013; 152(014009):1-10.
- Todd BG, Piekarewicz J. Relativistic Mean-Field Study of Neutron-Rich Nuclei. 2003. DOI: 10.1103/PhysRevC.67.044317.
- Ban SF, Li J, Zhang SQ, Jia HY, Sang JP, Meng J. Density Dependencies of Interaction Strengths and their Influ- ences on Nuclear Matter and Neutron Stars in the Relativistic Mean Field Theory. Physical Review C. 2004; 69(4):28-55.
- Dalen V, ENE, Fuchs C, Faessler A. The Relativis- tic Dirac-Brueckner Approach to Asymmetric Nuclear Matter. Nuclear Physics A. 2004; 744:227-248.
- Trautman W. Collective Motion and the Asymmetric Matter Equation of State. Discoveries at the FFrontiers of Science. Book Chap- ter. 2020; 213-223.
- Tsang MB, Stone JR, Camera F, Danielewicz P, Gandolfi S, Hebeler K, Horowitz CJ, Lee J, Lynch WG, Kohley Z, Lemmon R, Mo¨ller P, Murakami T, Riordan S, Roca-Maza X, Sammarruca F, Steiner AW, Vidan˜a I, Yennello, SJ. Constraints on the Symmetry Energy and Neutron Skins from Experiments and Theory. Physical Review C. 2012; 86(1):015803.
- Li BA, Han X. Constraining the Neutron-Proton Effective Mass Splitting using empirical Constraints on the Density Dependence of Nuclear Symmetry Energy Around Normal Density. Physics Letters B. 2013; 727:276-281.
- Berger JF, Girod M, Gogny D. Time-Dependent Quan- tum Collective Dynamics Applied to Nuclear Fission. Computer Physics Communications. 1991; 763(1-3): 365-374.
- Chappert F, Girod M, Hilaire S. Towards a New Gogny Force Parameterization: Impact of the Neutron Matter Equation of State. Physics Letters B. 2008; 668 (5):420-424.
- Chabanat E, Bonche P, Haensel P, Meyer J, Schaeffer R A. Skyrme Parametrization from Subnuclear to Neutron Star Densities 1998; Part II. Nuclei far from Stabilities. Nuclear Physics A. 635(1-2): 231-256.
- Than H S, Khoa DT, Giai NV. Neutron Star cooling: A Challenge to the Nuclear Mean Field. Physical Review C. 2009; 80: 064312.
- Sharma ML, Matiasi CO, Khanna KM. Nuclear Mat- ter Calculations with a Density Dependent Effective Nucleon-Nucleon Interaction. Indian Journal of Pure and Applied Physics. 2000; 38: 625 - 634.
- Mansour HMM, Ramadan KA, Hammad M. Proper- ties of Nuclear and Neutron Matter Using D1 Gogny Force. Ukr J Phys. 2004; 49(8): 756-762.
- Than HS. Microscopic Description of Nuclear Structure and Nu- clear Reactions. Unpublished PhD Thesis. Institute for Nuclear Science and Technology, Hanoi. 2009; 181.
- Loan DT, Tan NH, Khoa DT, Margueron J. Equa- tion of State of Neutron Star Matter and the Nuclear Symmetry Energy. Physical Review C. 2011; 83(6): 065809.
- Tan NH, Loan DT, Khoa DT, Margueron J. Mean Field Study of Hot β-Stable Protoneutron Star Matter: Impact of the Symmetry Energy and Nucleon Effective Mass. Physical Review C. 2016; 93(3): 035806.
- Khoa DT, Oertzen VW. Refractive Alpha-Nucleus Scat- tering; A Probe for the Incompressibility of Cold Nuclear Matter. Physics Letters B. 1995; 342: 6-12.
- Khoa DT, Phuc NH, Loan DT, Loc BM. Nuclear Mean Field and Double-Folding Model of the Nucleus-Nucleus Optical Potential. Physical Review C. 2016; 94: 034612.
- Chien LH, Khoa DT, Cuong DC, Phuc NH. Con- sistent Mean-Field Description of the 12C+12C Optical Potential at Low Energies and the Astrophysical S-Factor. Physical Review C. 2018; 98: 064001.
- Anh NL, Phuc NH, Khoa DT, Chien LH, Phuc NTT. Folding Model Approach to the Elastic p +12,13 C Scatter- ing at Low Energies and Radiative Capture 12,13C(p, γ) Reactions. Nuclear Physics A. 2021; 1006: 122078.
- Vidana I, Providencia C, Polls A. Effect of Tensor Cor- relations on the Density Dependence of the Nuclear Symmetry Energy. Symmetry. 2015; 7:15-31.
- Loan DT, Bui ML, Dao TK. Extended Hartree-Fock Study of the Single-Particle Potential: the Nuclear Symmetry Energy, Nucleon Effective Mass and Folding Model of the Nucleon Optical Po- tential. Physical Review C. 2015l; 80: 011305(R).
- Tan NH, Khoa DT, Loan DT. Spin-Polarized β-Stable Neutron Star Matter: The Nuclear Symmetry Energy and GW170817 Constraint. Physical Review C. 2020; 102(3): 045809.
- Vidana I, Providencia C, Polls A, Rios A. Density De- pendence of the Nuclear Symmetry Energy: A Microscopic Perspective. Physical Review C. 2009; 80(4): 1-27.
- Shetty DV, Yennello SJ, Souliotis GA. Density Depen- dence of the Symmetry Energy and the Equation of State of Asymmetric Nuclear Matter. Physical Review C. 2007; 75(3): 89-92.
- Heiselberg H, Hjorth-Jensen M. Phases of Dense Matter in Neutron Stars. Physics Reports. 2000; 328(5-6): 237-327.
- Li BA, Chen LW, Fattoyev FJ, Newton WG, Xu C. Probing Nuclear Symmetry Energy and its Imprints on Properties of Nu- clei, Nuclear Reactions, Neutron Stars and Gravitational Waves. Journal of Physics: Conference Series. 2013; 413(3): 1-9.
- Khoa DT, Than SH. Isospin Dependence of 6He + p Op- tical Potential and the Symmetry Energy. Physical Review C. 2005; 71: 044601.
- Shetty DV, Yennello SJ, Botvina AS, Souliotis GA, Jandel M, Bell E, Keksis A, Soisson S, Stein B, Iglio J. Symmetry Energy and the Isospin Dependent Equation of State. Physical Review C. 2004; 70: 011601.
- Shetty DV, Yennello SJ, Souliotis GA. Density dependence of the symmetry energy and the equation of state of isospin asymmetric nuclear matter. Physical Review C. 2007; 75: 034602.
- Famiano MA, Liu T, Lynch WG, Mocko M, Rogers AM, Tsang MB, Wallace MS, Charity RJ, Komarov S, Sarantites DG, Sobotka LG, Verde G. Neutron and proton transverse emission ratio measurements and the density dependence of the asymmetry term of the nuclear equation of state. Phys Rev Lett. 2006 Aug 4;97(5):052701. doi: 10.1103/PhysRevLett.97.052701. Epub 2006 Aug 4. PMID: 17026096.
- Akmal A, Pandharipande VR, Ravenhall DG. Equation of State of Nucleon Matter and Neutron Star Structure. Physical Review C. 1998; 58:1804.
- Ochala I, Fiase JO, Gbaorun F, Bamikole JA. A Study of Asymmetric Nuclear Matter with the B3Y-Fetal Effective Interaction. International Research Journal of Pure and Applied Physics. 2021; 8 (2): 10-35.
- Basu DN, Chowdhury PR, Samanta C. Equation of State for Isospin Asymmetric Nuclear Matter Using Lane Potential. Acta Physica Polonica B. 2006; 37(10):2869-2887.