Spin ½ model in statistical mechanics and relation to a truncation of the Riemann ξ function in the Riemann Hypothesis

In the search for a solution to the Riemann Hypothesis, we have studied an approach that connects the Riemann Problem with physical modeling that refers to statistical mechanics.

Thus, we study the relation between a truncation of the Riemann ξ function in the variable z = 1-1/s, where s is the usual complex variable (s=Re(s)+i·Im(s) = ρ + i·t) and the partition function of a ferromagnetic spin 1/2 model on a circle C with long-range interaction, to give a concrete look at a strategy for a possible proof of the Riemann Hypothesis.

In mathematics, the Riemann hypothesis is a conjecture defined by Bernhard Riemann (1826-1866) in 1859. This conjecture refers to the Riemann zeta function that has its zeros only at the negative even integers and complex numbers with real part ½. In particular, Riemann affirms: “…it is very probable that all roots are real. Of course, one would wish for a rigorous proof here; I have for the time being, after some fleeting vain attempts, provisionally put aside the search for this, as it appears dispensable for the immediate objective of my investigation.” [1].

For the spin 1/2 model of Statistical Mechanics, we use an important Theorem of the last century (Theorem of Lee and Yang) concerning the locus (unit circle) of the zeros in z =exp(-2·β·H) where H is the external magnetic field (β=1/(k·T), with T the absolute temperature.

For the Riemann ξ function, we use a truncation of the series in the variable z, z=1-1/s where s = ρ+i·t.

From the relation between the two “partition functions” we obtain already for small systems (2·N, i.e. number of spin variables equal to the degree of truncation of the series of the ξ function) very satisfactory positive values of the low Li-Keiper coefficients, values above our general lower bound given in terms of the Koebe function (the Riemann Wave Background, see reference section) and below the corresponding true values of the truncated partition function of ξ in the thermodynamic limit 2·N → ∞. We notice that considering the very definition of the Li-Keiper coefficients λ_n given in terms of the log of the ξ function with the series in z by:

log(ξ(z))= ∑ ((λ_n/n)·zⁿ) = ∑(φ_n·zⁿ)

We obtained an infinite set of Equations for the partial partition functions φ_n, i.e. the cluster functions, which possess a linear lower bound - Linear bound - which gives lower bounds to the λ_n using the spin-lattice models, i.e. the Riemann wave background. The background may be summarized as follows: starting with the established lower bound for the cluster function φ_n, we obtain a function containing as an argument the Koebe function i.e. K(z)=z/(1-z)² which is given by f(z)=log(1+λ₁·K(z)) and related to the partition function of the smallest spin system, (i.e. that consisting of just two interacting spins in a magnetic field H in z= exp(-2·β·H)). In fact, the numerator of the argument of f(-z), i.e. 1+z²+(2-λ₁)·z, using the first equation for the relation of the two truncations given by 2·N·X^(2·N-1) = 2·N - λ₁, for 2·N=2 gives (2- λ₁)=X = exp(-2·β·J) and Z₂=1+z²+2·z·X (J is the two-body interaction) [2].

The expansion of the above logarithm is then given by:

$\begin{array}{l}f\left(z\right)=log\left(1+\frac{{\lambda }_{1 }.z}{{(1-z)}^2}\right)==\frac{{\lambda }_{1 }.z^1}{1}+\frac{(4.{\lambda }_{1 }-{\lambda }_1^2).z^2}{2}+\frac{(9.{\lambda }_{1 }-6.{\lambda }_1^2+{\lambda }_1^3).z^3}{3}+\\ \frac{(16.{\lambda }_{1 }-20.{\lambda }_1^2+8.{\lambda }_1^3-{\lambda }_1^4).z^4}{4}+\dots =={\displaystyle \sum }_{n=1}^{\infty }\frac{{\lambda }_n^{\text{'}}.z^n}{n}\end{array}$

Where λ_n' is our emerging positive lower bound to the Li-Keiper coefficients λ_n, given by the inequality:

λ_n ≥ λ_n' = 4·sin²(θ·n/2) with n=1, 2, ....

Notice, θ is the solution of the equation: 4·sin²(θ/2) = λ₁, i.e. θ = 0.15211929... where λ₁ is the first Li-Keiper coefficient - independent of the truth of the Riemann Hypothesis - and exactly given using the two constants (π and the Euler constant γ = 0.57..) by λ₁= 1+ γ/2 – (½)·log(4·π)=0.0230957...

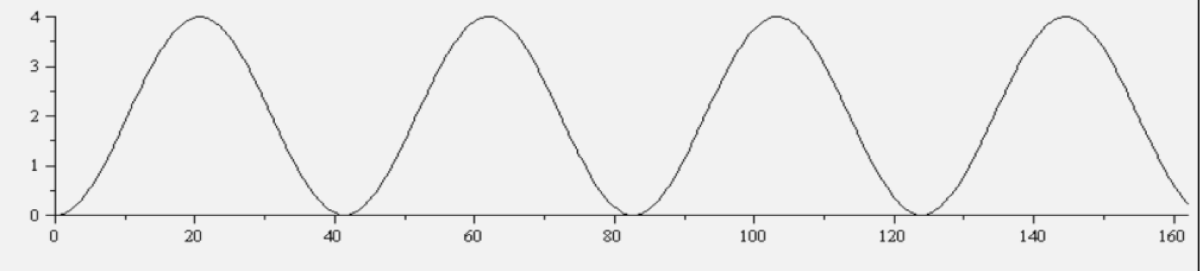
In this work, we have applied a thermodynamic modeling, to provide a possible proof of the Riemann Hypothesis. During these studies, we found a (positive) periodic function named “Riemann wave background” [3]. It depends only on γ (the Euler-Mascheroni constant) and π. Figure 1 shows the Riemann wave background. Our (positive) periodic function (Riemann wave background) depends only on γ (the Euler-Mascheroni constant) and π); i.e. on the first Li-Keiper coefficient λ₁.

λ_n' is our emerging positive lower bound to the Li-Keiper coefficients. It represents the infinite set of discrete values (n integer) in the continuous Riemann wave background, the function for n real, periodic of period about equal to 41 (Figure 1).

Other strategies for a possible proof of the Riemann Hypothesis are of course possible. We limit here to give a few important and general References, one [4] concerning the foundations of Statistical Mechanics, and the second [5,6] presents the main known equivalents to Riemann Hypothesis using analytic and computational methods. The third reports the most important approaches in the study of the Riemann Hypothesis [7] and the fourth discusses a not plausible route to proving Riemann Hypothesis [8]. References to our recent works in the above direction are also cited [2,3,9,10].

1. Riemann B. On the number of prime numbers below a given size. Monthly reports of the Berlin Academy. In Collected Works, Teubner, Leipzig (1892), Reprinted by Dover, New York (1953). Original manuscript (with English translation). Reprinted in (Borwein et al., 2008) and (Edwards, 1974). 1859.
2. Merlini D, Rusconi L. Small Ferromagnetic Systems and Polynomial Truncations of the Riemann Function ξ. Chaos and Complexity Letters. 2018; 12(2): 101-122.
3. Merlini D, Sala M, Sala N. Riemann wave background. 2019. https://www.researchgate.net/publication/335867792_Riemann_wave_background.
4. Baxter RJ. Exactly Solved Models in Statistical Mechanics. Academic Press. 1974.
5. Broughan K. Equivalents of the Riemann Hypothesis: Volume One: Arithmetic Equivalents. Cambridge University Press. 2017.
6. Broughan K. Equivalents of the Riemann Hypothesis: Volume Two: Analytic Equivalents. Cambridge University Press. 2017.
7. Conrey B. Riemann’s Hypothesis. American Institute of Mathematics. 2019. https://aimath.org/~kaur/publications/90.pdf
8. Farmer DW. Jensen polynomials are not a plausible route to proving the Riemann Hypothesis. Advances in Mathematics. 2020; 411:108781.
9. Merlini D, Rusconi L, Sala M, Sala N. Blocks partition analysis: a possible positivity of the Li-Keiper coefficients. Chaos and Complexity Letters. 2022; 16(2): 95-105.
10. Merlini D, Sala M, Sala N. Primitive Riemann Wave at Re(s) = 0.9 and Application. Chaos and Complexity Letters. 2020; 14(1): 3-32.