Unsteady and Incompressible Magneto-Hydrodynamics Blood Flow in an Inclined Cylindrical Channel

In the current study, the blood flow through an inclined cylindrical tube subjected to an external magnetic field is evaluated. The blood flow has been considered under the consequence of a transverse magnetic field. Previously the mathematical model was solved by using Caputo-Fabrizio (CF) fractional order derivative with a non-singular kernel which has the limitations like it fails to satisfy the fundamental theorem of fractional calculus. Whereas, in the present study Adomian Decomposition Method (ADM) which is suitable for all types of linear and non-linear differential equations is used. The flow of magnetized blood in an inclined cylindrical tube has been studied by using the ADM. An external magnetic field and an oscillating pressure gradient drove the blood flow. ADM algorithm has been developed and used to find the Adomian solution. Computer software MATHEMATICA has been used to visualize the influence of various flow characteristics such as Hartmann number (Ha), different radial locations and angle of inclination on the Adomian velocity. Due to the Lorentz effect and central radial location, the results show that the magnetic field diminishes the velocities of blood. Meanwhile, progressive inclination angle enhanced the blood flow.

The term "magnetohydrodynamics" (MHD) is formed from the words “magneto” (magnetism) “hydro” (water), and “dynamics” (mobility). Hannes Alfven pioneered the field of MHD [1], for which he received the Nobel Prize in Physics. The MHD nanoliquid flow is evaluated by taking it with the magnetic and aluminum oxide nanoparticles. The variable wall temperature was considered. The velocity of the ferro-fluid is strongly dependent on the viscosity and thermal conductivity along with the Lorentz’s forces. Fluids that are impacted by magnetic fields are known as magnetic fluids. Blood is the most common biomagnetic fluid that may be handled as a magnetic fluid since erythrocytes contain hemoglobin particles, which are iron oxides that are only found in adult blood. Furthermore, the condition of oxygenation has an impact on its magnetic property [2,3]. Blood is a viscous crimson liquid that circulates via blood arteries. It is one of the fundamental components that make up the human body and has a powerful nourishing influence on it. Blood is a mixture of white, red and platelets cells suspended in consistent solution known as plasma. Plasma includes 7% of the major proteins and 90% water [4].

The fluid flow through an inclined cylinder has tremendous applications in industry and engineering. This type phenomena are very important in cooling electronic devices, in a gas turbine during cooling the wall of combustion chamber, flows in the atmosphere and oceans, automobile demister, during an emergency shutdown of atomic reactor, boilers, defroster system, in the system of solar energy and in a low velocity situation heat exchangers set [5]. It is clear that in biological mechanisms, not all capillaries are horizontal, and only a few are slanted. The blood artery is represented as an inclined cylindrical tube exposed to an external magnetism in the current study, which was inspired by the previous investigations. The fluctuating pressure differential in the z-direction drove blood flow.

Previously the blood flow model was solved in the presence of magnetic particles by using CF fractional order derivative with non-singular kernel which has limitation like it fails to satisfy the fundamental theorem of fractional calculus [6-9]. Since they not do allow the reality of a corresponding convolution integral of which the derivative is the left-inverse; and the value of the derivative at the initial time t = 0 is always zero, which assess an abnormal regulation on differential equations and ideal where these derivative can be used. Where as in the present study ADM is used which is suitable for all types of differential equations [11,12] linear, non-linear homogenous or inhomogeneous. The Adomain decomposition point of view was used to manage collections of linear and non-linear problems.

The research of MHD is extremely beneficial in biotechnology, particularly in the areas of Magnetic Resonance Imaging (MRI), cancer therapy and heart attack [10]. A mathematical formalism of blood flow in a microscopic artery exposed to a magnetic intensity has earlier been explored [11]. Their outcomes showed that as the magnetic pitch grew, the flow and velocity rate decreased. The blood flow in a catheterized stenosis artery exposed to slip velocity while a transverse magnetic field was present was investigated [12]. It was discovered that when the intensity of the transverse magnetic field rose, the wall shear stress increased. Gold nanoparticles were used to study MHD blood flow [13]. In a hollow blood artery, the blood was administered as a nanofluid. The least square technique (LSM) and the RK4 method were used to tackle this issue. The velocity was observed to decrease due to the transverse action of the magnetic field. The influence of magnetic field on a blood flow inside oscillatory arteries was studied using a fractional derivative-based mathematical model [14]. Tassaddiq [15] analyzed the upshot of nanomaterials on the thermal efficiency of nanomaterials using heat flow model (micropolar fluid). Vaidya, et al. [16] inspected the effects of various features on Bingham fluid in MHD peristaltic transmission. Dynamical forces acting on the conducting fluid cause the fluid stream to shift. Since this idea focuses on medicine transfer and blood flow management during procedures, the impact of MHD flow with radiative and permeable boundary conditions is addressed. Alghamdi, et al. [17] used blood as a transportation fluid to study the laminar flow of silver and aluminum oxide hybrid nanoliquids within two impermeable channels. In this study, the medicine administration strategy, as well as the microcirculatory system’s flow dynamic mechanism, may be altered. Under convective conditions, Nisar, et al. [18] investigated how wall suppleness changes MHD peristaltic flow through nanoliquid.

Blood is a liquid-like fluid that circulates all across the human body and that of animals. Because the fluid in this study is presumed the cleanest blood flow under the magnetic force through an inclined cylinder, it is noticed that the blood thickness is not static according to medicinal perceptions and that it can regulate the body compression, hemoglobin percentage, temperature, and vessel/artery dimension. As a result, we may consider blood to be a Newtonian fluid. In order to explore the various bloodstream configuration, a numerical approach based on Newtonian blood flow conditions and stable state was devised [19]. It was discovered that different functionalities could influence hemodynamic factors. The gold-blood principle was initiated over a longitudinal upper side of a parabolic [20]. Cuo blood transportation was studied theoretically through a stenosis artery with specific hemodynamic properties [21]. For biomedical sciences, a numerical estimate of blood in human blood vessels was replicated using Newtonian techniques with heat instability [22]. The flow of nanoliquids over an irregular channel was compared [23]. The erythrocyte cell is a significant magnetic component that has the potential to influence blood flow via arteries. By supposing magnetic influence on blood flow, a theoretical conclusion was obtained [24]. Conducting fluids are mostly employed for cellular partition, MRI or just as a conflicted agent, active substantial measurement, therapy of tumor infected cells, MHD micro pump and in the biomedical area [25]. Rana, et al. [26] took Williamson’s fluid blood and has studied the expanding and shrinking surface. Khan, et al. [27] used entropy to analyze the brain and its abnormalities, whereas gold used nanoparticles to cure cancer. Following up on the nature of blood’s thermo physical property and the use of gold nanoparticles on curved shrinking/stretched surfaces.

Some arteries in the general biological system are not precisely level or vertical. As a result, while calculating flow in sloping arteries, the impact of gravity should be taken into account. An angled, catheterized, and overlapping stenosis was studied for its unstable non-Newtonian blood flow [28]. The blood was represented as an incompressible conducting fluid moving in an asymmetric inclined channel. To tackle the problem, the authors employed the analytical perturbation approach. According to findings, as the inclination angle grows, the pressure gradient enhance. Jamil, et al. [29] explored a non-Newtonian conducting bloodstream in an inclined stenotic artery using the CF fractional derivative without a singular kernel. The impact of a diagonal magnetic pitch on unstable blood flow via an inclined porous media with the pulsatile pressure gradient was explored by Shah, et al. [30].

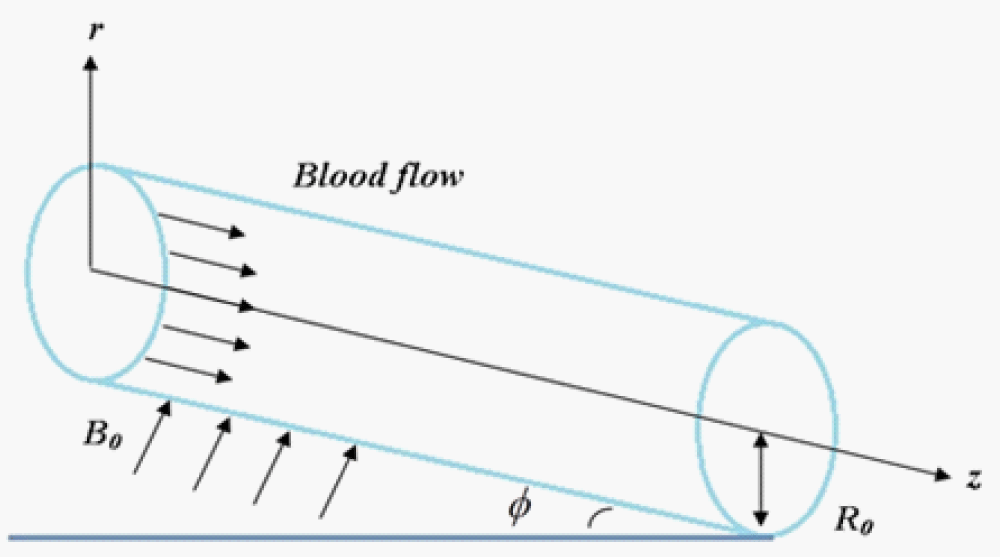
As depicted in Figure 1, blood flow is in a cylindrical tube. A homogeneous magnetic field is employed orthogonal to the flow direction while blood flows in an axial direction. At t = 0, the blood motion begins at rest, and the no-slip condition at the tube’s wall is applied, resulting in the blood having zero velocity at the tube’s wall. The Navier-stokes equations, which describe blood flow, and Maxwell’s relations, which describe the magnetic field, are the governing equations.

The problem entails solving mutually the momentum equations for fluid flow and Maxwell’s for the magnetic field connections.

By Ohm′s law, the current density $\overrightarrow{j}$ is stated by

$\overrightarrow{j}=\sigma (\overrightarrow{E}+\overrightarrow{V}\times \overrightarrow{B}),$ (1)

Where $\overrightarrow{E}$ , σ, $\overrightarrow{B}$ and $\overrightarrow{V}$ are the electrical conductivity, electric field intensity, magnetic flux intensity and velocity vector. Maxwell′s equations are:

$\nabla .\overrightarrow{B}=0,\nabla \times \overrightarrow{B}={\mu }_0\overrightarrow{j},\nabla \times \overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t},$ (2)

Where µ₀ is the magnetic permeability and ${\overrightarrow{F}}_m$ is the electromagnetic force characterized as

${\overrightarrow{F}}_m=\overrightarrow{j}\times \overrightarrow{B}=\sigma (\overrightarrow{E}+\overrightarrow{V}\times \overrightarrow{B})\times \overrightarrow{B}=-\sigma B_0^{2}u,$ (3)

The pulsatile flow in a cylindrical tube of blood with radius ‘r’ is thought under the effect of the uniform diagonal magnetic field. The modeled momentum equation can be rebound as:

$\frac{\partial u}{\partial t}=-\frac{1}{\rho }\frac{\partial p}{\partial z}+v\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}\right)-\frac{\sigma B_0^{2}sin\theta }{2}u+g\sin \varphi .$ (4)

Here ρ is the fluid density, p is the pressure, u is the fluid velocity.

$-\frac{\partial p}{\partial z}=A{}_0+A_1\cos wt,$ (5)

Where A₀ and A₁ present the constant amplitude and pressure gradient, giving rise to diastolic and systolic pressure.

We present the subsequent dimensionless parameters and variables:

$r^{\ast }=\frac{r}{a},u^{\ast }=\frac{ua}{v},v^{\ast }=\frac{va}{v},t^{\ast }=\frac{tv}{a^2},p^{\ast }\frac{p{a}^2}{p{v}^2}.$ (6)

Where $Ha=Ba\sqrt{\frac{\sigma }{\mu }}$ (Hartmann number).

Using the above parameters and dimensionless, Eqs. (4), can be inscribed as

$\frac{\partial u}{\partial t}=(A{}_0+A_1\cos wt)+v\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{1}{r}\frac{\partial u}{\partial r}\right)-H{a}^2\mu +\frac{\sin \varphi }{F}.$ (7)

The initial condition is:

$u(r,0)=1+e^r.$ (8)

ADM operator form of eq. (7) can be written as, (9)

Let us assume that, then we can write eq. (9), as (10)

eq. (10) can further be simplified by taking,

$L_{t}u=a_1+A_1\cos wt+L_{r}u+a_{2}u,$ (11)

Where $L_t=\frac{\partial }{\partial t}$ and. $L_r=\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}$ (12)

Appling $L_t{}^{-1}$ on both sides of eq. (11), and using the initial condition stated in eq. (8), where $L_t{}^{-1}={\displaystyle \underset{0}{\overset{t}{\int }}(•)dt,}$ we get:

$u(r,t)=1+e^r+a_{1}t+A_1\frac{\sin wt}{w}+L_t{}^{-1}{L}_{r}u+a_2{L}_t{}^{-1}u.$ (13)

$\begin{array}{l}{u}_0=1+e^r\\ u_1=A_1\frac{\sin wt}{w}+L_t{}^{-1}{L}_r{u}_0+a_{1}t+a_2{L}_t{}^{-1}{u}_0\\ u_{n+1}=L_t{}^{-1}{L}_r{u}_n+a_2{L}_t{}^{-1}{u}_n.\end{array}$ (14)

First finding u₁ from eq. (14)

$u_1=a_{1}t+A_1\frac{\sin wt}{w}+{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r^{}}\right)}(1+e^r)dt+a_2{\displaystyle \underset{0}{\overset{t}{\int }}(1+e^r)dt},$ (15)

$u_1=a_{1}t+A_1\frac{\sin wt}{w}+{\displaystyle \underset{0}{\overset{t}{\int }}(e^r+\frac{1}{r}{e}^r)dt}+a_2{\displaystyle \underset{0}{\overset{t}{\int }}(1+e^r)dt},$ (16)

$u_1=a_{1}t+A_1\frac{\sin wt}{w}+e^r(1+\frac{1}{r})t+a_2(1+e^r)t.$ (17)

Now finding u₂ by putting n = 1 in eq. (14), we get

$u_2=L_t{}^{-1}{L}_r{u}_1+a_2{L}_t{}^{-1}{u}_1,$ (18)

And using u₁ from eq. (17), we have

$u_2=L_t{}^{-1}{L}_r\left(\begin{array}{l}{a}_{1}t+A_1\frac{\sin wt}{w}+\frac{e^r(1+r)t}{r}\\ +(1+e^r)t\end{array}\right)+a_2{L}_t^{-1}\left(\begin{array}{l}{a}_{1}t+A_1\frac{\sin wt}{w}+\frac{e^r(1+r)t}{r}\\ +(1+e^r)t\end{array}\right),$ (19)

$u_2=\frac{1}{2}{e}^r{t}^2+\frac{e^r{t}^2}{r}+\frac{a_2{e}^r(1+r^{-1})t^2}{2}+\frac{a_1{a}_2{t}^2}{2}-\frac{A_1{a}_2\cos wt}{w^2}+\frac{e^r(1+r)t^2}{2r}+\frac{a_2(1+e^r)t^2}{2}.$ (20)

Now finding u₃ by putting n = 2 in eq. (14), and using u₂ from eq. (20), we have

$u_3=L_t{}^{-1}{L}_r{u}_2+a_2{L}_t{}^{-1}{u}_2,$ (21)

$\begin{array}{l}{u}_3=\frac{1}{3}{e}^r{t}^3+\frac{e^r{r}^{-1}{t}^3}{3}-e^r{r}^{-2}{t}^3+e^r{r}^{-3}{t}^3+\frac{a_2{e}^r{t}^3}{3}+\frac{a_2{e}^r{r}^{-2}{t}^3}{6}-\frac{a_2{e}^r{r}^{-2}{t}^3}{3}+\frac{a_2{e}^r{r}^{-3}{t}^3}{3}\\ -\frac{a_2{e}^r{t}^3}{6}-\frac{a_2{e}^r{t}^3}{3r}-\frac{a_{{}_2}^2{e}^r(1+r^{-1})t^3}{6}+\frac{a_1{a}_{{}_2}^2{t}^3}{6}-\frac{A_1{a}_2\cos wt}{w^3}+\frac{a_2{e}^r(r+1)t^3}{6r}+\frac{a_{{}_2}^2(1+e^r)t^3}{6}.\end{array}$ (22)

Finally combining all the previous results obtained in eq. (14), (7), (10) and (22), we have,

$u={\displaystyle \sum _{n=0}^3{u}_n=u_0+u_1+u_2+u_3,}$ (23)

$\begin{array}{l}u={\displaystyle \sum _{n=0}^3{u}_n=a_{1}t+A_1\frac{\sin wt}{w}+e^r(\frac{r+1}{r})t+a_2(1+e^r)t+\frac{1}{2}{e}^r{t}^2}+\frac{e^r{t}^2}{r}+\frac{a_2{e}^r(1+r^{-1})t^2}{2}\\ +\frac{a_1{a}_2{t}^2}{2}-\frac{A_1{a}_2\cos wt}{w^2}+\frac{e^r(r+1)t^2}{2r}+\frac{a_2(1+e^r)t^2}{2}+\frac{1}{3}{e}^r{t}^3+\frac{e^r{r}^{-1}{t}^3}{3}-e^r{r}^{-2}{t}^3+e^r{r}^{-3}{t}^3\\ +\frac{a_2{e}^r{t}^2}{3}+\frac{a_2{e}^r{r}^{-2}{t}^3}{6}-\frac{a_2{e}^r{r}^{-2}{t}^3}{3}+\frac{a_2{e}^r{r}^{-3}{t}^3}{3}-\frac{a_2{e}^r{t}^3}{6}-\frac{a_2{e}^r{t}^3}{3r}-\frac{a_2^2{e}^r(1+r^{-1})t^3}{6}+\frac{a_1{a}_2^2{t}^3}{6}\\ -\frac{A_1{a}_2\cos wt}{w^3}+\frac{a_2{e}^r(r+1)t^3}{6r}+\frac{a_{{}_2}^2{e}^r(1+e^r)t^3}{6}.\end{array}$ (24)

Skin friction coefficient

Skin friction is friction of blood that is against the artery membrane.

$-\frac{\partial p}{\partial z}= \frac{1}{r}\frac{\partial \left(rr\right)}{\partial r} ,$ (25)

$\tau is finite at r=0.$ (26)

Integrating (25) and using (26), we obtain

$\tau = -\frac{r}{2}\frac{\partial p}{\partial z} .$ (27)

Since, in our study we are considering external pressure gradient as given, so one of possible solution of the skin friction is,

$-\frac{\partial p}{\partial z}= A_{O }+A_1\cos wt$ (28)

$\tau = \frac{r}{2} (A_{O }+A_1\cos wt)$ (29)

In this segment, the properties of different constraints on Adomian based solutions of unsteady and incompressible magneto-hydrodynamics blood flow in an inclined cylindrical channel are inspected, discussed and graphically explained. Whereas, in Figures 2-4, graphs of physical flow parameters of interest contains different radial axis (0.2≤r≤0.5), rexternal magnetic field (0.2≤Ha≤0.5) and inclination angle ( $\varphi = \raisebox{1ex}{$pi$}\!\left/ \!\raisebox{-1ex}{$6$}\right.,\raisebox{1ex}{$pi$}\!\left/ \!\raisebox{-1ex}{$5$}\right.,\raisebox{1ex}{$pi$}\!\left/ \!\raisebox{-1ex}{$4$}\right.,\raisebox{1ex}{$pi$}\!\left/ \!\raisebox{-1ex}{$3$}\right.$ ). In our model we only impose initial condition on the governing equation and there is no condition on the boundary due to which all the curves are not converging to the single point, where the boundary condition is used, due to which all the plots are converging. Other fluid flow constants are A0=0.5, A1=0.6, R=0.5, w = $\raisebox{1ex}{$pi$}\!\left/ \!\raisebox{-1ex}{$4$}\right.$ .

ADM solution versus different flow parameters are plotted in the Figures 2-4. Moreover, to explain the effect of radial axis r, external magnetic field Ha and inclination angle φ, velocity profile u(r, t) is designed against the time variable t.

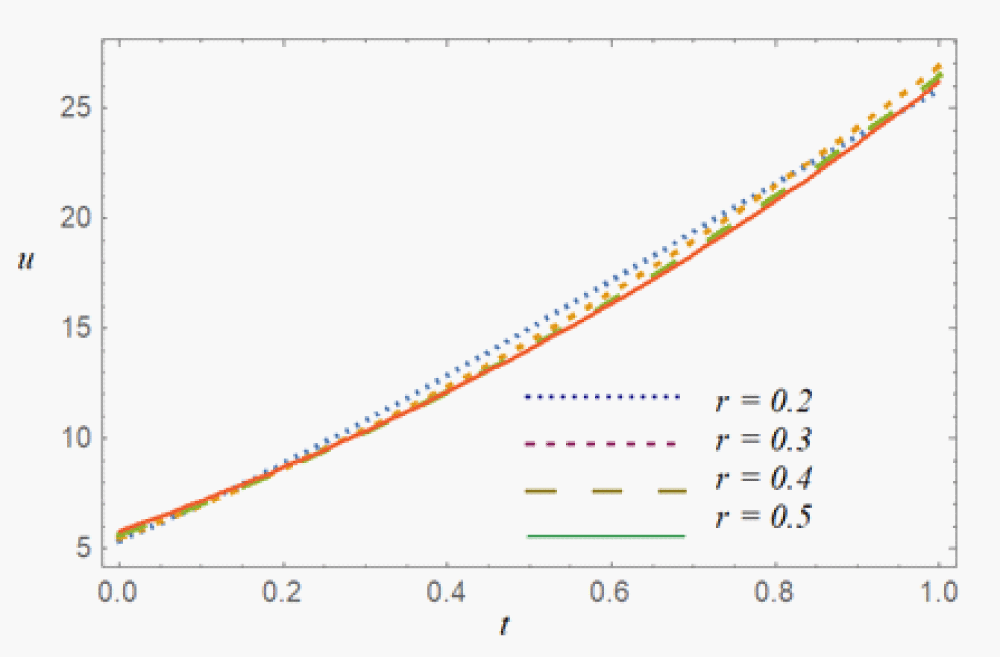
Figure 2 is showing blood velocity at different radial r components against t. Cylindrical channel flow at different radial positions is inspected. Initially for t ≤ 0.2 blood flow velocity is almost same at all the radial locations but for t > 0.2, it is maximum at the boundary then as compared to the central location.

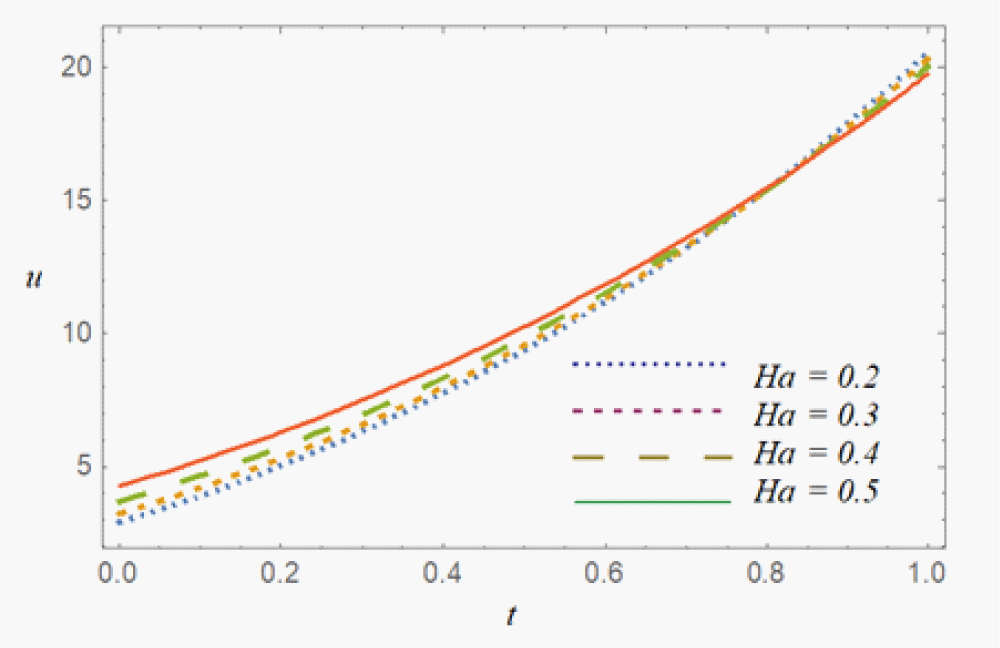
In Figure 3 external magnetic field effect on the blood flow is investigated. Enhanced flow behavior was recorded, due to reduction of blood viscosity. But later own due to the gradual enhancement of Lorentz force the normal blood flow velocity become decreases. We can conclude that by applying the sufficient amount of external magnetic field we can control the blood flow. This finding might be beneficial in some medical treatment practices.

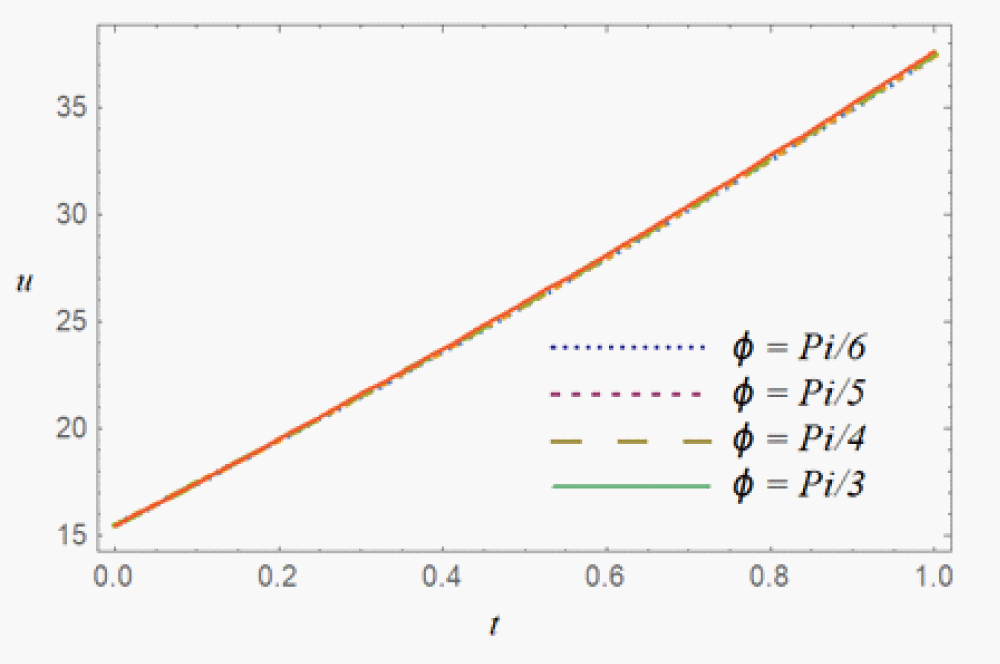
The velocity profile u(r, t) at different inclination angles φ are plotted in Figure 4. It was noted that the fluid is faster with the arterial inclination, as compared to the non-inclined artery.

The blood flow through an inclined cylinder has been exposed to a transverse magnetic field has been studied using a mathematical model. Previously the mathematical model was solved in the presence of magnetic particles by using Caputo-fabrizio (CF) fractional order derivative with non-singular kernel. The semi analytical ADM technique was used to solve the controlling non-dimensional PDEs and to create a velocity profile for blood flow. Initially, the velocity of blood increases due to reduced viscosity but later own decreases due to Lorentz force with Hartmann number. Nonetheless, when the inclination angle increases, the velocity increases. The numerical findings reveal that the inclination angle affects the flow velocity inside the cylindrical artery significantly. This discovery might aid in the identification and treatment of certain medical conditions. Furthermore, the recent discovery may lead to improved pad and machine designs.

1. Bogoliubov NN, Mitropol?skij JA, Mitropol'skii IA, Mitropolsky YA, Asymptotic methods in the theory of non-linear oscillations. 1961; 0-677-20050-1, 10, CRC Press.
2. Sheikh NA, Ching DLC, Khan I. A comprehensive review on theoretical aspects of nanofluids: exact solutions and analysis. Symmetry. 2020; 12: 1-24.
3. Higashi T, Yamagishi A, Takeuchi T, Kawaguchi N, Sagawa S, Onishi S, Date M. Orientation of erythrocytes in a strong static magnetic field. Blood. 1993 Aug 15;82(4):1328-34. PMID: 8353291.
4. Srivastava N. Analysis of Flow Characteristics of the Blood Flowing through an Inclined Tapered Porous Artery with Mild Stenosis under the Influence of an Inclined Magnetic Field. J Biophys. 2014;2014:797142. doi: 10.1155/2014/797142. Epub 2014 Feb 25. PMID: 24719614; PMCID: PMC3955598.
5. Hayat T, Qayyum S, Alsaedi A, Asghar S. Radiation effects on the mixed convection flow induced by an inclined stretching cylinder with non-uniform heat source/sink. PLoS One. 2017 Apr 25;12(4):e0175584. doi: 10.1371/journal.pone.0175584. PMID: 28441392; PMCID: PMC5404794.
6. Diethelm K, Garrappa P, Giusti A, Stynes M. Why fractional derivatives with non-singular kernels should not be used. 2020; 23: 610-634.
7. Atangana A, Secer A. A Note on Fractional order Derivatives and Table of Fractional Derivatives of some special functions. 2013; 8.
8. Matlob MA, Jamali Y. The Concepts and Applications of Fractional Order Differential Calculus in Modeling of Viscoelastic Systems: A Primer. Crit Rev Biomed Eng. 2019;47(4):249-276. doi: 10.1615/CritRevBiomedEng.2018028368. PMID: 31679259.
9. Diethelm K, Garrappa R, Giusti A, Stynes M. Why Fractional Derivatives With Nonsingular Kernels Should Not Used. 2020; 23 : 610-634.
10. Dehghan M, Tatari M. The use of Adomain Decomposition Method for solving problems in calculus of variations. vol. 2006, pp. 1-12, 12-09-2005.
11. Adomian G. A Review of the Decomposition Method in applied Matthematics. 1988; 135: 501-544.
12. Das C, Wang G, Payne F. Some practical applications of magnetohydrodynamic pumping, Sensors and Actuators A: Physical. 2013; 2: 43-48.
13. R. Bali, & U. Awasthi, "Mathematical model of blood flow in small blood vessel in the presence of magnetic field" Applied Mathematics, vol. 2 no. 2 pp. 264-269, 2011.
14. Sharma MK, Singh K, Bansal S. Pulsatile MHD flow in an inclined catheterized stenosed artery with slip on the wall. Journal of Biomedical Science and Engineering. 2014; 7: 194-207.
15. Hatami M, Hatami J, Ganji DD. Computer simulation of MHD blood conveying gold nanoparticles as a third grade non-Newtonian nanofluid in a hollow porous vessel. Comput Methods Programs Biomed. 2014 Feb;113(2):632-41. doi: 10.1016/j.cmpb.2013.11.001. Epub 2013 Nov 13. PMID: 24286727.
16. Bansi CDK, Tabi CB, Motsumi TG, Mohamadou A. Fractional blood flow in oscillatory arteries with thermal radiation and magnetic field effects. Journal of Magnetism and Magnetic Materials. 2018; 456: 38-45.
17. Tassaddiq A. Impact of Cattaneo-Christov heat flux model on MHD hybrid nano-micropolar fluid flow and heat transfer with viscous and joule dissipation effects. Sci Rep. 2021 Jan 11;11(1):67. doi: 10.1038/s41598-020-77419-x. PMID: 33431877; PMCID: PMC7801391.
18. Vaidya H, Rajashekhar C, Prasad KV, Khan SU, Mebarek-Oudina F, Patil A, Nagathan P. Channel flow of MHD bingham fluid due to peristalsis with multiple chemical reactions: an application to blood flow through narrow arteries. SN Applied Sciences. 2021; 3: 1-12.
19. Alghamdi W, Alsubie A, Kumam P, Saeed A, Gul T. MHD hybrid nanofluid flow comprising the medication through a blood artery. Sci Rep. 2021 Jun 2;11(1):11621. doi: 10.1038/s41598-021-91183-6. PMID: 34079026; PMCID: PMC8172945.
20. Nisar Z, Hayat T, Alsaedi A, Ahmad B. Wall properties and convective conditions in MHD radiative peristalsis flow of Eyring-Powell nanofluid. Journal of Thermal Analysis and Calorimetry. 2021; 144: 1199-1208.
21. Politis AK, Stavropoulos GP, Christolis MN, Panagopoulos FG, Vlachos NS, Markatos NC. Numerical modeling of simulated blood flow in idealized composite arterial coronary grafts: steady state simulations. J Biomech. 2007;40(5):1125-36. doi: 10.1016/j.jbiomech.2006.05.008. Epub 2006 Jul 7. PMID: 16828103.
22. Koriko OK, Animasaun IL, Mahanthesh B, Saleem S, Sarojamma G, Sivaraj R. Heat transfer in the flow of blood?gold Carreau nanofluid induced by partial slip and buoyancy. Heat Transfer-Asian Research. 2018; 47: 806-823.
23. Ijaz S, Iqbal Z, Maraj EN, Nadeem S. Investigation of Cu-CuO/blood mediated transportation in stenosed artery with unique features for theoretical outcomes of hemodynamics. Journal of Molecular Liquids. 2018; 254: 421-432.
24. Foong LK, Shirani N, Toghraie D, Zarringhalam M, Afrand M. Numerical simulation of blood flow inside an artery under applying constant heat flux using Newtonian and non-Newtonian approaches for biomedical engineering. Comput Methods Programs Biomed. 2020 Jul;190:105375. doi: 10.1016/j.cmpb.2020.105375. Epub 2020 Jan 31. PMID: 32036202.
25. Bharathi V, Vijayaragavan R, Prakash J. Comparative analysis of Cu/blood and Cu-CuO/blood nanofluids on a peristaltic flow governed by an asymmetric channel. Heat Transfer. 2020; 49: 4923-4944.
26. Chen I, Sana S. Analysis of an intensive magnetic field on blood flow: part 2. Journal of Bioelectricity. 1985; 4: 55-62.
27. Jang J, Lee SS. Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sensors and Actuators A: Physical. 2000; 80: 84-89.
28. Rana BMJ, Arifuzzaman SM, Islam S, Reza-E-Rabbi S, Al-Mamun A, Mazumder M, Khan MS. Swimming of microbes in blood flow of nano-bioconvective Williamson fluid. Thermal Science and Engineering Progress. 2021; 25: 101018.
29. Khan U, Zaib A, Khan I, Nisar KS. Insight into the dynamics of transient blood conveying gold nanoparticles when entropy generation and Lorentz force are significant. International Communications in Heat and Mass Transfer. 2021; 127: 105415.
30. Zaman NA, Sajid M. Slip effects on unsteady non-Newtonian blood flow through an inclined catheterized overlapping stenotic artery. AIP Advances. 2016; 6: 10-13.