More Information
Submitted: January 10, 2023 | Approved: January 17, 2023 | Published: January 19, 2023
How to cite this article: Yandza MJO. The time and the growth in physics. Int J Phys Res Appl. 2023; 6: 019-026.
DOI: 10.29328/journal.ijpra.1001049
Copyright License: © 2023 Yandza MJO. This is an open access article distributed under the Creative Commons Attribution License, which peRmits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Light; Time; Growth; Matter; Antimatter
Nomenclature: M: Mass [Kg]; m: mass [Kg]; T: Temperature [K]; p: Momentum [Kg.m.s-1]; F: Force [N]; E: Energy [J]; k: Factor of mass (density); u: Speed [m.s-1]; C: Celerity [m.s-1]; λ: Wavelength; V: Volume [m3]; n: normal; Xr: physical quantity received; XP: physical quantity produced; ph: refers to photon; Y: refers to particle Y; ap: refers to antiphoton; γ: refers to acceleration; ext: exterior; t: Time [s]; h: Max-Planck constant; x: Space [m]; t/x: Space-Time
The time and the growth in physics
Marcel Julmard Ongoumaka Yandza*
Marien Ngouabi University, Department of Physics and Engineering, Republic of Congo
*Address for Correspondence: Marcel Julmard Ongoumaka Yandza, Marien Ngouabi University, Department of Physics and Engineering, Republic of Congo, Email: julmard.marjus@gmail.com
In this article, we made a research on the subject of Time and Growth. In the life, the Growth is seen as the increase of mass which operates during a certain period. In physics, it is the same. By the Growth, a physical body gets its density increased. The goal of this article is to calculate or predict the energy and force that a physical system can have at its total Growth. To study the Growth, we have defined some equations which help to evaluate the Growth internal force and energy. By the same way, we have also discovered that all physical systems in the Universe are connected by the same interaction. This interaction leads to the loss of density or mass. The Time is the consequence of its manifestation. For studying the effect of this interaction, we have calculated the density of the Universe. We found that the density of the Universe is equal to the density of a photon. In other words, the Universe is a huge photon. That means, like a photon, the Universe does not know the Time. It also means that the Universe is eternal. Its Expansion (not its growth) is due by the fact that, at the moment small systems inside to it grow, the Universe maintains its density constant like a photon. Do not confuse Growth and Expansion. The Growth is the increase of the density; and the Expansion is the increase of the volume without the change of density. The Universe does not know the Growth, it knows the Expansion. All these conclusions are detailed in the development of this article.
In the nature, humans, animals and plants are under the influence of the Time. At the same moment, everything in the nature knows the Growth from the birthday till a certain period. Though the Growth is limited, its manifestation is crucial in the life. Nowadays, many researchers have attempted to explain the meaning of the Time. As example, Albert Einstein developed the Special Relativity Theory [1] and proposed his vision of the Time nature. The thermodynamic [2] and the Newton mechanics [3] both adhere to an absolute interpretation of the Time. In this paper, we cross the line by proposing another view of the Time nature. We will explain the origin of the Time and the meaning of the Growth. They are opposite. As we know by biology, the Growth is the increase of matter; that means the increase of density. And, the Time is clearly the effect resulted by the loss of matter; because when the Growth is total, the physical body cannot grow again. It becomes old and loses its mass. It is an evidence in the nature.
In our precedent article [4], we explained that the Time is the measure of the interaction between the matter of a system and the antimatter produced. The Time is related to the loss of mass. In this previous article, we do not explain the Growth, which appears as the opposite. However, we have established some equations to define the internal force and energy. The equations that we got in this prior article are absolute. They are defined by the light view point (section 2). As application, they permit to calculate the characteristics of a photon. As result, we got the value of the mass of photon near to the experiments [5]. The problem with these equations is the fact that they are different of the equation proposing by the Einstein’s Relativity Theory [6]. The values obtained by numerical application are superior than E = m c2. To solve this problem, we have associated our equations to the Growth of the physical bodies. That means, when we have a system of mass m, we can predict its energy at its total Growth, by the equation of the internal energy that found in the precedent article [4]. Don’t worry, we will explain it again in this new article. At the same line, we have united the equations of Growth to the normal state equations (Internal energy of Relativity for example).
By exploring the Time and the Growth, we have discovered two Laws which explain the dynamic of Universe. The First Law is referring to the conservation of momentum from one system to another. And, the Second Law is about the global interaction between all physical bodies in the Universe. By global interaction, we mean that every piece of matter in the Universe is connected to another by the same force or energy. We will explain this mechanism in the section 6. And, we will also calculate the volume, the mass and the density of the Universe. The calculus shows that the Universe has the same density than a single photon. In this paper, we will detailed the conclusions of these results.
Yandza first law: absolute speed
According to the Newton’s mechanics, the Space and the Time are two different separated concepts [6,7]. That means that the physical phenomena evolve in an absolute Time with the same pace everywhere in the Universe. In 1905, Albert Einstein published an article on the Special Relativity Theory. He explained that the Space and the Time are both linked and could not be studied separately. Thus, he defined a new concept called the Space-Time [8]. However, since Galileo the Time and the Space are connected by the speed. In this article, we use the variable t/x to designate the Space-Time. The variable t refers to the Time and the variable x refers to the Space.
According to the First Newton Law, when a physical system is not under the action of any force, it moves rectilinearly and its speed remains constant. This law is crucial because we know that the force is the cause of the movement. So, how can a physical body move without any force? The explanation is found in the mass of the system. According to the General Relativity Theory, the mass is the condensation of much energy. The energy of mass is given by the equation E = mc2. Behind this mass or this energy, there is the force of mass. In this paper, we called this force, the internal force. The internal force is the force of mass in comparison to the internal energy. So, this force is the cause of movement when no force is exercising on a physical system.
We know that the photon has a constant maximum speed. We can also consider a single photon as the particle with the lowest energy or the lowest mass. So, that means when a physical system has a low mass, its speed is great; and when its mass is great, its speed is low. This evidence leads us to the Yandza First Law: If we consider two systems or more, when no force is exercising to them, the momentum (masse*speed) is conserved from one system to another [4]. The application of Yandza First Law is given by the following equations (1):
(1)
m: mass of a physical body
mph: mass of a photon
u: speed of a physical body
c: celerity (speed of the light)
The value of the speed calculated by this way represents the absolute speed. The absolute speed is the speed of a physical body by referring to the light viewpoint. By this manner, we discover that like the speed of light is always constant, its energy (or its mass) also cannot be changed (4). Certainly, its internal force is also invariant. We have concluded that not only celerity but all physical characteristics (speed, energy, mass, force) of the photon are invariants. We precise that in this article we consider a photon (particle of light) as a particle with mass [9] (we will calculate its value later).
Growth physical characteristics: internal force, energy and temperature
The Growth physical characteristics correspond to the values of internal force, energy and temperature calculated by referring to the light viewpoint. It means the value, of the force for example, determined with the absolute speed u by the equation (2). The absolute speed is found by applying the Yandza First Law (1).
Internal force: The Space-Time of the General Relativity Theory is smooth and continuous. It deforms with the presence of the matter [10]. More a physical system is heavy more the deformation of the Space-Time is great. By analogy with the internal energy, we call the internal force, the force of the mass. The measure of the internal force is proportional with the deformation of the Space-Time t/x. This evidence leads us to conclude that the force is simply an integral (deformation) of the Space-Time. By integrating the variable t/x, we find the internal force (2).
(2)
A: Integral constant
We have considered the photon as a particle with mass. So, it creates a deformation of the Space-Time. Its internal force Fph is calculated by substituting u by c in the equation (2). The expression of Fph is given by the equation (3).
(3)
Internal energy and temperature: By the same analogy with the precedent result, the internal energy is an integral of the internal force like shown in the equation (4).
(4)
The internal energy of a photon Eph is given by the equation (5).
(5)
By the same approach, we find the expression of the temperature TG. For that, we use the Fourier Law. The temperature is an integral of the energy (6).
(6)
The temperature TG calculated by the equation (6) is associated to the Growth internal energy.
Invariants of the universe: photon: Thanks to Special Relativity Theory, we consider the speed of the light constant and absolute. On this fact, by equation (1), we see that if the speed is constant the mass also is. And, if the mass is constant, also is the energy of mass (internal energy). For these reasons, we consider that all physical characteristics of the photon in its movement (speed, mass, momentum, force, energy, temperature) are constant and absolute. Thus, we will evaluate the physical characteristics of other systems by referring to the characteristics of the light.
In reality, the energy of photon is effectively constant. The wavelength λ, badly interpreted as the sign of the wave, is in reality the distance between two photons of the same radiation. That means, the light is not a wave but a complex of particles called photons.
Now, let see how we can adopt the energy of photon without considering light like a wave. If the photons are near one to another (λ is small), their energies sum. Consequently, the radiation presents a global intense energy. That is the case of the ultraviolet. And, if the photons are far one to another (λ is great), the radiation has a global weak energy. So, we conclude that the energy of the electromagnetic radiation E varies proportionally with the energy of photon Eph; and varies inversely proportional with the wavelength λ (distance between photons) like shown in the equation (7).
(7)
(8)
By equaling the Yandza’s equation (7) with the Max-Planck’s equation (8), we determine the energy of photon Eph (9).
(9)
By another view, the photon is a particle with the lowest energy in the Universe. We admit that the value of its energy Eph corresponds to λ = 1 meter in the Max-Planck’s equation (7). In the article [4], it was an error to admit that the wavelength could not exceed one meter. If the radiation has photons so far one to another (great wavelength), the global energy of the radiation could be less than the energy of the single photon. The energy of the radiation E can be defined as the quantity of the energy of photon per meter.
(10)
By equaling (9) and (10), we determine the mass of the photon mph like given by the equation (11).
(11)
The momentum of the photon pph is also invariant. Its value is given by the equation (12).
(12)
By equaling (5) and (10) we determine the value of the integral constant A like shown by the equation (13).
(13)
The equations (2), (4) and (6) become respectively (14), (16) and (17). The equation (15) is deducted of (3). The equation (18) is deducted of (6).
(14)
(15)
(16)
(17)
(18)
The Table 1 presents the physical quantities that we call the invariants of the Universe. These values are the characteristics of a photon calculated above. The volume of photon Vph is calculated in section 5.
| Table 1: Invariants of the Universe. | |||
| Speed | C [m.s-1] | C | 299792458 |
| Momentum | pph [Kg.m.s-1] | h | 6,62606957.10-34< |
| Mass | mph [Kg] | 2,21021890.10-42 | |
| Force | Fph[N] | 3hc2 | 1,78656430.10-16 |
| Energy | Eph [J] | hc | 1,98644568.10-25 |
| Temperature | Tph [K] | 1,65651739.10-34 | |
| Volume | Vph[m3] | 9ph2c5 | 3,00613084.10-23 |
Normal characteristics of physical body
In the nature, humans, animals and vegetables grow from their first days to a certain period. So, we want to study this phenomenon physically. In the precedent section, we calculated the internal energy EG. The quantity of energy EG in the equation (16) is not the same with the energy of mass EG described by Einstein’s Special Relativity Theory. We call EG the Growth internal energy. It is represented the energy that the physical body will have after completing its total Growth. We state that because the value of EG is absolute and bigger than the internal energy En = mc2. However, we can find the relations which will evaluate the normal energy and force of a physical system. We call it internal force and internal energy.
The equations (14), (16) and (17) define the characteristics of a system of mass m when it attains its total Growth. In this section, we will propose the equations which establish the normal characteristics of a physical body of mass m.
To begin, the equation (16) can be written by the following scheme:
(19)
By equaling (19) and (16), we find the relation between the internal energy and the energy of the photon (20):
(20)
By observing the equations (16) and (19), we find that by linking the Growth internal energy EG and the internal energy En in equation (19), the exponent of km is reduced by one. So, we can deduct the relation between the Growth internal force FG and the internal force Fn as shown by equation (21).
(21)
By equaling (14) and (21), we find the equation of the internal force (22).
(22)
We can also deduct the expression of the temperature Tn like we did for the internal force and energy.
(22′)
(22′′)
The difference of energy represents the energy added by Growth. The same for which represents the force added by Growth.
Shape of the universe: mass, volume and density
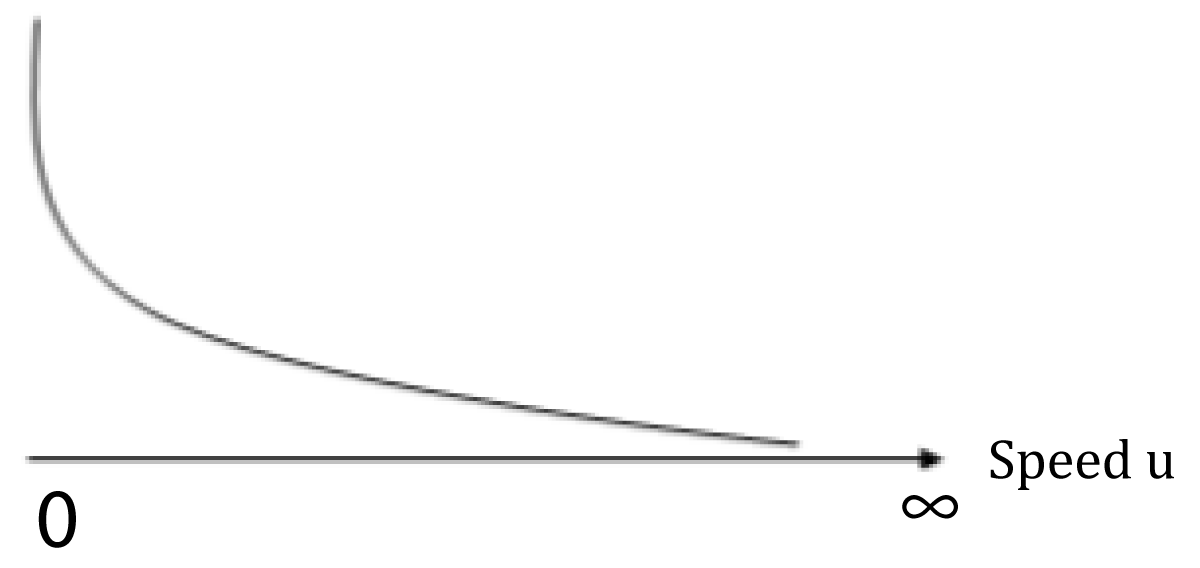
The equation (2) presents the relation between the internal force of a physical system and its absolute speed. With the Growth which operates, the mass of the system increases and its speed changes. In the Figure 1, we draw the curve of the internal force.
Figure 1: Line of internal force.
We have considered the force as the deformation of the Space-Time. By summing all these lines of force in the Universe and by applying the symmetry, we discover that the Universe has a conical shape (Figure 2).
Figure 2: Shape of the Universe.
The volume of the Universe VG is obtained by integrating the shape of the Universe like presenting by the Figure 2. The integral calculus is presented by the equation (23) and the final result by (24).
(23)
(24)
Similarly with the equations (14), (16) and (17), we deduct the volume of the photon Vph (25). Vph belongs to the invariants of the Universe. Its value is in the Table 1.
(25)
So, we can relieve the volume of a photon to the volume of the entire Universe by the factor of mass (26).
(26)
Like Growth internal energy and Growth internal force, the volume presented by the equation (26) is the volume of the Universe at its full Expansion (not the full Growth, we will see the difference between Growth and Expansion later).
By referring to the equation of the Growth internal force (21) and energy (19), we deduct the normal volume of the Universe Vu given by the equation (27).
(27)
By equaling (26) and (27), we find the normal volume of the Universe Vu (28).
(28)
By replacing we finally find the relation between the density of the Universe ρu and the density of a photon ρρh (29).
(29)
The equation (29) shows that the density of the Universe is equal to the density of a photon. In other words, the Universe is a huge photon. Like the photon escapes from the Time, the Universe also does. And, like the photon escapes from the Growth (because its characteristics are invariant), the Universe also does. So, the Universe does not know the Growth because the Growth is the change of the density by the increase of mass. The Growth of the several small systems in the Universe leads to its Expansion (increase of volume without changing the density) because the Universe conserves its density equal to the density of a photon ρρh. The volume of the Expansion is given by (26).
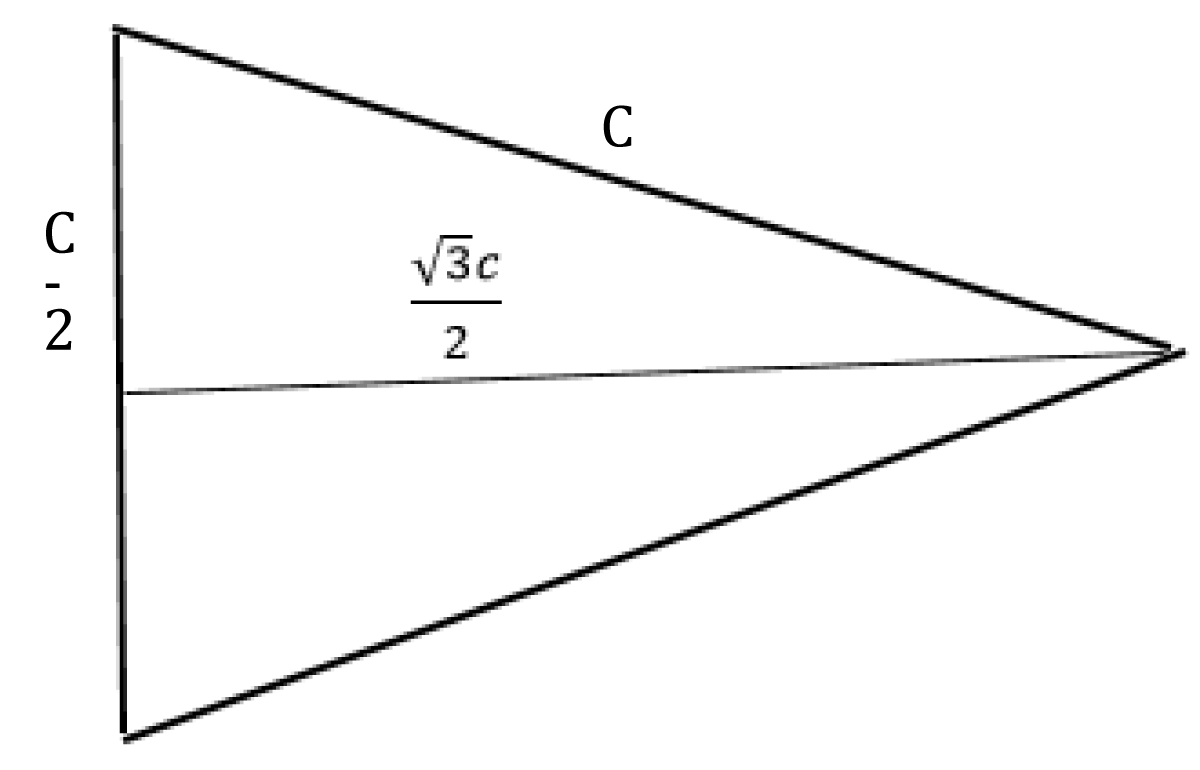
Now, we define a method to calculate the normal volume of the Universe. To begin, we know that in one unit of Time, or one second, the distance that the photon can cover is equal to c meters. That evidence is found by the following equality: . So, the conical volume that the photon can colonize in one second Vmax is given by the equation (30). The dimension of the related volume is shown by the Figure 3.
Figure 3: Volume colonized by a single photon per second.
(30)
The proportion represents the number of units obtained by filling the volume Vmax by the volume of photon Vph. That value is the maximal unit of volume. By the same rule, it is evident that the proportion is also the number of the volume Vmax that can be contained in the volume of the Universe Vu. So, the volume of the Universe Vu is calculated by the equation (31).
(31)
By replacing Vmax and Vph by their quantity, we find the normal volume of the Universe Vu (32).
(32)
The mass of the Universe is found by replacing Vu by its quantity like shown by (32) in the equation (33).
(33)
So, we find the mass of the Universe Mu like shown by the equation (33’).
(33′)
The numerical application leads us to find the following values: the volume of the Universe and the mass of the Universe Kg. The Expansion of the Universe has two causes: the first is the Growth of physical systems in the Universe. The second one is the presence of other Universes near to our Universe. When our Universe receives mass, its volume increases to maintain its density constant.
Yandza second law: loss of density and acceleration
To introduce the Yandza Second Law, we first mention what Newton states. Newton declares that any physical system in movement, under the action of an exterior force Fext, is attracted by the force of the Earth (Newton Second Law). The force of this attraction is proportional to the mass of the physical system [11] like shown by the equation (34).
(34)
Now, we consider a physical system (M) of mass m in movement. According to Newton, (M) is under controlled by the force of the Earth FT [11]. In section 2, we defined the internal force as the force of mass, responsible of the movement without any other exterior force. By the way of this definition, we see that the force with it the Earth exerts its attraction to the Moon and the other systems is simply its internal force.
Now, let see clearly the interactions between the Earth and the system (M) of mass m and internal force Fm. We consider that (M) levitates like a satellite. By studying the linear movement of the system (M) in the Space, we observe that everywhere the Earth goes, the physical system (M) is. It becomes clear that (M) is linked with the Earth. They go to the same speed. So, the evidence shows that the absolute speed of the earth is equal to the absolute speed of the system (M); because they move to the same speed (1). According to the equation (2), the equality of the speeds leads to the equality of the internal forces Fm = FT. In another view, the equation (1) specifies that the Earth and the system (M) could not have the same absolute speed because their masses are different. The only case in which the system (M) reaches the speed of the Earth is the appearance of an acceleration in its movement. With this acceleration is engaged the acceleration force Fγ. So, the balance of forces applied to the system (M) is shown by the equation (35).
(35)
FT: Internal force of the Earth (T means Terre in French)
The equation (35) is incorrect; because only the internal force of the earth FT is considered as the cause of the attraction. In reality, the source of the attraction comes also by the interactions with the other systems. First, the Earth is attracted by the Sun and develops an acceleration to reach the internal force of the Sun Fs. So does the system (M). Second, the Sun is accelerated by the galaxy (the Milky Way). That implicates a new acceleration on (M). Third, the Milky Way is also accelerated by the rest of the galaxies of the Universe. That will also increase the acceleration of the Earth which will be simultaneously applied on the system (M). The movement of the system (M) depends on the sum of these different contributions. The new balance of forces applied to the system (M) is shown by the equation (36).
(36)
Fγs: acceleration force of the Earth under the action of the Sun
Fγ∞: acceleration force of the Earth under the action of the infinity
Mu: mass of the Universe
Fu: internal force of the Universe
The action of all these contributions, we see in the equation (36), represents clearly the internal force of the Universe at the scale of the volume of the physical system (M). The equation (36) shows that, as the physical body (M) is little than the Universe, for the same volume, its internal force is equal to the internal force of the Universe. According to (22), the same force means all the two have the same mass for the same volume. So, in the Universe, wherever they are, all physical bodies are under the action of a same force. Their densities stretch to the density of the Universe which is equal to the density of a photon. And, the loss of density leads to an acceleration. This is the statement of Yandza Second Law. This analysis can be applied to any other physical systems in the Universe. In the article [4], we made an error by thinking that the sum of different contributions is equal to the force of a photon. It is only true at the scale of the volume of a photon. By replacing m by mph in (36), we find it out. In reality, for any scale, the internal force of the studied system is calculated by replacing the mass m in (36) by ρph V; because all systems stretch to the density of a photon. The final application of Yandza Second Law is given by the equation (37).
(37)
Like the density of the Universe (density of photon) is the smallest, physical bodies in the Universe stretch to lose their masses. The only way to explain this loss of mass, is to consider the appearance of antiparticle from the Space-Time. So, the force of acceleration Fγ is a negative force of antiparticle Fap. In the precedent section, we define the Growth as the natural increase of mass. To apply the Yandza Second Law, we will consider that the studied system has attained its total Growth. In reality, the two phenomena operate simultaneously. But in our research, we will study them apart. We will consider that the total Growth is attained before studied the Time. So, we replace the internal force Fm by the Growth internal force FG (38).
(38)
We note .
V: volume of the physical body.
Vph: volume of photon
By (38) we find that the Space-Time produces the anti-particles of mass equal to the mass of the photon (the smallest in the Universe). We call these antiparticles: antiphotons.
The equation (38) is not instantaneous. The decrease of the mass in the Universe operates progressively like the effect of an effervescent tablet in water. That means that the equality is verified at the end of the phenomenon. Due to the interactions between matter and antimatter, the equation (38) reveals the disintegration of the initial mass to the state of the photon [12]. To be to the state of photon means to have the same density than a photon. However, at each instant of the disintegration, an equality is verified in term of mass, momentum, force and energy. The equations (39), (40) and (41) present these equalities.
(39)
(40)
(41)
: mass of antiparticles received (if the system receives antiparticles)
: mass of antiparticles produced
Now, we consider that the precedent system (M) is made of antimatter. All the remarks we made stay applicable. But, instead of generating a flux of antiparticles (negative force ), the system (M) will receive from the Universe a flux of particles (positive force ). So, in one case (matter) we have the production of antiparticles and in another one (antimatter) we have the production of particles [13]. In the vision to unit these two kinds of production, we postulate that only one particle is emitting. We call that particle: particle Y.
The particle Y has the property to transform into an antiphoton when matter is around; and to transform also into a photon when antimatter is surrounded it. Its mass is equal to the mass of photon or antiphoton mph. By opposition to the photon, the antiphoton has a negative energy. We think that the antiparticles produced are antiphotons because the photon has the smallest energy in the Universe; and antiphotons also. If any particle must be produced, it is evident that its energy is the lowest; moreover its production is linked with the Time (section 7). Therefore we called these antiparticles, antiphotons.
The time and the growth
According to the results we found in the section 6, the Space-Time produces matter and antimatter by emitting the particles Y. However, the equations (39), (40) and (41) show that at the appearance of a particle (or an antiparticle) is engaged an accounting of Time. In fact, without the initial mass, there is no production of particles or antiparticles. Without these productions, there is no disintegration of the initial mass to the state of a photon. So, the Time is directly linked to the production of particles Y.
For a system made of matter, the Time is the measure of the interaction between matter and the total mass of the antiparticles (antiphotons) produced. For a system made of antimatter, the Time is the measure of the interaction between the antimatter and the total mass of the photons produced.
For measuring the Time t needed to disintegrate a matter to the state of a photon, it is compulsory to determine the factor of mass kΥ associated to the production of photons and antiphotons; because at the emission of one single photon (or antiphoton) is corresponding one unit of Time like shown by equations (42) and (43). We insist on the fact that the mass of the antiphotons (or photons) received does not enter in the calculus of the Time; because its effect on the physical system is instantaneous. That effect is already considered in the mass balance (39).
(42)
(43)
Like we saw in the section 6, the study of the Time (production of antiparticles) is preceded by the study of the Growth. In reality, the two phenomena operate simultaneously. But in our research, we will consider that the total Growth is attained before studying the Time. If we do not take account the Growth, the value of the Time t will be wrong. The Growth is the production of additional mass mp which increases the density. We propose the equation (44) and (45) to present the interaction of mp with the initial mass m.
(44′)
(44)
(45)
With
Mu: normal mass of the Universe
m: mass of the physical body
Fu,G: force of the Universe at its total Expansion
Eu,G: energy of the Universe at its total Expansion
Behind and there is a mass of the Growth. We note it mp. The measure of the Growth is the proportion of the mass produced mp in relation to the initial mass m (46).
(46)
De-Broglie assumed that the rest mass of photon is about 10-54 Kg [5]. Different types of experiments have been done which shows that mass of photon; by satellite measurement of Earth’s magnetic field is 4. 10-51 Kg [13], low frequency parallel resonance circuit is 10-52 Kg [14], solar wind experiments is 1,5. 10-54 Kg [15]. Using the frequency-dependent Time delays in measurements of the dispersion measures (DMs) of fast radio bursts (FRBs) on FRB 150418 and FRB 121102, the photon mass is 3,2. 10-50 Kg [16] and 3,9. 10-50 Kg [17] respectively. All these data are calculated indirectly. Experimental verification is very difficult due to very light mass of light [18]. The very recent experiments revealed the mass of the photon as 10-54 Kg [19]. That experimental value is not yet confirmed. There is not a rich bibliography on this subject. However, the value we obtained is 2,21021890.10-42 Kg. We have also confirmed that photon and antiphoton do not accelerate because their internal force is invariant in the Universe; like demonstrated in relativity [20].
The question related to the shape of the Universe is central is this research. In our bibliography, we found two types of theories which develop a certain idea on the shape of the Universe. The first one presents the Universe like a flat Space [15]. The second one attests that the Universe is a spherical shape [16]. For now, we do not totally reject the conclusions of these researches. But, we think that in these two cases, the authors did not take account the effects of the internal forces applied in the Universe. A flat Universe or a spherical one turns to conical shape when internal forces are applied. That remark is a physical evidence on the basis of Relativity Theory [17] and the interpretation of the force in this paper. To make it clear, let consider a flat shape suspending in the air. When the ball falls on it, the shape deforms. If the pressure of the ball is continuously maintained on this shape, its global shape becomes conical. That is the same if we consider a spherical one. So, the shape of the Universe is conical by the fact of the internal forces.
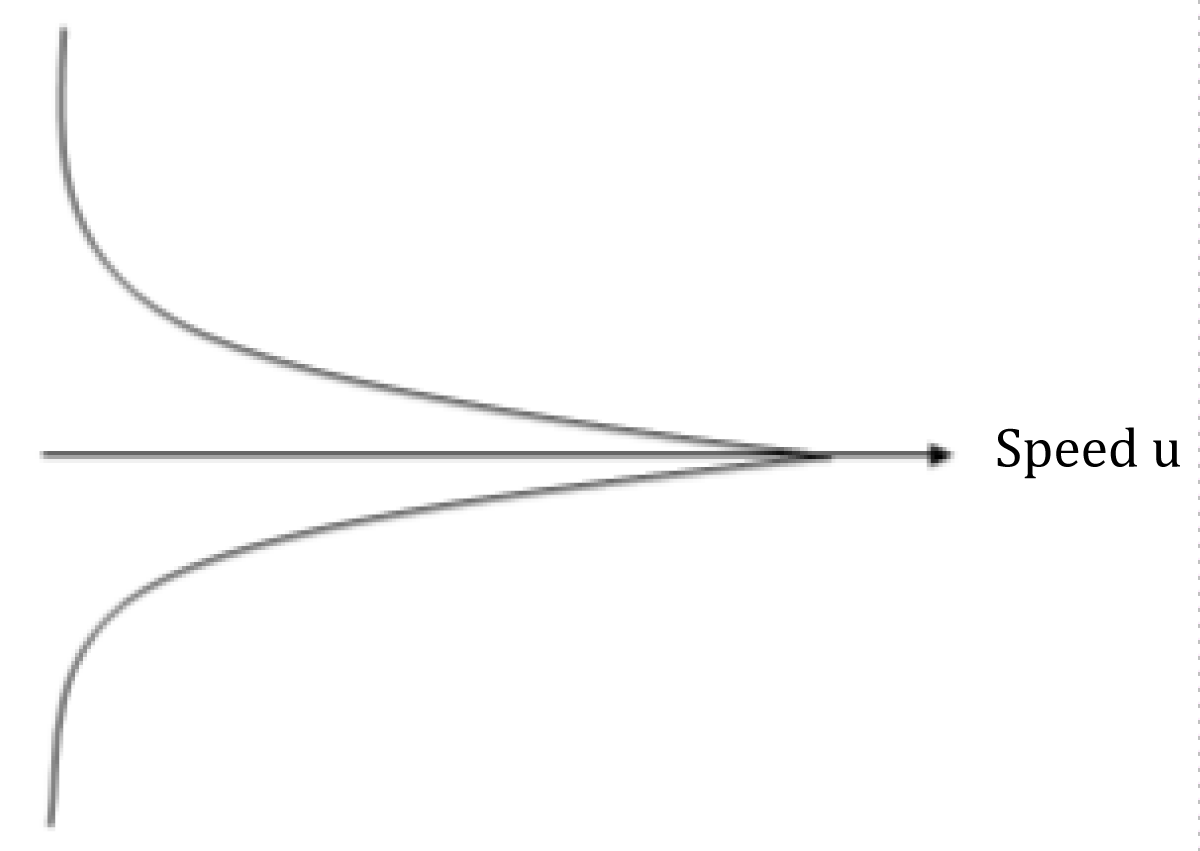
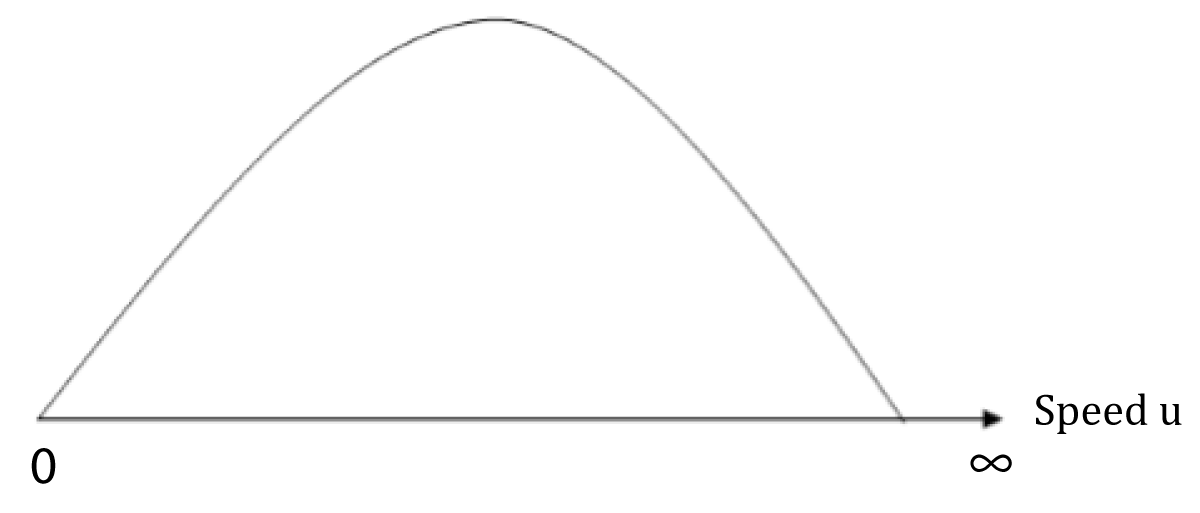
To conclude this precedent paragraph, we completely reject that the Universe is a spherical or a flat shape. First, a spherical Universe obliges the internal force having the representation of the Figure 4. It is not a correct shape because the internal force, presented in this article, continuously reduces when the speed increases by the loss of density (acceleration). But, in the case of spherical Universe, the internal force increases and then decreases after attaining its extremum. That would state that big stars like the Sun (with extreme low speed) have approximately the same internal force than the photon (with extreme high speed). That is completely incompatible. Second, in the same line, by considering a flat Universe (Figure 5), no acceleration can be operated. The internal force is always constant. That is opposed with Yandza Second Law. The fact is any system loses its density and accelerates. By the flat Universe, the internal force of the Sun for example is continuously equal to the internal force of the photon. On the basis of these arguments we effectively conclude that the Universe has a conical shape.
Figure 4: Line of internal force in a spherical Universe.
Figure 5: Line of internal force in a flat Universe.
In addition, many authors state that the Universe is an infinite system [18]. This idea is opposed to the Big Bang Theory because the infinity cannot have an origin. According to the equation (36), an infinite Universe is possible only if ku stretches to infinity (mph = o). We disagree with that option and adhere to the second community of scientists who think that the Universe is finite [19]. The finite Universe is in accordance with the Big Bang Theory and recognized that photon has a mass like we developed in this paper.
In this article, we have presented the invariants of the Universe. All, they are the characteristics of the light: its speed, its mass, its volume, its momentum, its internal force, its internal energy and its temperature. The balance of any system in the Universe depends on these invariants. We use these constants to characterize the other physical systems. By this approach, we know how to calculate the absolute speed of any system in the Universe. By the observation of the dynamic of systems, we found out if we consider two physical bodies, their momentums are conserved such as their speeds depend on their factor of mass. We called this principle: the Yandza First Law. We have also shown that the density of any system in the Universe stretch(es) to the density of a photon. We called this new principle: Yandza Second Law. On the basis of these two Laws, we have defined the Time as the measure of the interactions between the matter of a physical system and the antimatter produced. By studying these interactions, we discovered a new particle which disintegrates to a photon or an antiphoton according to its environment. We called this particle: particle Y. To conclude this research, we defined the force as the measure of the deformation of the Space-Time like in General Relativity Theory. So, we drawn the lines of force and we discovered the conical shape of the Universe.
- Perez JP. Relativité: Fondements et applications, Dunod, Paris. 2016 ; ISBN 978-2-10-075155-6.
- Perez JP. Thermodynamique : Fondements et applications, Masson, Paris. 1997; 96-116:ISBN 2-225-85572-2.
- Schroeder P. La loi de la gravitation Universelle Newton Euler et Laplace, Springer. 2007. ISBN 978-2-287-72082-6.
- Yandza MJO. A new theory on the shape of the Universe and the origin of the Time, Int J Phys Res Appl. 2022; 5: 001-006.
- De BroglieL. Recherches sur la théorie des quanta, Ph.D. thesis, Migration-université en cours d’affectattion. 1924.
- Solari HG, Natiello M. A constructivist View of Newton’s Mechanics, Springer. 2019. doi: 10.10007/s10699-018-9573-z.
- Haug EG. Newton’s and Einstein’s gravity in a new perspective for Planck masses and smaller sized objects, Int J of Astron and Astrophys. 2018; 8(1): 6-23. doi: 10.4236/ijaa.2018.81002.
- Motohashi H, Minamitsuji M. General relativity solutions in modified gravity, Phys Lett. B781. 2018; 728-734. doi: 10.1016/j.phys let b.2018.04.041.
- Tu Lc, Luo J, Gilles GT. The mass of the photon, Rep on pro in Phys. 2004. doi: 10.1088/0034-4885/68/1/R02.
- Arruga D, Achour JB. Deformed general relativity and quantum black holes interior, Universe. 2020. https://doi.org/10.3390/Universe6030039.
- Newton I. Mathematical Principles of Natural Philosophy. Published by Daniel Adee. 1846. ISBN C037272162.
- Abdel-Raouf M. Novel consequences of coexistence of matter and antimatter in nature. J High Energy Phys Gravitat and Cosmol. 2020; 06:02. doi: 10.4236/jhepgc.2020.62019.
- Goldhaber AS, Nieto MM. New geomagnetic limit on the mass of the photon. Phys Rev Lett. 1968; 21(8):567.
- Franken P. Ampulski, Photon rest mass. Phys Rev Lett. 1971; 26(2):115.
- Ryutov D. Using plasma physics to weigh the photon, Plasma Phys Control Fusion. 2007; 49(12B):429.
- Bonetti L, Ellis J, Mavromatos NE, Sakharov AS. Photon mass limits from fast radio bursts, Phy Lett B. 2016; 757:548-552.
- Bonetti L, Ellis J, Mavromatos NE, Sakharov AS, Frb 121102 casts new light on the photon mass. Phy Lett B. 2017; 768:326-329.
- Coray M, Annavarapu R. Rest mass of photon on the surface of matter, Results Phys. 2020; 16:102866. https: //doi.org/10.1016/j.rinp.2019.102866.
- Hartle JB. General relativity in the undergraduate physics curriculum. Am J Phys. 2006. https://doi.org/10.1119/1.2110581.
- Kanjampatti PO, Pollachi T. Nadu, On freedman equation and the shape of our Universe, Ann of Mathemat Phys. 2020. doi: 10.17352/amp.000015.
- Luminet JP. The shape and topology of the Universe. arXiv. 2008. doi: arXiv: 0802.2236.
- Hojman S. Kuchar K, Teitelboim C. New approach to general relativity. Nat Phys. 1973; 245:97-98. https://doi.org/10.1038/physci245097a0.
- Borchardt G. Infinite Universe theory, Proceedings of the NPA. 2015. doi: 10.13140/RG.2.1.3515.0247.
- Luminet JP, Weeks JR, Riazuelo A, Lehoucq R, Uzan JP. Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background. Nature. 2003 Oct 9;425(6958):593-5. doi: 10.1038/nature01944. PMID: 14534579.