More Information
Submitted: March 30, 2023 | Approved: April 06, 2023 | Published: April 07, 2023
How to cite this article: Usubamatov R. Gyroscope oscillation depends on a rotor speed velocity. Int J Phys Res Appl. 2023; 6: 068-072.
DOI: 10.29328/journal.ijpra.1001053
Copyright License: © 2023 Usubamatov R. This is an open access article distributed under the Creative Commons Attribution License, which peRmits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Gyroscope oscillation depends on a rotor speed velocity
Ryspek Usubamatov*
Department of Automation and Robotics, Kyrgyz State Technical University after I. Razzakov, Kyrgyzstan
*Address for Correspondence: Ryspek Usubamatov, Department of Automation and Robotics, Kyrgyz State Technical University after I. Razzakov, 66 Aitmatov Avenue, 720044, Bishkek, Kyrgyzstan, Email: ryspek0701@yahoo.com; ryspek0701@gmail.com
In engineering, all moving rotating objects exhibit gyroscopic effects resulting from the action of an external torque on a rotating object. Gyroscopic effects are the action of a set of inertial moments and movements of an object around three axes of a three-dimensional Cartesian coordinate system. Moments of inertia are created by centrifugal and Coriolis forces, as well as the moment of change in angular momentum, which is expressed by their kinetic energy. The values of the moments of inertia directly depend on the speed of rotation of the object and its rotation around the axes. A short-term effect of an external load on a running gyroscope with displaced support can be manifested by its oscillations. The physics of gyroscope oscillations is not well explained in publications. This article describes the oscillations of a gyroscope by the action of the external torque which is its potential energy converting into kinetic energy of the inertial torques of the gyroscope. The conversion is carried out by the principle of mechanical energy conservation which is the same as for oscillations of a spring with a load.
Scientific researchers have become interested in the gyroscopic effects of spinning objects at the time of intensive applications of engineering for economics [1]. The gyroscopic effects are generated by the action of the external toque on the spinning object [2,3]. At the earliest stages of the study of gyroscopic effects, researchers intuitively foresaw the action of the inertial forces and toques on the spinning object [4,5]. Only mathematician L. Euler described one gyroscopic effect which is inertial torque presented by the change in the angular momentum [6,7]. The action of other inertial toques and motions of the spinning object remained unexplainable until our time [8,9].
The gyroscopic effects are described by several physical principles which were discovered at different times over several centuries [10-12]. The physics of all gyroscopic effects were analytically explained at our time and published in several manuscripts and one book [13].
The gyroscopic effects of rotating objects are based on several fundamental principles of classical mechanics and manifested several peculiarities. These principles are centrifugal, and Coriolis forces, the change in the angular momentum, and kinetic energy conservation. The action of the inertial torques is correlated by the looped feedback system around axes and expressed by the dependency of velocities rotations of the gyroscope [13]. The set of the inertial torques operating about two axes is presented by four centrifugal and two Coriolis toques, and two torques of the change in the angular momentum. The kinetic energies of the gyroscope around each axis are equal. This property is maintained by the looped feedback system of the action of the inertial torques. The inertial torques are generated by the disc’s moment of inertia, its spinning velocity, and the velocity of the gyroscope rotation around an axis. The inertia torque values drastically depend on the geometry of the disc, its spin velocity, and the velocity of rotation around the axis.
The inertial torques acting around axes were defined by the principles of the theory of gyroscopic effects for rotating objects. The expressions of the inertial torques generated by the spinning disc for horizontal disposal and the dependency of the rotation around axes are shown in Table 1. The table presents the fundamental principles of the theory of gyroscopic effects that enable solving all problems related to the dynamics of rotating objects [14].
Table 1 contains several symbols where ωi is the angular velocity of the disc about axis i; ω is the angular velocity of the spinning disc; J is the moment of inertia of the disc. The digital components of the expressions of inertial torques belong to the spinning disc. Rotating objects of other designs have different digit components. The action of inertial toques is manifested as the resistance to the external toque and as the precession toque with side action relative to the external one.
| Table 1: Fundamental principles of the theory of gyroscopic effects. | |||
| Principles | Forces and torque | Action | Expression |
| Inertial torques of rotating mass | Centrifugal forces | Resistance | |
| Precession | |||
| Coriolis forces | Resistance | ||
| Change in an angular momentum | Precession | ||
| Kinetic energy conservation | Dependency of the angular velocities for the gyroscope rotation around axes | ||
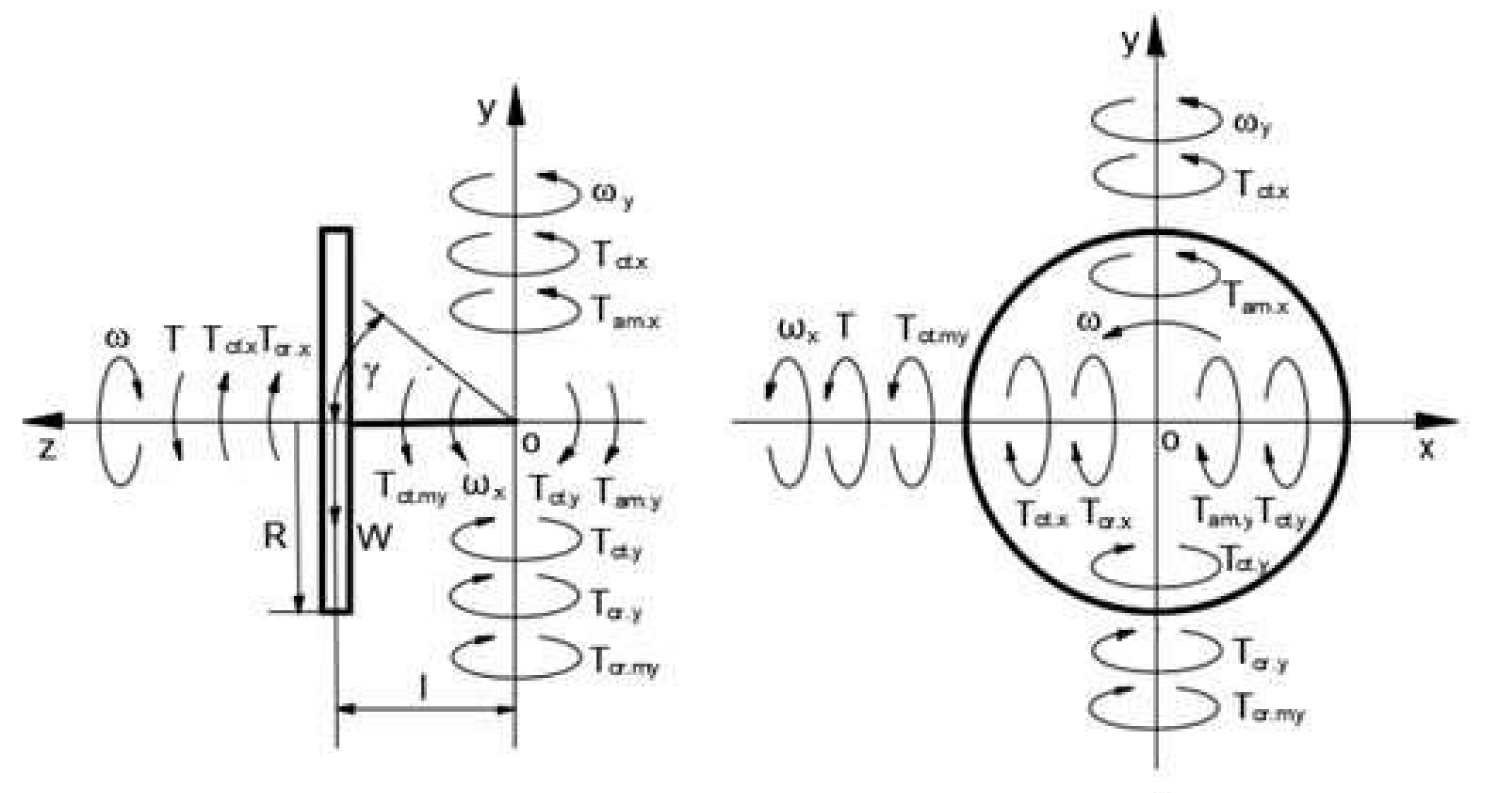
Figure 1: Schematic of acting torques on the gyroscope with one side support.
The mathematical model for the motions of the gyroscope with one side support and the action of the external and inertial torques (Figure 1) was validated by the practical tests. The observation of the gyroscope motion in the laboratory environment demonstrated its oscillation after the short time action of the external torque. The physics of the gyroscope oscillations is not well explained in publications because this process differs from the swinging of the pendulum and other similar objects. This article describes in detail the gyroscope oscillations by the principle of mechanical energy conversion and demonstrates the similarities between the oscillations process of the spring with the load.
The physics of the gyroscope oscillation and analysis of the action of its inertial toques are considered in the example of the motions of the gyroscope with the horizontal disposition (Figure 1). The action of the external torque T produced by the disc weight generates the set of interrelated inertial torques acting around axes ox and oy. The inertial torques acting around the axis ox are the resistance torques that counteract the external torque, T. The inertial torques of axis oy are the precession torques. The action of the resistance and precession torques is interrelated by the dependency of the angular velocities around axes (Table 1) [14]. Inertial torques acting around each axis of the gyroscope contain the torques originating around two axes and present the looped feedback system. The modified expression of the resistance torque Tr.x acting around axis ox is as follows:
(1)
Where all components are as specified in Table 1.
Practically, the gyroscopic disc spins with a high value of angular velocity, which formulate the high value of the inertial torques and hence the high value of the resistance torque Tr.x. The value of the resistance torque (Eq. (1)) is always less than the value of the external torque T and opposite in action on the gyroscope. The resistance torque Tr.x is the restraining torque. The action for the external torque T forms the direction of the angular velocity ωx of the gyroscope motion. The expression of the inertial torque contains the product ωωx whose value is constant and expresses the kinetic energy of the gyroscope motions. The angular velocity ω expresses the kinetic energy of the spinning disc. The angular velocity ωx expresses the kinetic energy of the gyroscope motion around the axis ox, which is the result of converting the potential energy of the gyroscope weight into its kinetic energy of motion. The constant product ωωx expresses the principle of mechanical energy conservation. For the accepted system of the gyroscope energy, it means the increase in the speed ω of the disc will lead to a decrease in the angular velocity ωx of the gyroscope rotation around an axis ox and vice versa.
Practical tests of the short-time action of the external toque on the gyroscope demonstrate two types of its motions. First, if the gyroscope runs with the high-speed rotation of the disc, it shifts the disposition without return. The second, for the low-speed rotation of the disc, the gyroscope demonstrates oscillated motions. The physics of these motions should be considered in detail and compared with the physics of other objects that demonstrate similar behavior after the action of the external load. The comparative analog can be the strain spring with the load which manifests oscillation and overdamped property that depends on its stiffness. There are differences in their properties like inertial torques of the spinning disc do not possess the property of the spring’s torque and do not have the index of the spring stiffness and others. Comparative analysis of the gyroscope and spring properties can clarify the differences and show the physical unity of these processes.
Analysis of the gyroscope and the strain spring with high values of the physical properties shows the following.
- The external torque acting on the gyroscope with the high speed of the disc generates the resistance inertial toques of the high value and the small value angular velocity of its rotation around axis ox (Figure 1). The resistance inertial toques are the potential energy.
- The spring of high stiffness produces the resistance force of the high value and small flexible deformation under the action of the load. The resistance force of the spring is the potential energy
- The high speed of the gyroscope’s disc and the high stiffness of the spring are resulted in the high values of the resistance torque and force, accordingly. The gyroscope and the spring do not manifest the oscillations because they are of the overdamped property.
- The low angular velocity of the gyroscope’s disc and the small stiffness of the spring resulted in the low values of the resistance torque and the big value of the flexible deformation, respectively. The gyroscope and the spring manifest the oscillations.
- The external load of the short-time action shifts the gyroscope to the new position because its value is over than the resistance toque of the inertial toques. The gyroscope will run the new conditions.
- The strain spring will receive plastic deformation under the action of the external load and will lose the initial property.
Analysis of the gyroscope and the strain spring with low values of the physical properties shows the following.
- The external torque acting on the gyroscope with the low speed of the disc generates the resistance inertial toques of the low value and the high-value angular velocity of its rotation around the axis ox (Figure 1).
- The spring of low stiffness produces the resistance force of the low value and large flexible deformation under the action of the load.
- The low speed of the gyroscope’s disc and low stiffness of the spring resulted in the low values of the resistance torque and force, accordingly, and the large angular velocity of rotation and the large flexible deformation, respectively. The gyroscope and the spring manifest the oscillations property.
The gyroscope oscillation is considered in terms of machine dynamics and vibration analysis [6,7]. The simulation of a free oscillation is represented by principles of mechanical energy conservation. The oscillations of the spinning disc continually convert part of its kinetic energy into work and are dynamically irreversible manifested in the damping process. The change in the kinetic energy leads to the change in the inertial torques and the velocities of the disc around the axes of rotation. These changes are manifested by the monotonic decay of the spinning disc oscillation.
The amplitudes of oscillated motions of the spinning disc are defined by the principles of mechanical energy conservation. The weight of the disc and external torque of the short –time action expresses the potential energy. The inertial torques of the spinning disc express its kinetic energy. The total mechanical energy of the spinning disc is constant and equal at any point of the oscillation and is presented by the following expression:
(2)
where Pi is the potential energy of the disc weight on the angle γi; ΣKi is the kinetic energy of the disc mass motion about the point of rotation; ΣAi is the work of the inertial torques at the angle of spinning disc turn; the sign (±) is applied for the work that coincides or is opposite to the action of the disc weight.
The product ωωx that is the component of the inertial torque expressions discussed above gives information about the gyroscope amplitude of the oscillation. The kinetic energy of the gyroscope inertia torques is limited by the maximal value of the product (ωωx)*, which depends on the value of the disc speed ω. The value of the gyroscope axial rotation ωx also depends on the value ω. The components ω and ωx, enable showing the value of the amplitude of the gyroscope oscillation. The low-value ω of the disc spin gives the high-value ωx of its rotation about the axis ox, which product should not exceed the maximal value of the product (ωωx)*. For the given value of the disc spin ω, the value of the gyroscope axial rotation ωx is a variable in which time action yields ωxt = γ the angle of the amplitude of the gyroscope oscillation.
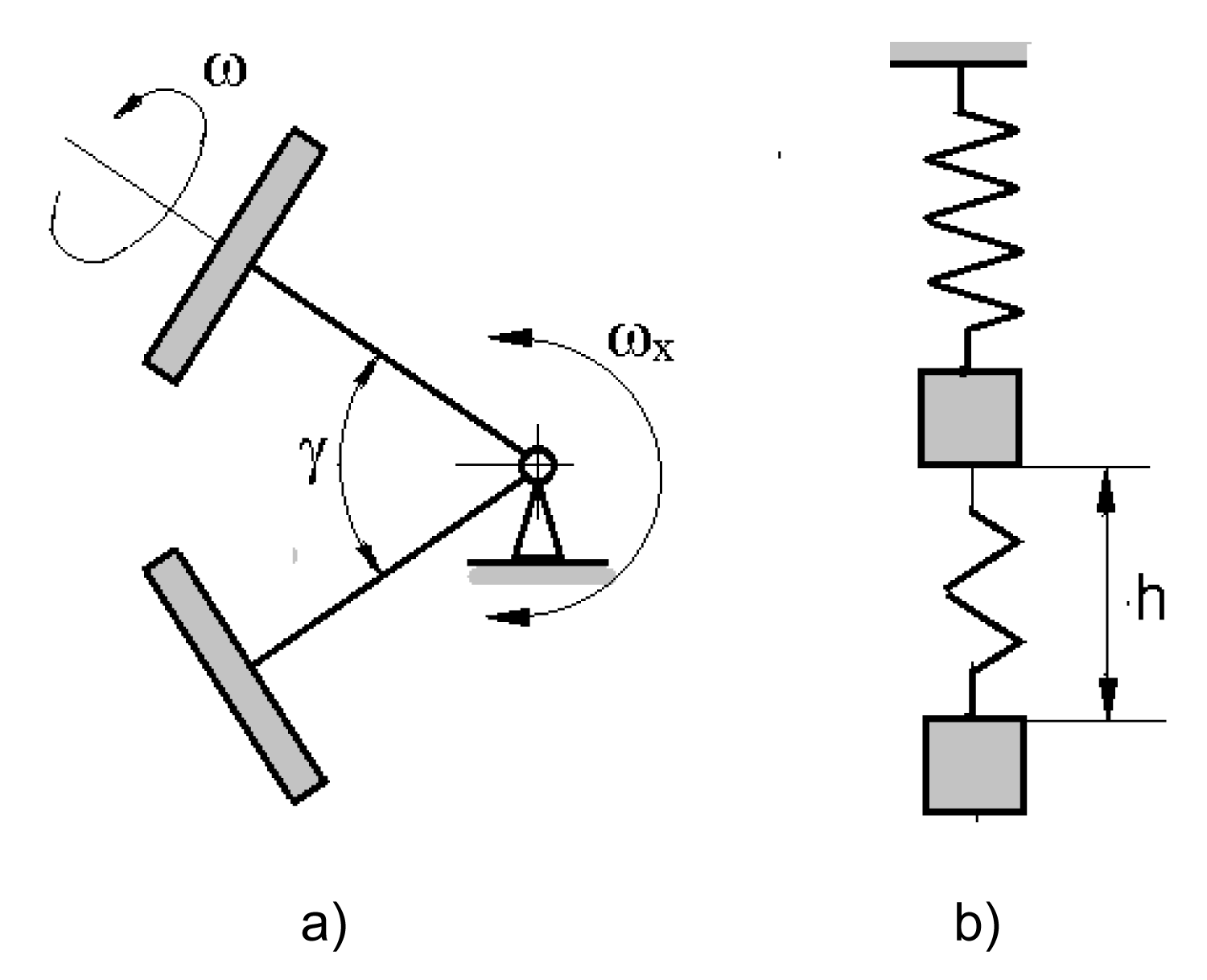
The value of the resistance torque of the gyroscope with a low angular velocity of the disc spin ω is increased by the increase of the value of the gyroscope axial rotation ωx. It is increased by the short-time action of the external torque on the gyroscope. The high value of the resistance torque turns up the gyroscope until its value is nullified because the angular velocity ωx = 0 due to the action of the gyroscope weight. The inertial force continues to turn up the gyroscope which resistance toque begins to act in opposite direction and the gyroscope turns down. The angle γ of the gyroscope disposition between the lowest and highest points is presented in the amplitude of its oscillation (Figure 2a).
Figure 2: Oscillation of a gyroscope (a) and a strain spring (b).
Similar discussions can be presented for the oscillations of the strain spring with the load, the spring stiffness, flexible deformation, and connection with the amplitude of oscillations. The external load of the short-time action on the spring with the load will shift it down with the increase in the resistance force of the spring due to its strain. The high value of the spring force will lift the load and the spring reaches the neutral disposition where its resistance force is nullified. The load continues to lift due to the action of the inertial force and the spring begins squeezing and increasing the value of the spring resistance force. The motion of the load is ending and the spring resistance force pushes down the load. The spring dispositions between the lowest and highest points present the amplitude h of its oscillation (Figure 2b).
Analysis of the physical peculiarities of the gyroscope and the strain spring shows the short - time action of the external load on the gyroscope and the spring demonstrate similar properties. The action force on the spring and torques on the gyroscope and their motions are a demonstration and the manifestation of the one physical principle, which is mechanical energy conservation. The indices of the gyroscope properties and meaning which express the indices of the strain spring and its terms are presented in Table 2.
| Table 2: Indices of the gyroscope and the strain spring. | ||
| Property | Strain spring | Gyroscope |
| Indices | ||
| Stiffness | k | ω;ωx |
| Flexible deformation |
l | ω;ωx |
| Amplitude | h | ω;ωx |
The oscillation processes of the strain spring with the weight and the gyroscope with one side support are accomplished by one physical principle. The oscillation processes of the strain spring are well described in the textbooks and other publications. The gyroscope oscillation processes are presented only by intuitive assumptions without mathematical modeling. The gyroscopic effects for rotating objects enable ascertaining the components of the gyroscope motions that express the meaning of the spring indices for the oscillation processes. The known strain spring indices can be presented by the indices of the gyroscope motions that reflect on the oscillation processes (Table 2).
The oscillation processes of the strain spring with the weight depend mainly on the stiffness k of the spring. Other indices as the flexible deformation l of the spring and the amplitude h of oscillation depend on the spring stiffness and the values of the weight, external load, and the time of its action. The oscillation processes of the gyroscope depend mainly on the value of its disc angular speed ω. Other indices as the angular velocity ωx of the gyroscope rotation around an axis and the amplitude of oscillation depending on the disc angular speed and the values of the gyroscope weight, external load, and the time of its action.
The similarities in the indices and properties of the oscillation processes for the gyroscope with one-side support and the strain spring with the load are obvious. The physical processes of the oscillation for the gyroscope and the spring are different. The commonality of the oscillation processes of different natures is explained and described by the mechanical energy conservation law (Eq. (2)).
The oscillation process of the gyroscope with on-site support is the result of the short-time action of the external torque, inertial torques generated by the spinning disc, and the weight of the gyroscope. The potential energy of the external torque of the short-time action is converted into the kinetic energy of the gyroscope motions around axes of rotation. The component of the inertial torques, which is the product ωωx of the disc speed ω and its rotation ωx around the axis, expresses the kinetic energies of the spinning disc. The kinetic energy of the gyroscope inertial torques is limited by the maximal value of the product (ωωx)*, which mainly depends on the value of the disc speed ω. The gyroscope with the high value of the disc spin ω does not manifest the oscillation because of the small value of the velocity rotation ωx about the axis of oscillation. The value of the disc spin ω forms the value of the velocity rotation ωx and the value of the amplitude of the gyroscope oscillation. The value of the resistance torque of the gyroscope is decreased by the decrease of the value of the disc spin ω which leads to an increase in the value of the velocity rotation ωx and the value of the amplitude of the gyroscope oscillation.
The presented analysis of the gyroscope oscillation was conducted based on the theory of gyroscopic effects that was validated by the physical tests for the gyroscope motions. Gyroscope oscillations are a complex dynamic process with motions around axes. Practical tests of the gyroscope oscillations are entailed with limitations in measuring torque values and the time of the action. Such tests need high-tech instrumentations and qualified laboratory staff. Conducted analysis was focused on the physics of oscillations, the action of the inertia torques, and defining similarities with the spring oscillations.
The presented analysis of the gyroscope oscillation is the first theoretical approach that considers the oscillation around one axis. The action of the torques considered is analyzed in terms of potential and kinetic energies. In reality, gyroscope oscillation is a complex task with the action of the inertial torques around two axes and with their partial deactivation. The quantitative example of the simplified theoretical analysis does not describe the physics of the gyroscope oscillation but opens the right direction for research. Future research should be conducted on the spatial oscillation processes of the spinning disc and validation by the technically equipped tests.
The oscillation process of the gyroscope with on-site support is one type of gyroscopic effect that is the result of the action of the external torque on the spinning object. The physics of the gyroscope oscillations is not well described in publications. The oscillations of a gyroscope express the conversion of the potential energy of the action of the external torque into the kinetic energy of the inertial torques of the gyroscope. The conversion is carried out by the principle of mechanical energy conservation. The theory of the oscillation for the strain spring with a load is the same as for the gyroscope oscillations. There are similarities in the indices and properties of the oscillation processes for the gyroscope with one-side support and the spring. The physics of the oscillation for the gyroscope and the spring have based on the common principle of mechanical energy conservation.
- Cordeiro FJB. The Gyroscope. Createspace, NV, USA. 2015.
- Greenhill G. Report on Gyroscopic Theory. Relink Books, Fallbrook, CA, USA. 2015.
- Hibbeler RC, Yap KB. Mechanics for Engineers-Statics and Dynamics. 13th ed. Prentice Hall, Pearson, Singapore. 2013.
- Scarborough JB. The Gyroscope Theory and Applications. Nabu Press, London. 2014.
- Smith PF, Longley WR. Theoretical Mechanics. Franklin Classics, Boston. 2018.
- Nolting W. Theoretical Physics 1: Classical Mechanics. Springer, Cham, Switzerland. 2016.
- Taylor JR. Classical Mechanics. University Science Books, California, USA. 2005.
- Weinberg H. Gyro Mechanical Performance: the most important parameter. Analog Devices. Technical Article MS-2011; 2158: 1-5.
- Aardema MD. Analytical Dynamics. Theory and Application. Academic/Plenum Publishers, New York. 2005.
- Baumann G. Mathematica for Theoretical Physics. Springer, New York. 2003.
- Dreizler R. Theoretical Mechanics: Theoretical Physics 1. Springer, Boca Raton. 2010.
- Russell K, Shen Q, Sodhi RS. Kinematics and Dynamics of Mechanical Systems. 2nd ed.: Implementation in MATLAB and SimMechanics, Taylor & Francis, Boca Raton. 2019.
- Usubamatov R. Allen D. Corrected inertial torques of gyroscopic effects. Advances in Mathematical Physics. 2022; 2022: 3479736.
- Usubamatov R. Theory of Gyroscope Effects for Rotating Objects. 2nd ed. Springer, Cham, Switzerland. 2022.