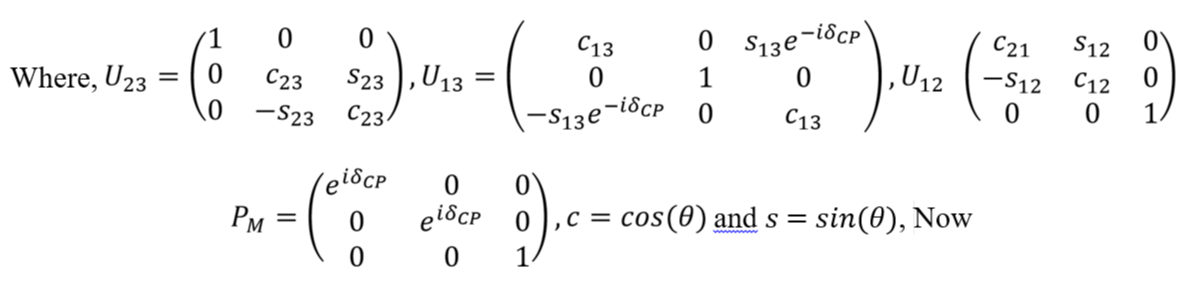Oscillation of neutrino in a vacuum with mixing flavor

We developed multiple equations to observe the two and three flavors of neutrino oscillation with the mixing angle based on L/E=0.1 to 0.9 in this study. In different settings, the nature of the neutrino oscillation probability was discovered to be varied in different equations. The observation indicates increasing likelihood in one equation and decreasing probability in the other equations in two flavor oscillation neutrinos. To characterize the probability of neutrino oscillation, we use four distinct angles: 50, 100, 150, and 200. The probability of neutrino oscillation was determined to be highest at an angle of 150 degrees. However, with increasing mixing angles, the likelihood of oscillation increases on the basis of created equation (25) and decreases on the basis of equations (26) and (27) in the three-flavor neutrino oscillation. From generated equations (25) and (26) the maximum neutrino oscillation of probability is discovered at an angle of 150, however, from equation (27), the maximum probability is observed at 50. The greatest neutrino oscillation is found to be 0.9999 and the minimum is zero in all of these two and three flavors of oscillation.

Neutrino physics is one of the most fascinating and hotly debated issues in today’s high-energy physics. The question of whether neutrinos can oscillate or not prompted a slew of tests to see if these oscillations might be observed. The number of electron neutrinos detected from the sun is 2-3 times lower than the number expected by the mainstream solar model (SSM). Because neutrinos have no mass and hence cannot oscillate in the standard model of particle physics, their measurement reveals the existence of novel physics beyond the SM. The neutrino masses and the entries in the neutrino mixing matrix are two of the unknown parameters. Giunti, Kim, and Lee first estimated the oscillation probability for neutrinos in a wave packet model, then demonstrated that the state vectors utilized for quantum mechanical description and developed a theoretical framework in quantum field in 1993. Finally, in 1995, Blasone and Vitiello demonstrated that the quantum field theory (QFT) description of mixed particles causes unexpected complications in the interpretation of neutrinos as particles. All of the different ways are still being debated today, but under the premise of relativistic neutrinos with minuscule mass squared variations, all of them get the same outcome. For the two flavour case the possibilities of oscillation is given by

$P\mathrm{<mo\; stretchy="false">(</mo>}\alpha \to \alpha \mathrm{<mo>;</mo>}L\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}-si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}\theta \mathrm{<mo\; stretchy="false">)</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>1.27}\frac{\Delta m^{2}L}{E}\mathrm{<mo\; stretchy="false">)</mo>}$ (1)

$P\mathrm{<mo\; stretchy="false">(</mo>}\alpha \to \beta \mathrm{<mo>;</mo>}L\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}-si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}\theta \mathrm{<mo\; stretchy="false">)</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>1.27}\frac{\Delta m^{2}L}{E}\mathrm{<mo\; stretchy="false">)</mo>}$ (2)

Where $\Delta m^2$ is the difference in squared masses as $\Delta m^2=m_i^2-m_j^2$ and the factor of 1.27 is due to the conversion between units. The neutrinos’ energy is E, and the distance between source and detector is L. NO experiments can only measure relative masses, not absolute masses. The oscillation length is defined as $L^{OSC}\mathrm{<mo>=</mo>2.47}$ $\frac{E}{\Delta m^2}$ , which is the distance between complete oscillations. The length of the oscillation imposes a significant constraint on the measurement conditions. Because there are no oscillations for if L ≈ L_osc and the oscillations for L≪L^osc are averaged out due to natural uncertainties for the neutrino energy, the oscillations can only be detected if L≫L^osc. As a result, the NO condition is $\frac{\Delta m^{2}L}{2E}$ ≈ 1 [1]. In quantum physics, state vectors are used to characterize flavor neutrinos and are commonly used to define mixing in terms of state vectors.

${\nu }_{\alpha }\mathrm{<mo>:</mo><mo>=</mo>}{\displaystyle \sum _i}{U}_{\alpha i}^{\mathrm{<mo>*</mo>}}{\nu }_i$ (3)

Equivalently, the same can be done for the anti-particle state vectors, which is defined as

${\overline{\nu }}_{\alpha }\mathrm{<mo>:</mo><mo>=</mo>}{\displaystyle \sum _i}{U}_{\alpha i}^{\mathrm{<mo>*</mo>}}{\overline{\nu }}_i$ (4)

The formulations of state vectors in (3) and (4) are the most frequent, and they are used in most quantum mechanics studies dealing with neutrino oscillations. When comparing (3) and (4), it is clear that the difference in neutron and anti-neutrino therapy is just a complex conjugation of the PMNS-matrix. The degrees of freedom for space-time, as well as the energy-momentum relationship and the degree of freedom that distinguishes the neutrino species, must be factorized. Furthermore, quantum mechanics converts the general wave function of a spin-1/2 particle into a spin-independent wave function and a spin vector.

$\psi \mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{,}\sigma \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\psi }_{\uparrow }\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}\left(\begin{array}{c}1\\ 0\\ \end{array}\right)+{\psi }_{\downarrow }\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}\left(\begin{array}{c}0\\ 1\\ \end{array}\right)$ (5)

This leads to a factorization of the Hilbert space into two parts

$\mathscr{H}\mathrm{<mo>=</mo>}{L}^2\underset{}{{\displaystyle \otimes }}{\mathcal{C}}^2$ (6)

Because the space-time and energy-momentum degrees of freedom for a flavor neutrino are a priori unknown, this type of factorization is only viable for mass neutrinos. The entire Hilbert space for neutrinos can be expressed as a direct product of the ${\mathscr{H}}_d=\text{L}{ }^2$ space for dynamical degrees of freedom and the ${\mathscr{H}}_m={\mathcal{C}}^{N_m}$ space for mass degrees of freedom;

$\mathscr{H}\mathrm{<mo>:</mo><mo>=</mo>}{\mathscr{H}}_d\underset{}{{\displaystyle \otimes }}{\mathscr{H}}_d\mathrm{<mo>=</mo>}{L}^2\underset{}{{\displaystyle \otimes }}{\mathcal{C}}^{N_m}$ (7)

The state vectors described in above equation (3) can be used as a basis for ${\mathscr{H}}_m$ , the elements of ${\mathscr{H}}_d$ will be denoted by ${\psi }_i$ ,

where the index i indicates the mass dependence of the dynamics.

Neutrinos have no mass in the most basic version of the SM. In fact, because neutrino masses are so much less than the masses of the other fermions, this has been a pretty good representation of Nature for a very long time. Adding neutrino masses via connecting neutrinos to the Higgs field, which would give birth to neutrino masses in the same way as other fermion masses, appears to be the most tempting method at first appearance. Some fermions are referred to as Majorana fermions since they lack their own anti-particle, which is referred to as a Dirac fermion. There have been no observations to yet that have been able to determine whether neutrinos are Dirac or Majorana fermions, which is one of the most intriguing potentials for future neutrino studies. Basic concepts of neutrino oscillations are if neutrinos are massive, then they will oscillate which means their reaction occur with charged lepton of a given generation. The probability for the oscillation of a neutrino of a given generation into a neutrino of another given generation can be calculated to be dependent on the difference between the squares of the neutrino masses. Thus, if neutrinos are massless, or if they all have the same mass, then they will not oscillate. It follows that if neutrino oscillations are observed, then neutrinos must be massive with at least two different masses. In addition to this, there must also be mixing in the lepton sector as the amount of mixing will determine the oscillation amplitudes.

The fundamental principle of neutrino oscillations is that if neutrinos are heavy, they will oscillate, which indicates that their reaction will take place with a charged lepton of a certain generation. The difference in the squares of the neutrino masses can be used to compute the chance of a neutrino of one generation oscillating into a neutrino of another generation. As a result, if neutrinos have no mass or have the same mass, they will not oscillate. If neutrino oscillations are detected, then implies that neutrinos must be hefty, having at least two distinct masses. Furthermore, mixing in the lepton sector is required, as the quantity of mixing determines the oscillation amplitudes.

Neutrino oscillations in vacuum

Let us consider how flavors mixing affects the propagation of neutrinos in vacuum and initial state to be the flavors eigenstate is given as,

${\nu }_{\alpha }\mathrm{<mo\; stretchy="false">(</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{U}_{\alpha j}^{\mathrm{<mo>*</mo>}}{\nu }_j$ (8)

The flavor eigenstates are denoted by e, µ, τ and mass eigenstates 1, 2, 3. Then after traveling certain distance the state of neutrino is given as

$\nu \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{U}_{\alpha j}^{\mathrm{<mo>*</mo>}}{e}^{-i\mathrm{<mo\; stretchy="false">(</mo>}{E}_{j}t-p_{j}x\mathrm{<mo\; stretchy="false">)</mo>}}{\nu }_j$ (9)

Here, $E_j$ and $p_j$ are the energy and momentum associated with the mass eigenstate j. They can be derived from the dynamics of the elementary process in which the neutrino is produced. For example, in the case of pion decay at rest, π+ → µ+ + νµ or π− → µ− + vµ, the center of mass system can be obtained as,

$m_{\pi }\mathrm{<mo>=</mo>}{E}_j+E_{\mu }\mathrm{<mo>=</mo>}\sqrt{m_j^2+p_j^2}+\sqrt{m_{\mu }^2+p_{\mu }^2}$ (10)

$p_{\mu }\mathrm{<mo>=</mo>}-p_j$ (11)

Substituting equation (10) into equation (11) and taking the square and solving to obtain,

$m_{\pi }^2\mathrm{<mo>=</mo>}{m}_j^2+p_j^2+m_{\mu }^2+p_{\mu }^2+2\sqrt{m_j^2+p_j^2}\sqrt{m_{\mu }^2+p_{\mu }^2}$ (12)

On solving and arranging we get,

$p_j^2\mathrm{<mo>=</mo>}\frac{m_{\pi }^2}{4}{\mathrm{<mo\; stretchy="false">(</mo>1}-\frac{m_{\mu }^2}{m_{\pi }^2}\mathrm{<mo\; stretchy="false">)</mo>}}^2-\frac{m_j^2}{2}{\mathrm{<mo\; stretchy="false">(</mo>1}-\frac{m_{\mu }^2}{m_{\pi }^2}\mathrm{<mo\; stretchy="false">)</mo>}}^2+\frac{m_j^4}{4m_{\pi }^2}$ (13)

$E_j^2\mathrm{<mo>=</mo>}\frac{m_{\pi }^2}{4}{\mathrm{<mo\; stretchy="false">(</mo>1}-\frac{m_{\mu }^2}{m_{\pi }^2}\mathrm{<mo\; stretchy="false">)</mo>}}^2-\frac{m_j^2}{2}{\mathrm{<mo\; stretchy="false">(</mo>1}-\frac{m_{\mu }^2}{m_{\pi }^2}\mathrm{<mo\; stretchy="false">)</mo>}}^2+\frac{m_j^4}{4m_{\pi }^2}$ (14)

By denoting the energy that would be obtained for massless neutrinos by $\text{E= }{m}_{\pi }^2\text{ (1-}\frac{m_{\mu }^2}{m_{\pi }^2}\text{ )}$ and keeping only terms up to second order in $m_j$ , the momentum and energy is obtained as,

$p_j^2\mathrm{<mo>=</mo>}E-\frac{m_j^2}{2E}\mathrm{<mo\; stretchy="false">(</mo>}\frac{1}{2}-\frac{m_{\mu }^2}{m_{\pi }^2}\mathrm{<mo\; stretchy="false">)</mo>}$ (15)

$E_j^2\mathrm{<mo>=</mo>}E+\frac{m_j^2}{2E}\mathrm{<mo\; stretchy="false">(</mo>1}-\mathrm{<mo\; stretchy="false">[</mo>}\frac{1}{2}+\frac{m_{\mu }^2}{m_{\pi }^2}\mathrm{<mo\; stretchy="false">]</mo><mo\; stretchy="false">)</mo>}$ (16)

Now, the neutrino oscillation probability is obtained [2] as,

$P\mathrm{<mo\; stretchy="false">(</mo>}{\nu }_{\alpha }\to {\nu }_{\beta }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo><mo>|</mo>}{\nu }_{\beta }{\nu }^2\mathrm{<mo>=</mo><mo>|</mo>}{U}_{\beta j}{U}_{\alpha j}^{\mathrm{<mo>*</mo>}}{e}^{-i\frac{m_j^{2}t}{2E}}{\mathrm{<mo>|</mo>}}^2$ (17)

Two-flavor oscillations in vacuum

Now to study the oscillation of two flavor neutrino we consider ${\nu }_e$ and ${\nu }_x$ initially which is successful in describing many neutrinos oscillation experiments. In two flavors, there are no Dirac phases, implying that the lepton mixing matrix is real, and the only parameters are the mixing angle (𝜃) and the mass squared difference $\mathrm{<mo\; stretchy="false">(</mo>}\Delta m^2\equiv m_2^2-m_1^2\mathrm{<mo\; stretchy="false">)</mo>}$ . Now the lepton mixing matrix for 2D rotation is given as,

$U\mathrm{<mo>=</mo>}\left(\begin{array}{cc}cos\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}& sin\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}\\ -sin\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}& cos\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}\\ & \end{array}\right)$ (18)

On substituting the value of U in general equation of neutrino oscillation probabilities in equation (17) and solving we get, the two-flavor neutrino oscillation probabilities as,

$P_{ee}\mathrm{<mo>=</mo>1}-si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}\theta \mathrm{<mo\; stretchy="false">)</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>}\Delta \mathrm{<mo>/</mo>2<mo\; stretchy="false">)</mo>}$ (19)

$P_{ex}\mathrm{<mo>=</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}\theta \mathrm{<mo\; stretchy="false">)</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>}\Delta \mathrm{<mo>/</mo>2<mo\; stretchy="false">)</mo>}$ (20)

Here, oscillation phase is $\Delta \mathrm{<mo>=</mo>}\frac{\Delta m^{2}L}{2E}$ and can be written as $\frac{\Delta }{2}\mathrm{<mo>=</mo>}\frac{\pi L}{L^{OSC}}$ . In addition, unitarity condition basically states that no neutrinos are lost during the neutrino evolution

Neutrino oscillation in vacuum for three flavor

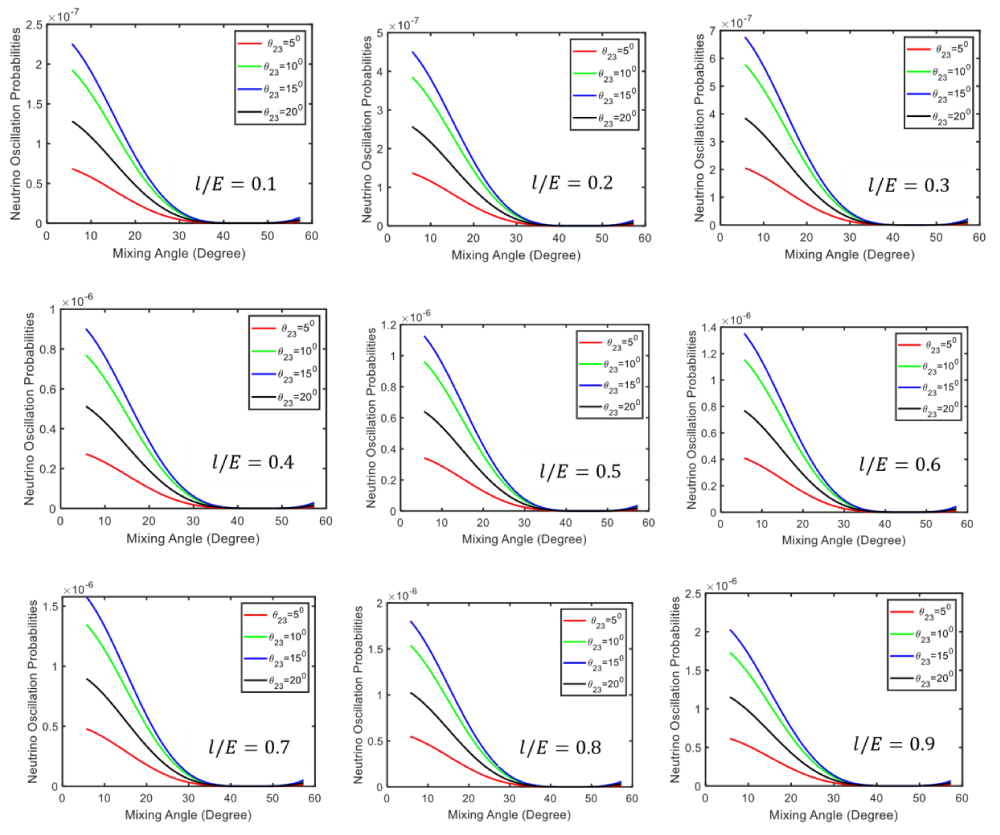
Three-flavor oscillations the lepton mixing matrix using the standard parametrization with three mixing angles and one CP-violating phase. In addition, there will be two independent mass squared differences, $\Delta m_{21}^2$ and $\Delta m_{31}^2$ . $U_{MNO}$ is a 3 x 3 matrix analogous to the CKM matrix for the quarks but due to the Majorana nature of the neutrinos it depends on six independent parameters as,

$U_{MNO}\mathrm{<mo>=</mo>}{U}_{23}{U}_{13}{U}_{12}{P}_M$ (21)

$U_{MNO}\mathrm{<mo>=</mo>}\left(\begin{array}{ccc}1& 0& 0\\ 0& c_{23}& s_{23}\\ 0& -s_{23}& c_{23}\\ & & \end{array}\right)\left(\begin{array}{ccc}{c}_{13}& 0& s_{13}{e}^{-i{\delta }_{CP}}\\ 0& 1& 0\\ -s_{13}{e}^{-i{\delta }_{CP}}& 0& c_{13}\\ & & \end{array}\right)\left(\begin{array}{ccc}{c}_{21}& s_{12}& 0\\ -s_{12}& c_{12}& 0\\ 0& 0& 1\\ & & \end{array}\right)\left(\begin{array}{ccc}{e}^{i{\eta }_1}& 0& 0\\ 0& e^{i{\eta }_2}& 0\\ 0& 0& 1\\ & & \end{array}\right)$ (22)

Where $c_{ij}=cos{\theta }_{ij}$ and $s_{ij}\mathrm{<mo>=</mo>}$ 𝑠𝑖𝑛 𝜃. The angles 𝜃𝑖𝑗 can be taken without loss of generality to lie in the first quadrant, 𝜃𝑖𝑗 ∈ [0,𝜋/2] and the phases 𝛿𝐶𝑃, 𝜂𝑖 ∈ [0, 2𝜋].

$\mathrm{.}{U}_{MNO}\mathrm{<mo>=</mo>}\left(\begin{array}{ccc}{c}_{12}{c}_{13}& s_{12}{c}_{13}& s_{13}{e}^{-i{\delta }_{CP}}\\ -s_{12}{c}_{23}-c_{12}{s}_{13}{s}_{23}{e}^{-i{\delta }_{CP}}& c_{12}{c}_{23}-s_{12}{s}_{13}{s}_{23}{e}^{i{\delta }_{CP}}& c_{13}{s}_{23}\\ s_{12}{s}_{23}-c_{12}{s}_{23}{c}_{23}e& & \end{array}\right)$ (23)

$\left[\begin{array}{c}{\nu }_e\\ {\nu }_{\mu }\\ {\nu }_{\tau }\\ \end{array}\right]\mathrm{<mo>=</mo>}U\left[\begin{array}{c}{\nu }_1\\ {\nu }_2\\ {\nu }_3\\ \end{array}\right]$ (24)

Since there is no direct evidence of non-zero neutrino mass from the laboratory experiments. So, the upper limits from direct kinematic neutrino mass measurements are given as $m_{{\nu }_e}\le 15eV$ , $m_{{\nu }_{\mu }}\le 0.17MeV$ , $m_{{\nu }_{\tau }}\le 18.2MeV$ [4-5]. Now, the neutrino oscillation probabilities for three flavors using UNO in equation (17) obtained as

$P\mathrm{<mo\; stretchy="false">(</mo>}{\nu }_e\to {\nu }_{\mu }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}{\theta }_{13}\mathrm{<mo\; stretchy="false">)</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}{\theta }_{23}\mathrm{<mo\; stretchy="false">)</mo>}sin\mathrm{<mo\; stretchy="false">(</mo>}\frac{\Delta m_{atm}^{2}L}{4E}\mathrm{<mo\; stretchy="false">)</mo>}$ (25)

$P\mathrm{<mo\; stretchy="false">(</mo>}{\nu }_{\mu }\to {\nu }_{\tau }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}{\theta }_{23}\mathrm{<mo\; stretchy="false">)</mo>}co{s}^4\mathrm{<mo\; stretchy="false">(</mo>2}{\theta }_{13}\mathrm{<mo\; stretchy="false">)</mo>}sin\mathrm{<mo\; stretchy="false">(</mo>}\frac{\Delta m_{atm}^{2}L}{4E}\mathrm{<mo\; stretchy="false">)</mo>}$ (26)

Now we will calculate the survival probability of muon neutrinos; that is,

$P\mathrm{<mo\; stretchy="false">(</mo>}{\nu }_{\mu }\to {\nu }_{\mu }\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}-si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}{\theta }_{13}\mathrm{<mo\; stretchy="false">)</mo>}si{n}^2\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_{23}\mathrm{<mo\; stretchy="false">)</mo>}+si{n}^2\mathrm{<mo\; stretchy="false">(</mo>2}{\theta }_{23}\mathrm{<mo\; stretchy="false">)</mo>}co{s}^4\mathrm{<mo\; stretchy="false">(</mo>}{\theta }_{13}\mathrm{<mo\; stretchy="false">)</mo>}sin\mathrm{<mo\; stretchy="false">(</mo>}\frac{\Delta m_{atm}^{2}L}{4E}\mathrm{<mo\; stretchy="false">)</mo>}$ (27)

Two flavor oscillation

The numerical analysis is based on ∆ = 0.1 and the nature is shows in Figure 1. The Figure 1, shows that the probability of neutrino oscillation with the mixing angles. In the case of equation (19) when the ∆ = 0.1, the probability of neutrino oscillation decreases with increasing the mixing angles. The maximum probability of oscillation is approximately 0.99998 at the mixing angle of 5 degree. The neutrino oscillation probability gradually decreases and becomes minimum at the angle of 45 degree after that the probability is certainly increases with increasing the mixing angle and becomes maximum at the angle of 58 degree. In the case of equation (20) when the ∆ = 0.1, the probability of neutrino oscillation is increases with increasing the mixing angles. The maximum probability of oscillation is 2.5×10^-3 at the mixing angle of 45 degree. The neutrino oscillation probability gradually increases from 0.1 to 2.5×10^-3 and becomes maximum at the angle of 45 degree after that the probability is certainly decreases with increasing the mixing angle and becomes minimum at the angle of 58 degree.

Three flavor oscillation

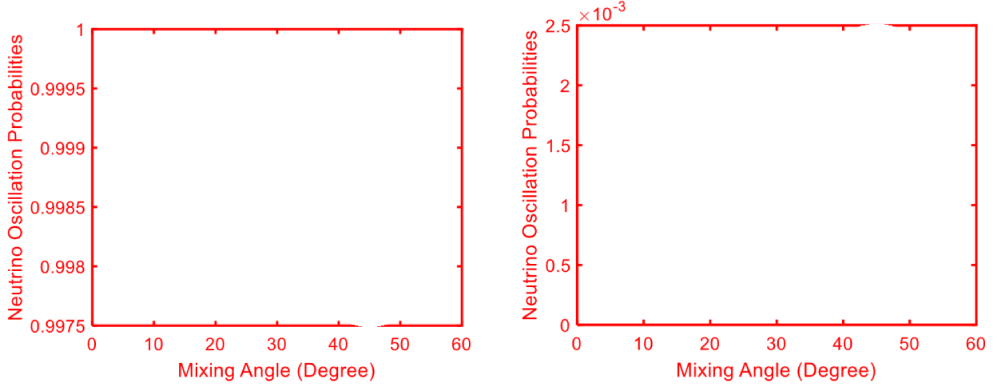
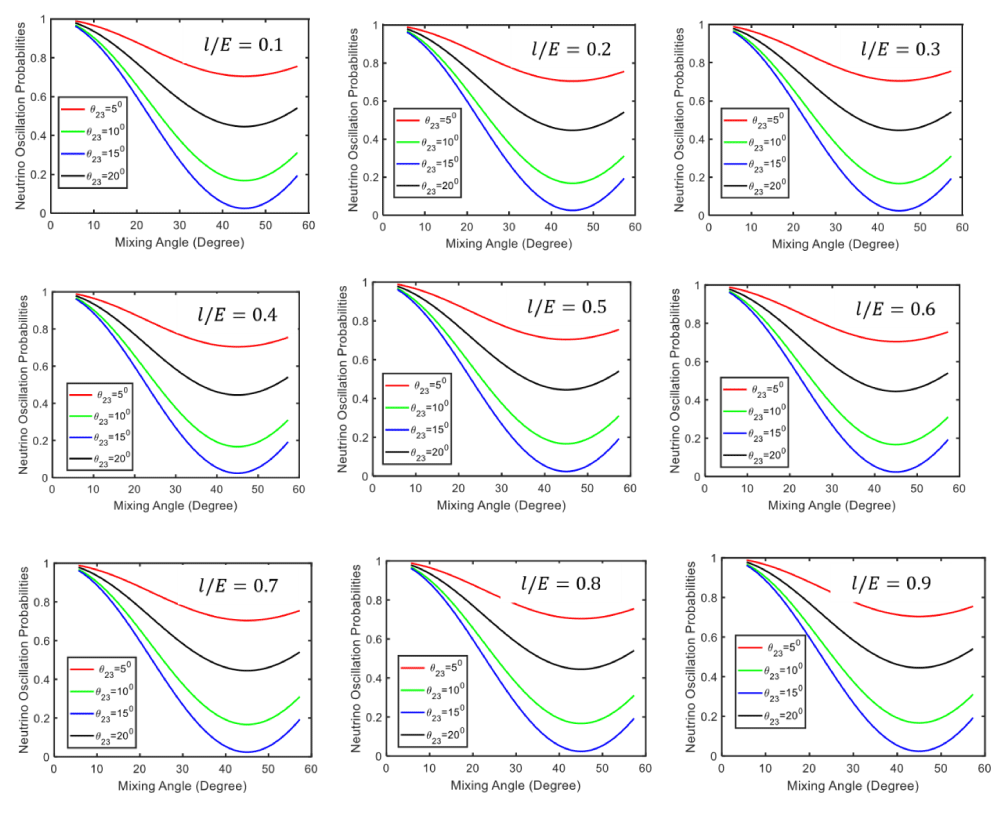
The numerical analysis of developed equation (25) is based on Δ𝑚² = 10⁻⁵𝑒𝑉 with consider 𝜃₂₃ and L/E=0.1 to 0.9 and the nature is shows in Figure 2. In the Figure 2, we clearly see the nature of the neutrino oscillation probability based on Δ𝑚² = 10⁻⁵𝑒𝑉 with mixing angles. When L/E=0.1, the nature of neutrino oscillation probability is analysis at four angles 50, 100, 150, and 200. In L/E=0.1 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0 to 0.7×10^-7, 0.1 to 2.1×10^-7, 0.1 to 2.5×10^-7), and 0.05 to 0.9×10^-7, respectively at the same mixing angle of 45 degrees. After that the neutrino oscillation probability decreases up to 0.4×10^-7, 1.2×10^-7, 1.4×107, and 0.8×10^-7, at the mixing angle of 580.

For L/E=0.2 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0 to 1.2×10^-7, 0.2 to 4.1×10^-7, and 0.2 to 4.9×10^-7, 0.1 to 2.8×10^-7 respectively at the same mixing angle of 45 degrees. After that, the neutrino oscillation probability decreases up to 1.1×10^-7, 3.5×10^-7, 4×107, and 2.3×10^-7 at the mixing angle of 580. For L/E=0.3 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0 to 2×10^-7, 0.4 to 6×10^-7, 0.4 to 7.4×10^-7, and 0.2 to 4×10^-7 respectively at the same mixing angle of 450. After that, the neutrino oscillation probability decreases up to 1.9×10^-7, 5.2×10^-7, 6.1×10^-7, and 3.4×10^-7 at the mixing angle of 580. For L/E=0.4 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0.02 to 0.3×10^-6, 0.06 to 8.2×10^-6, 0.06 to 9.9×10^-6, and 0.04 to 0.55×10^-6 respectively at the same mixing angle of 450. After that the neutrino oscillation probability decreases up to 0.24×10^-6, , 8×10^-6 , and 2.3×10^-6 at the mixing angle of 580.

For L/E=0.5 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0.02 to 0.35×10^-6, 0.06 to 1.15×10^-6, 0.06 to 1.25×10^-6, and 0.04 to 0.7×10^-6 respectively at the same mixing angle of 45 degrees. After that the neutrino oscillation probability decreases up to 0.3×10^-6, 0.88×10^-6, 1×10^-6, and 0.58×10^-6 at the mixing angle of 580. For L/E=0.6 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0 to 0.4×10^-6, 0.1 to 1.25×10^-6, 0.1 to 1.45×106, and 0.05 to 0.85×10^-6 respectively at the same mixing angle of 45 degrees. After that the neutrino oscillation probability decreases up to 0.35×10^-6, 1.05×10^-6, and 1.2×10^-6, and 0.7×10^-6 at the mixing angle of 580.

For L/E=0.7 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0 to 0.5×10^-6, 0.1 to 1.4×10^-6, and 0.1 to 1.75×10^-6, and 0.05 to 0.9×10^-6 respectively at the same mixing angle of 45 degrees. After that the neutrino oscillation probability decreases up to 0.4×10^-6, 1.2×10^-6, 1.4×106, and 0.8×10^-6 at the mixing angle of 580. For L/E=0.8 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0 to 0.55×10^-6, 0.1 to 1.7×10^-6, and 0.1 to 1.9×10^-6, and 0.05 to 1.1×10^-6 respectively at the same mixing angle of 45 degrees. After that the neutrino oscillation probability decreases up to 0.5×10^-6, 1.4×10^-6, 1.6×10^-6, and 0.9×10^-6 at the mixing angle of 58. For L/E=0.9 condition, the probability of neutrino oscillation gradually increases with increasing the mixing angle in all four constant angles 50, 100, 150, and 200 from 0 to 0.7×10^-6, 0.1 to 1.85×10^-6, 0.1 to 2.25×10^-6, and 0.05 to 1.3×10^-6 respectively at the same mixing angle of 45 degrees. After that the neutrino oscillation probability decreases up to 0.6×10^-6, 1.6×10^-6, and 1.8×10^-6, and 1.05×10^-6 at the mixing angle of 580.

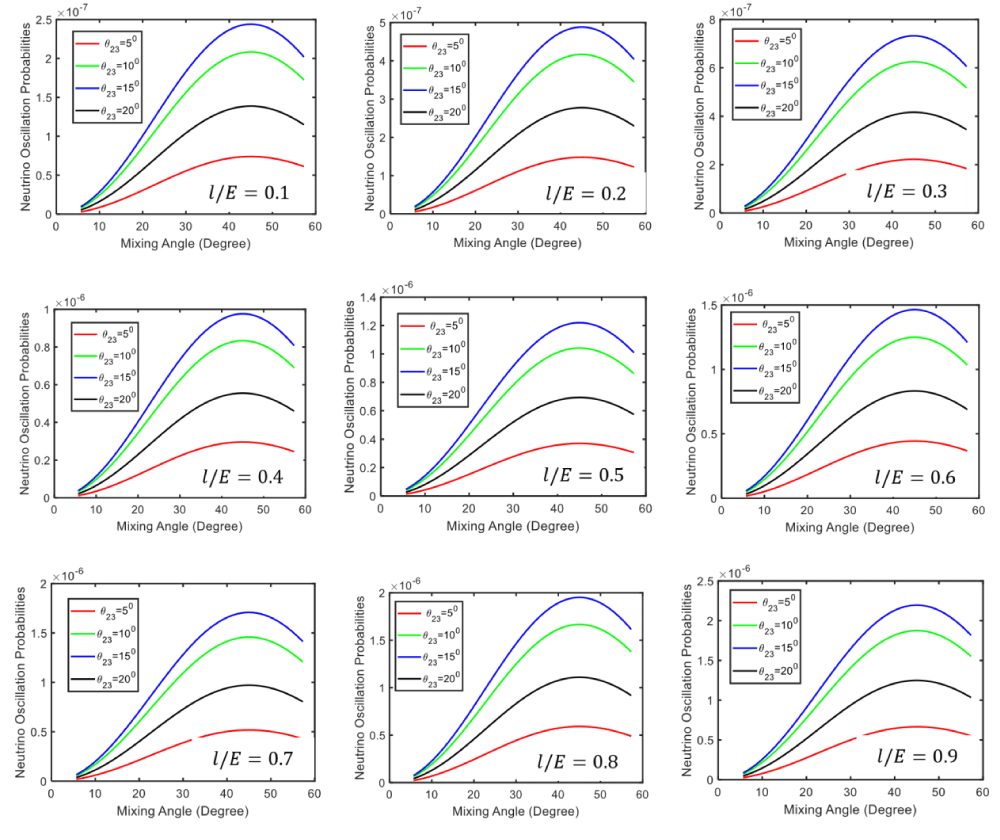
The numerical analysis of equation (26) is based on Δ𝑚² = 10⁻⁵𝑒𝑉 with consider 𝜃₂₃ and L/E=0.1 to 0.9 the nature us show in Figure 3. In the Figure 3, we clearly see the nature of the neutrino oscillation probability based on Δ𝑚² = 10⁻⁵𝑒𝑉 with mixing angles. When L/E=0.1, the nature of neutrino oscillation probability is analysis at four angles 50, 100, 150, and 200. In L/E=0.1 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 0.7×10^-7 to 0, 1.9×10^-7 to 0, 2.35×10^-7 to 0, and 1.3×10^-7 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again start to increase at mixing angle of 500.

For L/E=0.2 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 1.4×10^-7 to 0, 3.9×10^-7 to 0, 4.6×10^-7 to 0, and 2.6×10^-7 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again start to increase at mixing angle of 500. For L/E=0.3 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 2 ×10^-7 to 0, 5.8×10^-7 to 0, 6.8×10^-7 to 0, and 3.9×10^-7 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again starts to increase at mixing angle of 500.

For L/E=0.4 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 0.25×10^-6 to 0, 0.78×10^-6 to 0, 0.9×10^-6 to 0, and 0.5×10^-6 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again starts to increase at mixing angle of 500. For L/E=0.5 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 0.36×10^-6 to 0, 0.88×10^-6 to 0, 1.16×10^-6 to 0, and 0.66×10^-6 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again starts to increase at mixing angle of 500. For L/E=0.6 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 0.4×10^-6 to 0, 1.16×10^-6 to 0, 1.38×10^-6 to 0, and 0.78×10^-6 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again starts to increase at mixing angle of 500.

For L/E=0.7 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 0.49×10^-6 to 0, 1.35×10^-6 to 0, 1.6×10^-6 to 0, and 0.8×10^-6 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again starts to increase at mixing angle of 500. For L/E=0.8 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 0.52×10^-6 to 0, 1.5×10^-6 to 0, and 1.8×10^-6 to 0, and 1××10^-6 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again starts to increase at mixing angle of 500. For L/E=0.9 condition, the probability of neutrino oscillation gradually decreases with increasing the mixing angle in all four angles 50, 100, 150, and 200 from to 0.6 ×10^-6 to 0, 1.75×10^-6 to 0, 2×10^-6 to 0, and 1.2×10^-6 to 0 respectively at the same mixing angle of 40 degrees. After some constant zero probability, the neutrino oscillation probability again starts to increase at a mixing angle of 500.

The numerical analysis of developed equation (27) is based on Δ𝑚² = 10⁻⁵𝑒𝑉 wth consider and L/E=0.1 to 0.9 and the nature is shows in Figure’s 4. The figure 4 shows the same nature of probability of oscillation of neutrino in four different angle 50, 100, 150, and 200 in all the condition of L/E=0.1 to 0.9 based on Δ𝑚² = 10⁻⁵𝑒𝑉 with mixing angles. The neutrino oscillation probability gradually decreases with increasing the mixing angles in degree. The neutrino oscillation probability becomes maximum at the mixing angle of 45 degree. Finding the minimum probability certainly change the probability by increasing its value. The maximum probability of neutrino oscillation is at a mixing angle of 5 degrees

We analyze the probability of neutrino oscillation when the four flavor of neutrino mixed. First of all, we observed the nature of two flavor neutrino oscillation based on the equation (19) and (20) only one condition of Δ = 0.1 . In this observation we found that the neutrino oscillation probability decreases with increasing the mixing angles in equation (19) but in equation (20) we found reverse probability, increases with increasing the mixing angle. After that we analyze the three-flavor neutrino oscillation based on the Δ𝑚2 = 10−5𝑒𝑉 and L/E=0.1 to 0.9 condition respectively in the four different angles 50, 100, 150, and 200. By observation based on the equation (25) and the neutrino oscillation probability from ve → vµ, the neutrino oscillation probability increases with increasing the mixing angles. In all the condition, the maximum probability is shown at the mixing angle of 45 degree in the angle of 15 degree and minimum probability of oscillation in angle of 5 degree. According to the equation (26), the oscillation probability of neutrino decreases with increasing the mixing angles when ve → vτ. The neutrino oscillation probability is maximum in the initial mixing angles after that the probability becomes zero. The maximum probability is seen in the angle of 150 by comparing all the four angles followed by all the conditions. Followed by equation (27), we also find the same nature but in different character. The neutrino oscillation decreases with increase in mixing angles. But in this case, the maximum neutrino probability given by an angle of 5 degree instead of the angle of 15 degrees.

Authors would like to thanks all faculties members of department of Physics, Patan Multiple Campus, PatanDhoka, Tribhuvan University, Lalitpur Nepal. In addition, Authors would also like to thanks all team members of Innovative Ghar Nepal and Robotics Academy of Nepal, Lalitpur for proving research environment and space during this research work.

1. Kruppke D. On Theories of Neutrino Oscillations. Diploma Thesis. 2007.
2. Kopp J. Phenomenology of Three-Flavour Neutrino Oscillations. Physik-Department. Technische Universitat Munchen.2006.
3. Gonzalez-Garcia MC, Yokoyama M. Neutrino Masses, Mixing, and Oscillations. Physical Review D. 2018; 98:6-9.
4. Nunokawa H. Neutrino Mass, Mixing and Oscillations. Brazilian Journal of Physics. 2000; 30(2):346-356.
5. Upadhyay A, Batra M. Phenomenology of Neutrino Mixing in Vacuum and Matter. ISRN High Energy Physics. 2013.
6. Thomson M. Handout 11: Neutrino Oscillations. Lecture Note.2011.