The Second Law of Thermodynamics in Irreversible Isothermal Processes (Dedicated to the 200^th anniversary of thermodynamics)

Isothermal irreversible processes under electromagnetic radiation are considered by the “black box” method. The laws of efficiency of conversion of electromagnetic radiation energy into Helmholtz free energy are obtained. The origin of the «white spots» of modern knowledge in various fields of science is explained, which ensures their elimination.

Preface

Thermodynamics emerged in the 19^th century as a response of physicists to the problems of English engineers who created a steam engine. In the 20^th century, quantum thermodynamics emerged as a result of the activities of physicists who solved the problem of creating effective light sources based on luminescence processes. The foundation of quantum thermodynamics was laid by the works of Wilhelm Wien [1], Max Planck [2], Albert Einstein [3], Lev Landau [4], M. A. Weinstein [5], Peter Landsberg [6,7], and Yulia Chukova [8,9]. Luminescence can be of different types depending on the nature of the exciting agent. When considering limiting the efficiency of chemiluminescence, the problem of the efficiency of converting electromagnetic radiation into Helmholtz free energy was solved along the way [10]. Such energy conversion takes place in solar panels.

Open systems

Conversion of electromagnetic radiation into Helmholtz free energy in one form or another exists in all processes, but it is especially familiar and experimentally studied for processes in living systems under short-wave solar radiation (the Wien radiation), which A. Einstein called the Wien radiation. Living systems within the framework of thermodynamic terminology are open systems that exchange energy (electromagnetic radiation and heat) and mass (energy of the flow of reagents and energy of the flow of products) with the environment. In thermodynamic consideration, it is not the entire flux of incident electromagnetic radiation that is important, but only ${\dot{W}}_a$ , its absorbed part, which we denote $\dot{\dot{Q}}.$ . The energy flows of reagents and products are denoted by ${\dot{U}}_r$ and ${\dot{U}}_p$ , respectively. Thermodynamic consideration requires the mandatory introduction of the entropy of all the energies under consideration, which we denote ${\dot{S}}_a$ , ${\dot{S}}_r$ , and ${\dot{S}}_p$ . For heat flux, we use the Clausius formula $\dot{\dot{Q}}/T$ , where T is the system temperature. Based on the law of conservation of energy, we have:

${\dot{W}}_a+{\dot{U}}_r+{\dot{U}}_p-\dot{\dot{Q}}=0$ (1)

Let us limit the consideration to the stationary state of the system, then we have for the balance of entropy flows

${\dot{S}}_a+{\dot{S}}_r-{\dot{S}}_p-\dot{\dot{Q}}/T+{\dot{S}}_i=0$ (2)

For efficiency η of conversion of electromagnetic energy into the Helmholtz free energy F, we have:

η = ΔF/ΔWa (3)

As the Helmholtz free energy F is determined by the formula F = U – ST, where U is the internal energy of the system and ST is a bound energy. The bound energy cannot be converted into work, so the Helmholtz free energy is less internal energy by the value of the bound energy. In our notation, efficiency η is entered by the formula

$\eta =[({\dot{U}}_p-{\dot{S}}_{p}T)-({\dot{U}}_r-{\dot{S}}_{r}T)]/{\dot{W}}_a$ (4)

Taking into account equations (1) and (2), we have for η

$\eta =1-T({\dot{S}}_a+{\dot{S}}_i)/{\dot{W}}_a$ (5)

All calculations in thermodynamics begin with the calculation of the thermodynamic limit *, i.e., with the consideration of reversible processes, which do not exist in nature. This is one of the reasons why experimenters dislike thermodynamics.

In reversible processes, the entropy generation rate ${\dot{S}}_i$ ‘i’ is zero, and formula (5) takes the form similar to Carnot’s formula

${\eta }^{*}=1-T{\dot{S}}_a/{\dot{W}}_a$ (6)

The absorbed power ${\dot{W}}_a$ is determined by formula ${\dot{W}}_a={\displaystyle \int E_v}{d}_v$ , where ‘Ev’ is the spectral density of absorbed radiation at frequency ‘ν’, and the entropy flux of absorbed radiation is determined by the formula (7) proposed by Landau in 1946 based on the formula previously derived by Planck for equilibrium radiation [2].

${\dot{S}}_a=2\Pi kc-2{\displaystyle \int v2[(1+\rho )ln(1+\rho )}-\rho ln\rho ]dv$ (7)

Where ‘ρ’ is a characteristic function, defining the degree of filling of electronic levels. Unlike Planck, Landau offered to count S for nonequilibrium radiation according to the Landau formula

$\rho =c2Ev/2\Pi hv3$ (8)

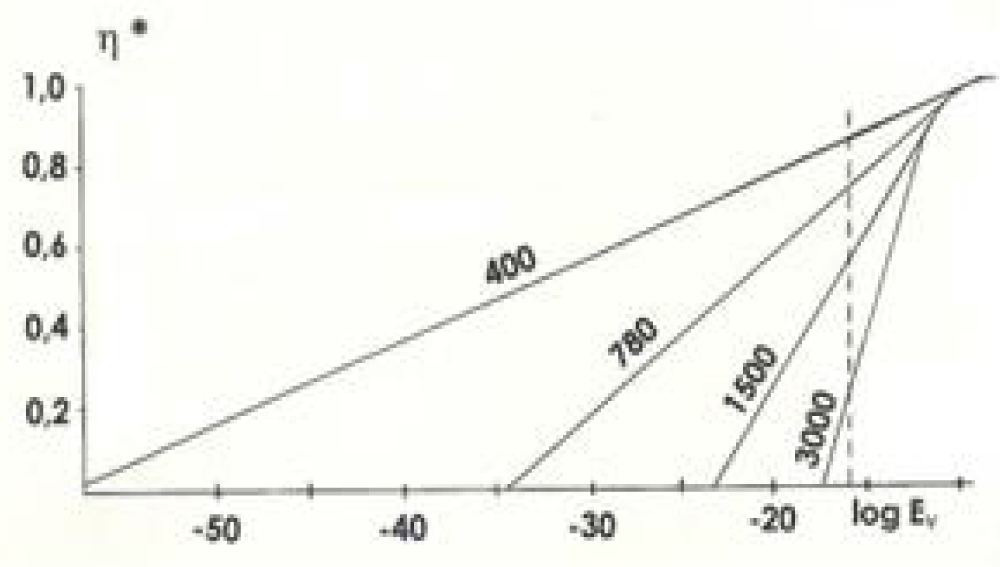
Where ‘к’ is the Boltzmann constant, ‘h’ is the Planck constant, and ‘с’ is the light velocity. The legality of such a definition was confirmed by works [11,12]. The abundance of experimental results in all sections of photobiology (human vision, photosynthesis of plants and algae, photomovement of protozoa, and others) made it possible to explain by thermodynamic method not only those results that scientists easily explained using molecular kinetic methods, but also those that for a hundred years remained in the status of not fully understood, although between them famous scientists such as S.I. Vavilov, F. Perren and others worked. The result of the calculation η* for several frequencies (wavelengths 400 -780 nm are visible light, 1500 nm and 3000 nm are infrared radiation) of absorbed radiation is given in 10^-19 on a semi-logarithmic scale. The rectilinear section testifies that the dependence of limiting efficiency η* on absorbed power is logarithmic.

The vertical dotted line in Figure 1 marks the maximum spectral density of solar radiation Eν that can be recorded at the Earth’s surface. The right (from the dotted line) part of Figure 1 has nothing to do with the processes taking place on Earth. All processes, which are interesting for the restrictions, are depicted in the left part (Eν is measured in J/cm²).

Elimination of white spots

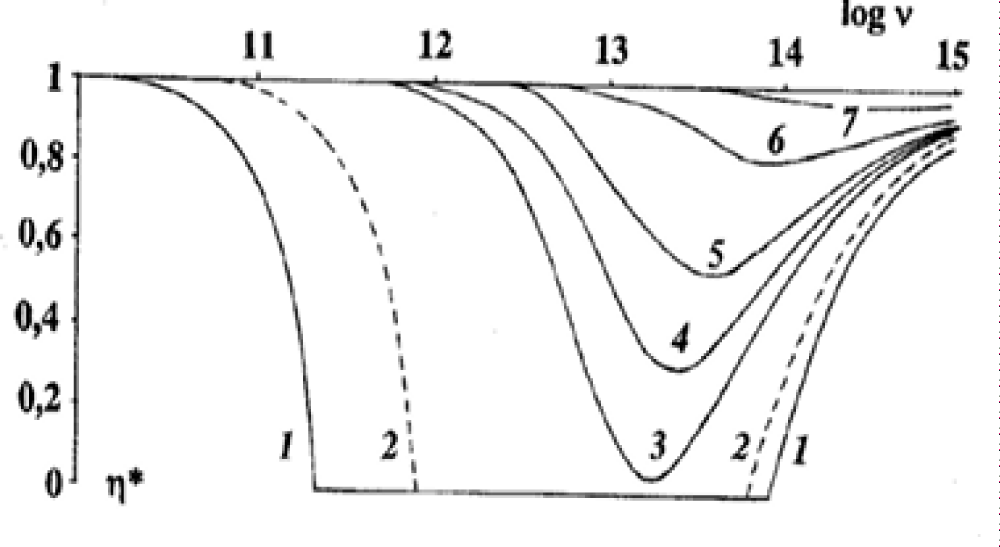
As is known, experiments are used to verify the correctness of the theory. Let us start from the human vision, which is not only comprehensively studied but also standardized by relevant international organizations. And, nevertheless, for more than a hundred years, there has been no answer to the question of why the eye has zero sensitivity in the area where the maximum of solar radiation is. Thermodynamics gives an exhaustive answer to it (Figure 2).

Figure 2 shows the frequency dependence of the limiting efficiency η* in the frequency range from 1010 Hz to 1015 Hz (visible and IR radiation range) for 7 values of the spectral density of absorbed radiation. The spectral density of the absorbed radiation E changes from 10^-19 J/cm² (curve 1) to 8.10-6 (curve 7). Among them, the most important for us is the dotted line 2, which corresponds to the maximum spectral density of solar radiation at the Earth’s surface.

Curve 2 in Figure 2 demonstrates a complete prohibition on the conversion of IR (infrared) radiation into Helmholtz free energy. The prohibition weakens in the high-frequency region (the Wien region) and the low-frequency region (the Rayleigh-Jeans region). Among curves 3-7, the spectral density of electromagnetic radiation increases with the number by three orders of magnitude (a thousand times). Curve 1 refers to the normal lighting conditions on Earth. With the change of illumination from day to night, the spectral density of radiation drops by 20-30 orders of magnitude, and the prohibition on the conversion of IR radiation becomes even tougher. Einstein called high-frequency radiation the Wien radiation [3]. In the Wien region, the dependence η* on the spectral density of radiation Ev on a semi logarithmic scale has the form of a straight line with a different slope for different wavelengths, which is shown in Figure 1. This means that the dependence η* on the spectral density of the absorbed radiation Ev is logarithmic as Fechner claimed [13]. In the study of human vision, there was a tragic story that is waiting for its Shakespeare, and now I will just remind the exact dates of the beginning and end of this tragedy. In 1860, the book [13] was published by G.T. Fechner’s “Elements of Psychophysics”, in which the dependence of a person’s sensation on the magnitude of the influencing stimulus is given. The first stimulus studied was a burning candle. The dependence turned out to be logarithmic. The rest of the senses obeyed the same law, which became known as the Weber-Fechner law. Weber was an experimenter who conducted experiments, and Fechner was a theorist who integrated the ratio obtained by Weber. The Weber-Fechner law was the basic law of psychophysics and one of the basic laws of general sensory physiology. It lasted for a long time, and in 1960, at the celebration of its centenary, it was canceled by S.S. Stevens, and this cancellation was formally consolidated in 1961 by the publication of his paper entitled “To honor Fechner and repeal his law” with the subtitle “A power function, not a log function, describes the operating characteristic of a sensory system” [14].

But by 2010, I had shown [15] that the Weber-Fechner law is a special case of the general thermodynamic law of converting electromagnetic radiation into Helmholtz free energy, and as one of the basic laws of nature, cannot be canceled by a scientist, a journal, or even the most powerful ruler. In 2010 [16], at the Lomonosov Moscow State University, at the seminar on synergetics, a presentation of the book by Yu. Chukova’s “Weber Fechner Law” to the 150^th anniversary of the publication of the book “Elemente der Psychophysik” by G.T. Fechner. Representatives of the German Embassy in Moscow were invited to the presentation.

The next “why?” was associated with the Purkyne effect, which was discovered by the Czech physiologist Jan Purkyne. The effect is extremely simple: red objects seem brighter during the day, and blue ones in the evening. Why? The answer seems to have been found when it turned out that there are two types of light receptors in the retina of the human eye: cones and rods. Cones work in daylight, and rods at night. But why did the eye create two types of receptors? It is the question that physiology has not been able to answer for more than a hundred years.

Thermodynamics (Figure 1) gives a simple answer to it. The maximum sensitivity of cones and rods is shifted by 50 nm. This is a lot when compared with the total length of the visible light range (about 400 nm). The eye works during the transition from day to night in the range of more than 20 orders of illumination. During the day, cones work in bright light, but as the illumination decreases, their efficiency decreases, and sensitivity remains only in the blue part where the cones work. The term “Purkyne effect” is used only when considering the work of the human eye, but in reality, it is an effect that can be observed in a wider class of light converters, which we will return to below. It is useful to emphasize here that in the sciences that study human vision (physics, physiology, medicine), the concept of efficiency is not used at all, but the power of the laws of nature is so great that they manifest themselves regardless of whether Homo sapiens has already managed to study and formulate them, or does not consider it necessary to do so. Thermodynamics was able to eliminate the three largest white spots in the sciences of human vision at the level of consideration in the thermodynamic efficiency limit, which experimenters treat almost contemptuously.

Consideration of irreversibility

For the result to be of interest to experimenters, it is necessary to calculate according to formula (5), taking into account the irreversibility Si of real processes. The Brussels School of Thermodynamics has been dealing with this problem for several decades. As you know, one of the formulations of the second law of thermodynamics is the statement that entropy increases. The founder of the Brussels School of thermodynamics, Theophil De Donde, introduced the concept of entropy generation rate, which was studied by his student Ilya Prigogine [17], who was awarded the Nobel Prize in chemistry in 1977. As shown by the Nobel Prize winner in chemistry, Onzager (1968), with a weak effect on the system, irreversibility increases in proportion to the influencing factor [18]. With a strong influence of the superlinear [15,16,19-22].

Ṡi = αẆa + βẆna- (9)

Where α and β are constants and n > 1.

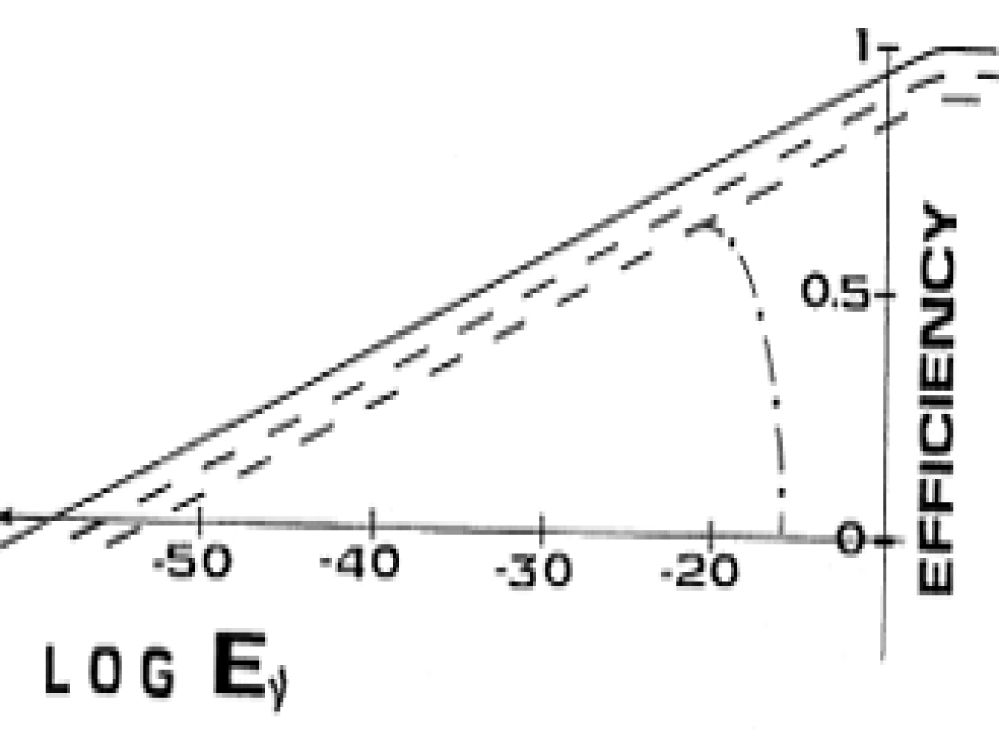
The effect of irreversibility on efficiency is shown in Figure 3, in which the limit efficiency is represented by a solid line, the two dotted lines are the real efficiency under the conditions of the linearity of the process. For the lower line, Si is greater than for the first case.

The area of linear growth of the entropy generation rate is limited from above. When the growth becomes supper linear, the efficiency η passes through the maximum and shows a decline (dot-and-dash line in Figure 3). Thus, the experimenter will see a complex curve consisting of a logarithmic component (dotted line) at the beginning of the process, a maximum and subsequent sharp decline (dot-and-dash line). Such a curve will be seen by a good experimenter, whose laboratory devices work in a wide range of Ev changes [15,16].

Photosynthesis

Photosynthesis of algae and plants (the breadwinner of all life on the planet) is the only field of living systems sciences where the concept of efficiency is used. This efficiency is small. To increase it, such research has been well funded in many countries for many decades. Their result is not comforting: “The maximum yield of rice has not changed in 30 years. We have reached a plateau in the production of biomass, and there is no simple explanation for this.” This is a quote from a scientific monograph [23]. Specialists in plant photosynthesis considered thermodynamics not applicable to this complex object of research. Meanwhile, thermodynamics easily explains their disappointing result. But this can no longer be done without taking into account irreversibility. In addition, it is necessary to introduce the concepts of endergonic and exergonic processes. Endergonic processes are processes that go with an increase in Helmholtz free energy, and exoergic processes go with its decrease.

As can be seen from Figure 3, any smallest irreversibility reduces the absolute value of efficiency and shifts the beginning of the endergonic process towards higher values of Ev. In the science of photosynthesis, the starting point of the endergonic process is called the compensation point. On one side of it lies the sphere of exergonic processes, and on the other endergonic (photosynthesis). This point is well known to experimenters, and its position on the axis of external influence is sometimes measured in absolute units. This made it possible to assert that on the line of the thermodynamic limit of efficiency η*, the compensation point of unicellular algae lies at a value of η* = 70%, for shade-loving plants at the compensation point η* = 73.5%, and for light-loving plants η* = 76%. Since in terrestrial conditions the maximum value of the thermodynamic limit of photosynthesis efficiency is 81.5%, a very narrow band of creatures remain for the universal breadwinner: 5.5% for light-loving plants, 8% for shade-loving plants, and 11.5% for unicellular algae. And these values should be considered overpriced due to the initial conditions of the estimated calculation [22]. For billions of years of its existence, nature has moved so close to the thermodynamic limit that modern scientists cannot improve the efficiency of photosynthesis, despite all their efforts. Researchers of photosynthesis do not understand that they are trying to overcome the thermodynamic limit of efficiency.

Photomovement of the simplest living organisms

The third area, well-studied experimentally to date, is the photomovement of the simplest organisms (euglena, chlamydomonas, cyanobacteria, etc.) [24,25]. These tiny living creatures (a few microns in size) are so simple in structure that sometimes they do not even have a nucleus in the cell. But by studying their behavior, you can see not only the thermodynamic patterns described above, but also many others, which we will not mention in this paper. Photomovement can be of different types (phototaxis, photokinesis, and phobotaxis). Phototaxis is the name of the movement of protozoa towards the light source (positive phototaxis) or away from it (negative phototaxis). Visually, the phenomenon looks like this: when a light source appears, the organism (for example, Euglena) begins to move towards it, but as it approaches, the movement slows down, at some point, the Euglena stops, and then begins to move away from the light source. Biologists (as best they could) explained the positive phototaxis and even established that it obeys the Weber-Fechner law [26], but there were not even hypotheses to explain everything else.

Figure 4 shows the place of different processes on the efficiency curve. The human vision is given by the dotted line, the photosynthesis is given by the dot-and-dash line. The solid line is a theoretical calculation [20,27]. The dots are experimental results for solar panels with energy concentration. And the photomovement of protozoa can be in any part of a solid line.

Solar panels and the boundary (Limits) of applicability of the theory

A quantitative verification of the correctness of the thermodynamic theory was carried out on solar panels [20,27]. Solar panels helped to understand the physical meaning of such curves with maximum. In the entire range of ordinary solar radiation, solar panels demonstrate a logarithmic increase of efficiency (Weber-Fechner law). But, when the experimenters began to use solar radiation concentrators, which made it possible to increase the impact by 500 and even 1000 times, the efficiency showed a maximum and a subsequent decline. What is the physical meaning of the curve with the maximum in Figure 3? As long as the entropy generation rate increases in proportion to energy absorption, the ratio of the energy fractions converted into free energy and thermal energy remains constant. Under strong influence, the entropy generation rate begins to grow superlinearly, and the fraction of the absorbed energy converted into heat begins to grow faster than the fraction converted into Helmholtz free energy. As a result, the system begins to heat up, and the efficiency decreases. Living systems are very sensitive to temperature changes (for humans, the entire width of such a range is 10 degrees Celsius). An increase in temperature reduces the comfort of life. And to regain the lost comfort, Euglena begins to move away from the source and thereby returns the necessary comfort.

Solar panels devoid of behavioral response are destroyed. The most complex photoresponses were observed by the German biologist Wilhelm Nultsch [28-30], whose equipment allowed the experiment to be carried out in the widest range of changes in the spectral density of radiation Ev (or illumination). No one could explain them, and therefore no one referred to them. And it took me a lot of work to find them [22].

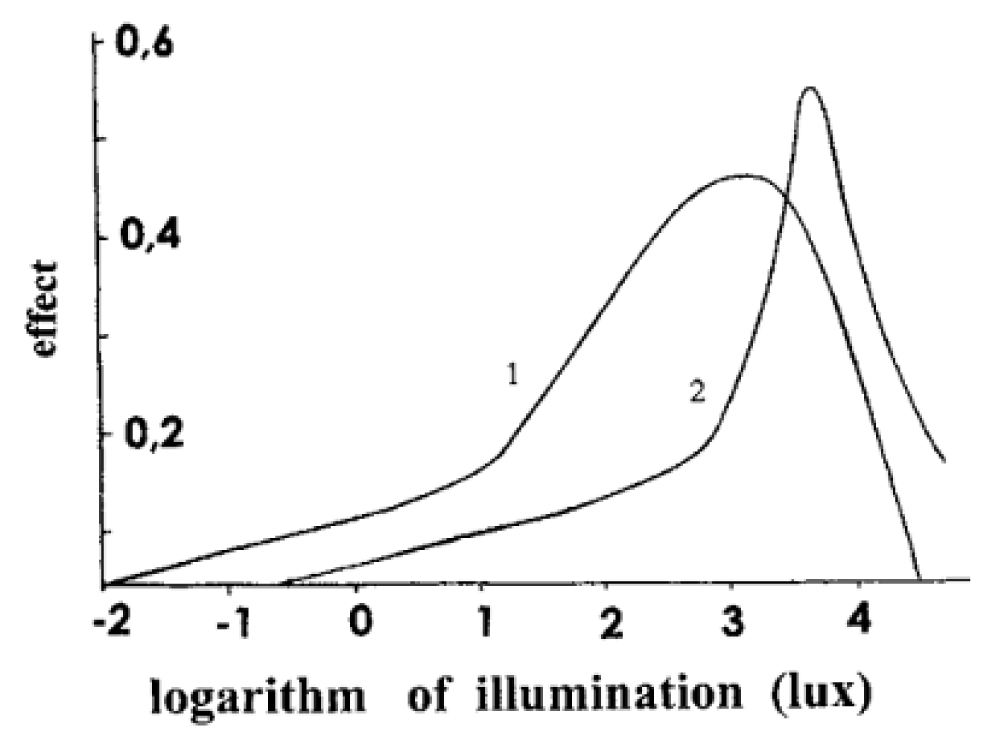
Thermodynamics provides a simple explanation, directly predicts such a complex curve in systems with two well-separated absorption spectra. Two rectilinear sections of curve 2 (Figure 5) are the Purkyne effect. When the absorption bands expand (curve 1 in Figure 5) and even more so when they merge, striking distinctness is lost gradually, and as a result, it will become difficult to fix as in a human eye. In photobiology, there are other less well-known, but well-studied effects with their white spots, which thermodynamics successfully explains [22].

The above contains a step forward. It is related to the entropy generation rate (9). According to the second law of thermodynamics, entropy increases. But the question was open as to what law is the increase. Taking into account Onsager’s achievements, which were awarded the Nobel Prize in chemistry just at the time when I had an interest in the thermodynamics of luminescence, I assumed that with weak effects on the system and weak luminescence, the entropy generation rate can increase linearly with increasing exposure. This assumption was confirmed [22].

When considering endergonic processes in conditions of weak impact on the system, the situation is similar, and in conditions of strong impact, the increase is superlinear, which determines the decline in efficiency. Here it is appropriate to recall the words of Max Planck: “This is a step of fundamental importance, the validity of which can be proved only by checking the consequences arising from it”. All of the above demonstrate the step itself of fundamental importance and correctness of the conclusions that follow from it. The limited volume of this paper did not allow for to inclusion of consideration of the effects of long-wave radiation, which also confirms the correctness of the step taken [31-33].

The above method works at the population level, if we are talking about the simplest organisms, which have predetermined the zonality of algae in the ocean. At a depth of 10 meters, green algae live, brown algae are located under them to a depth of 25 meters, and even lower to a depth of 100 meters, and red algae live [33]. But when I discovered the experiments [34], it became clear that their experimental level was far from what physics required. And here I came across the first report of the Club of Rome and its later versions. The applicability of my method to these systems requires additional consideration. But already now we can say something about the broad generality of the laws obtained [35].

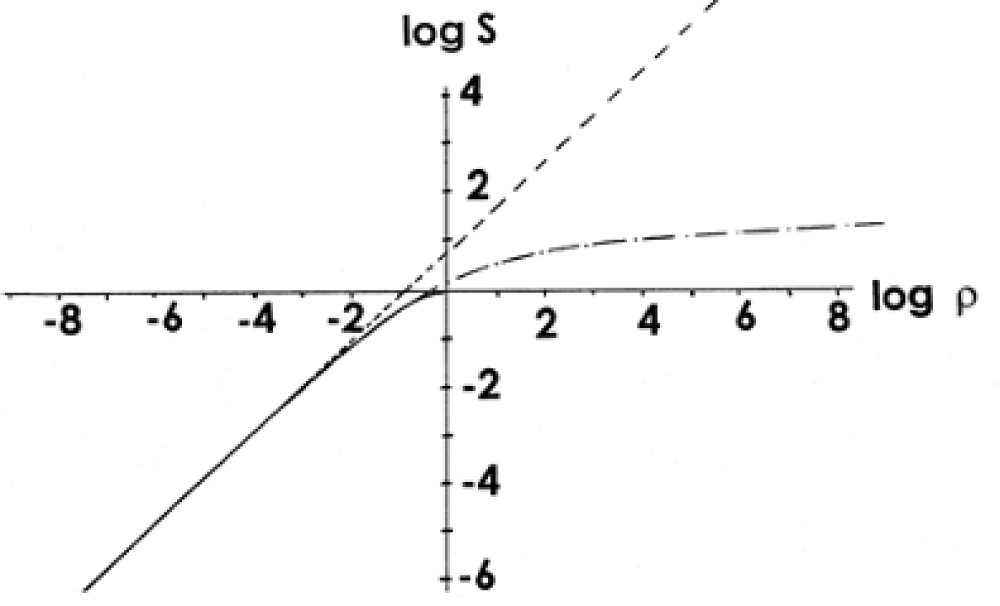
In Figure 6, the logarithm ρ is postponed along the abscissa axis, and the logarithm of entropy for ensembles of particles with integer spin (bosons, solid line and dot-dash line) and classical particles (solid line and dotted line) is postponed along the ordinate axis. There is also a third line for an ensemble of particles with half-integer spin (fermions, solid line).

All the results discussed above in this paper relate, to small ρ (lower left quadrant), which indicates a very wide scope of their applicability, much wider than those specific examples (vision, photosynthesis and photomovement) discussed above, and they are enough to understand how to avoid that final catastrophe, which was announced to the world by Meadows [35].

1. Wien W. Temperature and entropy of radiation. Ann Phys (Berl). 1894;288(5):132-165. Available from: https://doi.org/10.1002/andp.18942880511
2. Planck M. The theory of heat radiation. Philadelphia: Blakiston; 1914. Available from: https://gutenberg.org/files/40030/40030-pdf.pdf
3. Einstein A. On a heuristic point of view concerning the production and transformation of light. Ann Phys (Berl). 1905;322:132-148. Available from: https://doi.org/10.1002/andp.19053220607
4. Landau L. On the thermodynamics of photoluminescence. J Phys USSR. 1946;10:503.
5. Weinstein MA. Thermodynamic limitation on the conversion of heat into light. J Opt Soc Am. 1960;50(6):597-602. Available from: https://doi.org/10.1364/JOSA.50.000597
6. Landsberg PT, Evans DA. Thermodynamic limits for some light-producing devices. Phys Rev. 1968;166(2):242. Available from: https://doi.org/10.1103/PhysRev.166.242
7. Landsberg PT, Tonge G. Thermodynamic energy conversion efficiencies. J Appl Phys. 1980;51(7):R1-R20. Available from: https://doi.org/10.1063/1.328187
8. Chukova YuP. Thermodynamic limit of the luminescence efficiency. Lett J Tech Phys. 1969;10:458-460.
9. Chukova YP. The region of thermodynamic admissibility of light efficiencies larger than unity. Zh Eksp Teor Fiz. 1975;68:1234-1240. Available from: http://www.jetp.ras.ru/cgi-bin/dn/e_041_04_0613.pdf
10. Chukova YuP. On the ultimate efficiency of converting light energy into chemical energy. High Energy Chem. 1977;11(2):126-130.
11. Rosen P. Entropy of radiation. Phys Rev. 1954;96(3):555. Available from: https://doi.org/10.1103/PhysRev.96.555
12. Ore A. Entropy of radiation. Phys Rev. 1955;98(4):887. Available from: https://doi.org/10.1103/PhysRev.98.887
13. Fechner GT. Elements of psychophysics. Vol. 2. Leipzig: Breitkopf und Härtel; 1860. Available from: https://archive.org/details/elementederpsych001fech/page/n7/mode/2up
14. Stevens SS. To honor Fechner and repeal his law: A power function, not a log function, describes the operating characteristic of a sensory system. Science. 1961;133(3446):80-86. Available from: https://doi.org/10.1126/science.133.3446.80
15. Chukova YuP. On the spectral sensitivity of the human eye. Dokl Akad Nauk SSSR. 1988;300(2):504-507.
16. Chukova YP. The Weber-Fechner law. To the 150^th anniversary of the publication of the book "Elemente der Psychophysik” by G.T. Fechner. Moscow; 2010.
17. Prigogine I. Time, irreversibility and structure. In: Mehra J, editor. The physicist’s conception of nature. Dordrecht: Springer Netherlands; 1973. p. 561-593. Available from: https://philpapers.org/rec/PRITIA-4
18. Onsager L. Reciprocal relations in irreversible processes. I. Phys Rev. 1931;37(4):405. Available from: https://doi.org/10.1103/PhysRev.37.405
19. Chukova YuP. Features of the bioresponse under the influence of electromagnetic radiation of the radio range. Dokl Akad Nauk SSSR. 1990;311(2):506-508.
20. Chukova YuP. Unexpected relationship: Thermodynamic consideration of some photoprocesses. Moscow: Znanie; 1991. No. 4. (Physics Series).
21. Chukova YP. Advances in nonequilibrium thermodynamics of the systems under electromagnetic radiation. Moscow: Academy of Sciences; 2001.
22. Chukova YP. Introduction to quantum thermodynamics of irreversible isothermal processes. Moscow (Russia): Megapolis; 2018. Available from: https://market.yandex.ru/product--vvedenie-v-kvantovuiu-termodinamiku-neobratimykh-izotermicheskikh-protsessov/1781387083?sku=836840923&uniqueId=7450942&do-waremd5=p-C103xG_cupA5U1NfBKnQ
23. Gusev MV, Nikitina KA. Cyanobacteria: (Physiology and metabolism). Moscow: Science; 1979. Available from: https://rusneb.ru/catalog/002178_000020_BGUNB-BEL%7C%7C%7CBIBL%7C%7C%7C0000401778/
24. Wolken JJ. Photobiology. New York, London: Academic Press; 1968.
25. Wolken JJ. Euglena. New Brunswick: Rutgers University; 1961.
26. Diehn B, Tollin G. Phototaxis in Euglena—II. Physical factors determining the rate of phototactic response. Photochem Photobiol. 1966;5(7):523-532. Available from: https://doi.org/10.1111/j.1751-1097.1966.tb09842.x
27. Rzhanov AV, Chukova YP. Limiting energy characteristics of direct conversion of solar radiation. Dokl Akad Nauk SSSR. 1984;276(6):1385-1388. Available from: https://www.osti.gov/etdeweb/biblio/6283863
28. Nultsch W. The influence of light on the movement of cyanophyceae: I. Report Photo Topo taxis of Phormidium autumnale. Planta. 1961;56:632-647. Available from: https://link.springer.com/article/10.1007/BF01928208
29. Nultsch W. The influence of light on the movement of cyanophyceae: Part II: Photokinesis in Phormidium autumnale. Planta. 1962;57:613-623. Available from: https://link.springer.com/article/10.1007/BF01930343
30. Nultsch W. The influence of light on the movement of cyanophyceae: Part III: Photophobotaxis of Phormidium uncinatum. Planta. 1962;58:647-663. Available from: https://link.springer.com/article/10.1007/BF01914754
31. Chukova YP. Bose condensation and non-thermal processes in living systems under millimeter (MM) radiation. Electromagn Biol Med. 2009;28(1):41-45. Available from: https://doi.org/10.1080/15368370802708355
32. Chukova YP. Reasons of poor replicability of nonthermal bioeffects by millimeter waves. Bioelectrochem Bioenerget. 1999;48(2):349-353. Available from: https://doi.org/10.1016/S0302-4598(99)00034-3
33. Chukova YP. Interactions of science, technology and medicine: Electromagnetic radiation during the twentieth century. In: A Bridge between Conceptual Frameworks: Sciences, Society and Technology Studies. Springer; 2015. p. 85-111. Available from: https://link.springer.com/chapter/10.1007/978-94-017-9645-3_6
34. Southwood TRE. Entomology and mankind: Insects over the ages have greatly affected man’s health and food supply and have played an important role as religious and cultural symbols. Am Sci. 1977;65(1):30-39. Available from: https://www.jstor.org/stable/27847640
35. Chukova YuP. Energy laws of the biosphere as a basis for predicting the fate of our civilization. Russ J Biol Phys Chem. 2021;6(1):26-34.