Alternative Proof of the Ribbonness on Classical Link

Alternative proof is given for an earlier presented result that if a link in 3-space bounds a compact oriented proper surface (without closed component) in the upper half 4-space, then the link bounds a ribbon surface in the upper half 4-space which is a boundary-relative renewal embedding of the original surface.

2020 Mathematics Subject Classification: Primary 57K45; Secondary 57K40

For a set A in the 3-space R³ = {(x, y, z)|−∞ < x, y, z < +∞} and an interval

J ⊂ R, let

AJ = {(x, y, z, t)|(x, y, z) ∈ A, t ∈ J}.

The upper-half 4-space $R_{+}^4$ is denoted by R³[0,+∞). Let k be a link in the 3- space R³, which always bounds a compact oriented proper surface F embedded smoothly in the upper-half 4-space $k_0^{\text{'}}$ , where R³[0] is canonically identified with R³. Two such surfaces F and F′ in $R_{+}^4$ are equivalent if there is an orientation-preserving diffeomorphism f of $R_{+}^4$ sending F to F′, where f is called an equivalence. For a link k₀ in R³, let b be a band system spanning k₀, namely a system of finitely many disjoint oriented bands spanning the link k₀ in R³. The pair (k₀, b) is called a banded link. The surgery link of (k₀, b) is the link obtained from k₀ by surgery along b. Assume that the surgery link of a banded link (k₀, b) is a trivial link κ in R³. Then the band system b is considered as a band system β spanning κ. The pair (κ, β) is called a banded loop system with loop system κ and surgery link k₀. Throughout the paper, the surgery link k₀ will be a union k ∪ o of a link k in question and a trivial link o called an extra trivial link. Here, it is assumed that there is a band sub-system b₁ of the band system b such that b₁ connects to o with just one band b₁ ∈ b₁ for every component o ∈ o and every band spans the link k. Let α₁ be the arc system of the attaching arc α₁ of every band b₁ ∈ b₁ to o ∈ o, and ${\alpha }_1^c$ the complementary arc system of α₁ in o consisting of every complementary arc ${\alpha }_1^c=cl(0\backslash {\alpha }_1)$ . Any disk system d in R³ bounded by the extra trivial link o is called an extra disk system, which is fixed and the argument proceeds. Let δ be a disk system consisting of disjoint disks in R³ with ∂δ = κ, which is called a based disk system for a loop system κ. A ribbon surface-link cl( $F_{-1}^1$ ) in R⁴ is constructed from a banded loop system (κ, β) by taking the surgery of the trivial S²- link

O = ∂(δ[−1, 1]) = δ[−1] ∪ (∂δ)[−1, 1] ∪ δ [1]

along the 1-handle system β[−t, t] in R⁴ for any t with 0 < t < 1. The proper surface ucl $\left(F_0^1\right)=cl(F_{-1}^1)\cap R_{+}^4$ in $R_{+}^4$ is called the upper-closed realizing surface of a banded loop system (κ, β) with surgery link k₀. Note that choices of the based disk systems δ are independent of the equivalences of ucl( $F_0^1$ ) and cl( $F_{-\text{1}}^1$ ) by Horibe-Yanagawa’s lemma [1]. The reason for dealing with a banded loop system (κ, β) rather than a banded link (k₀, b) is because not only can a based disk system δ be chosen freely, but it also makes a band deformation of the band system β easier. Actually, an isotopic deformation of β respecting the arc system α₁ and the loop system κ does not change the ribbon surface-link cl( $F_{-\text{1}}^1$ ) in R⁴ and the proper surface ucl( $F_0^1$ ) in $R_{+}^4$ , up to equivalences.

Let cl( $F_{-\text{1}}^1$ )d be the surface-link in R⁴ obtained from the ribbon surface-link cl( $F_{-\text{1}}^1$ ) by surgery along the 2-handle d[−ε, ε] on cl( $F_{-\text{1}}^1$ ) where 0 < ε < t < 1.

The proper surface $P\left(F_0^1\right)=cl(F_{-1}^1)d\cap R_{+}^4$ in $R_{+}^4$ with $\partial P=F_0^1=k$ is called a proper realizing surface of a banded loop system (κ, β) with surgery link k₀ = k ∪ o. The following theorem is known [1].

Normal form theorem: Every compact oriented proper surface F without closed component in the upper-half 4-space $R_{+}^4$ with ∂F = k in R³ is equivalent to a proper realizing surface $P\left(F_0^1\right)$ in $R_{+}^4$ with $\partial P=\left(F_0^1\right)=k$ of a banded loop system (κ, β) with surgery link k₀ = k + o which is a split sum of k and an extra trivial link o.

The proper realizing surface $P\left(F_0^1\right)$ in $R_{+}^4$ is called a normal form of the proper surface F in $R_{+}^4$ . If the extra trivial link o is taken the empty link, namely $P\left(F_0^1\right)=ucl\left(F_0^1\right)$ , then the proper surface F in $R_{+}^4$ is called a ribbon surface. In the following example, it is observed that there are lots of compact oriented proper surfaces without closed component in $R_{+}^4$ which are not equivalent to any ribbon surface in $R_{+}^4$ .

Example. For every link k in R³, let F ′ be any ribbon surface in with k = ∂F ′. For example, let F ′ be a proper surface in $R_{+}^4$ obtained from a Seifert surface for k in R³ by an interior push into $R_{+}^4$ . Take a connected sum F = F ′#K of F ′ and a nontrivial S²-knot K in R⁴ with non-abelian fundamental group. Then k = ∂F ′ = ∂F. It is shown that F is not equivalent to any ribbon surface in $R_{+}^4$ . The fundamental groups of k, F ′, F, K are denoted as follows.

π(k) = π₁(R³ \ k, x₀), π(F′) = π₁(R⁴ \ F′, x₀), π(F) = π₁(R⁴ \ F, x₀), π(K) = π₁(S⁴ \ K, x₀).

Let π(k)*, π(F′)*, π(F′)*, π(K)* be the kernels of the canonical epimorphisms from the groups π(k), π(F′), π(F), π(K) to the infinite cyclic group sending every meridian element to the generator, respectively. It is a special feature of a ribbon surface F′ that the canonical homomorphism π(k) → π(F′) is an epimorphism, so that the induced homomorphism π(k)* → π(F′)* is onto. On the other hand, the canonical homomorphism π(k) → π(F) is not onto, because the group π(F)* is the free product π(F′)* * π(K)* and π(K)* ≠ 0 and the image of the induced homomorphism π(k)* → π(F)* is just the free product summand π(F′)*. Thus, the proper surface F in $R_{+}^4$ is not equivalent to any ribbon surface.

A compact oriented proper surface F′ in $R_{+}^4$ is a renewal embedding of a compact oriented proper surface F in $R_{+}^4$ if there is an orientation-preserving surfacediffeomorphism F′ → F keeping the boundary fixed. A renewal embedding F ′of F is boundary-relative if the link k′ = ∂F ′ in R³ is equivalent to the link k = ∂F in R³. The proof of the following theorem is given [2]. In this paper, an alternative proof of this theorem is given from a viewpoint of deformations of a ribbon surface-link in R⁴.

Classical ribbon theorem: Assume that a link k in the 3-space R³ bounds a compact oriented proper surface F without closed component in the upper-half 4space $R_{+}^4$ . Then the link k in R³ bounds a ribbon surface F ′ in $R_{+}^4$ which is a boundary-relative renewal embedding of F.

A link k in R³ is a slice link in the strong sense if k bounds a proper disk system embedded smoothly in $R_{+}^4$ . A link k in R³ is a ribbon link if k bounds a ribbon disk system in $R_{+}^4$ . The following corollary is a special case of Classical ribbon theorem.

Corollary 1: Every slice link in the strong sense in R³ is a ribbon link.

Thus, Classical ribbon theorem solves Slice-Ribbon Problem, [3,4]. The following corollary is obtained from Corollary 1.

Corollary 2: A link k in R³ is a ribbon link if a ribbon link is obtained from the split sum k + o of k and a trivial link o by a band sum of k and every component of o.

The proof of the classical ribbon theorem is done throughout the section 2. An idea of the proof is to consider the 2-handle pair system (D × I, D′ × I) on the ribbon surface-link cl( $F_{-\text{1}}^1$ ) with k + o as the middle-cross sectional link such that is $P\left(F_0^1\right)$ equivalent to a previously given surface F in $R_{+}^4$ , where the 2-handle system D × I is constructed from the band system b₁ and the 2-handle system D′ × I is constructed from the extra disk system d. The interior intersections of (D × I, D′ × I) will be eliminated and (D × I, D′ × I) becomes an O2-handle pair system on a new ribbon surface-link cl( $F_{-\text{1}}^1$ ) with k + o as the middle-cross sectional link obtained by sacrificing equivalences. Then $P\left(F_0^1\right)$ is a ribbon surface that is a boundary-relative renewal embedding of F, which will complete the proof.

Throughout this section, the proof of the classical ribbon theorem is done. Let F be a compact oriented proper surface without closed component in $R_{+}^4$ , and ∂F = k a link in R³. By the normal form theorem, there is a banded loop system (κ, β) with surgery link k₀ = k + o such that $P\left(F_0^1\right)$ is equivalent to F. The extra trivial link o is uniquely specified by the banded loop system (κ, β), which is the union of the arc system α₁ and the complementary arc system ${\alpha }_1^c$ , where the interior of α₁ transversely meets the interior of a based disk system δ with finite points and is disjoint from the based loop system κ and ${\alpha }_1^c$ belongs to the loop system κ.

A renewal embedding of a banded loop system (κ, β) with surgery link k₀ = k ∪ o is a banded loop system (κ′, β′) with surgery link such that there is a homeomorphism κ ∪ β →κ′ ∪ β′ with restrictios κ → κ′ and β → β′ orientation preserved.

The following observation is directly obtained by definition.

(2.1) If a banded loop system system (κ′, β′) with surgery link k′ ∪ o is a renewal embedding of a banded loop system (κ, β) with surgery link k ∪ o, then the upper-closed realizing surface ucl ${\left(F_0^1\right)}^{\text{'}}$ constructed from (κ′, β′) is a renewal embedding of the upper-closed realizing surface ucl ${\left(F_0^1\right)}^{\text{'}}$ constructed from (κ, β) such that $\partial ucl=\left(F_0^1\right)=k\cup o$ and $\partial ucl=\left(F_0^1\right)\text{'}=k^{\prime }\cup o$ .

A transversal arc of a band spanning a link is a simple proper arc in the band which is parallel to an attaching arc. For a band b ∈ b transversely meeting the interior of an extra disk d ∈ d, the d-arc system of b is the arc system d(b) of every transversal arc a of b in the interior of d. The d-arc system of a band system b is the collection d(b) of d(b) for every d ∈ d and every b ∈ b. For a based disk δ ∈ δ, the δ-arc system of a band β ∈ β is the arc system δ(β) of every transversal arc c of β in the interior of δ. The δ-arc system of β is the collection δ(β) of δ(β) for every δ ∈ δ and every β ∈ β. A normal proper arc in the extra disk system d is a simple proper arc in d with the endpoints in the interior of the arc system α₁. The following assertion is shown.

(2.2) By isotopic deformations in R³, the banded loop system (κ, β) in R³ with surgery link k₀ = k + o is deformed so that a based disk system δ transversely meets the extra disk system d with interior simple arcs or normal proper arcs in d except for the complementary arc system ${\alpha }_1^c$ .

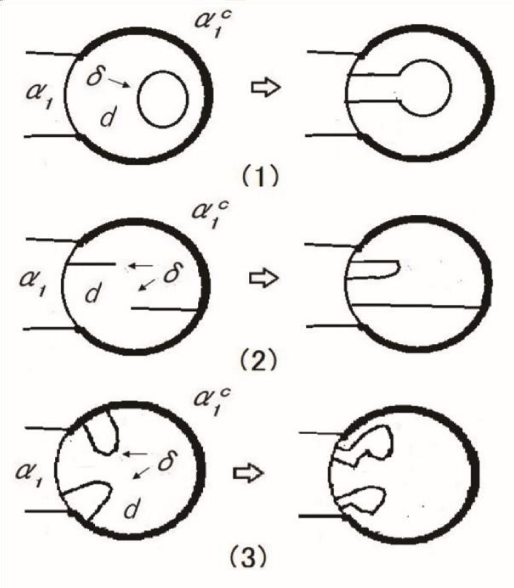
Proof of (2.2). By transverse regularity, the intersection d ∩ δ for every d ∈ d and every δ ∈ δ is made interior simple loops, interior simple arcs, clasp type simple arcs or simple proper arcs in d except for the complementary arc system ${\alpha }_1^c$ . A simple loop is changed into a normal proper arc by a pushing out deformation to α₁, Figure 1(1). A clasp type simple arc is changed into a simple proper arc by moving out the interior point to α₁, Figure 1(2). A simple proper arc which is not normal is also changed into a normal proper arc by a pushing out deformation of the arc system of δ meeting a boundary collar of ${\alpha }_1^c$ in d, Figure 1(3). Thus, a deformed based disk system δ transversely meets d with interior simple arcs or normal proper arcs in d except for the complementary arc system ${\alpha }_1^c$ . This completes the proof of (2.2).

In the proof of (2.2), there is no need to worry about the intersection of the based disk system δ and the interior of the arc system α₁ in R³, because δ is taken and deformed in the 3-spaces R³[±1] and the extra disk system d and the arc system α₁ are taken and fixed in the 3-space R³[0] for the ribbon surface-link cl( $F_{-\text{1}}^1$ ) in R⁴. The following operation gives a standard renewal embedding of a banded loop system.

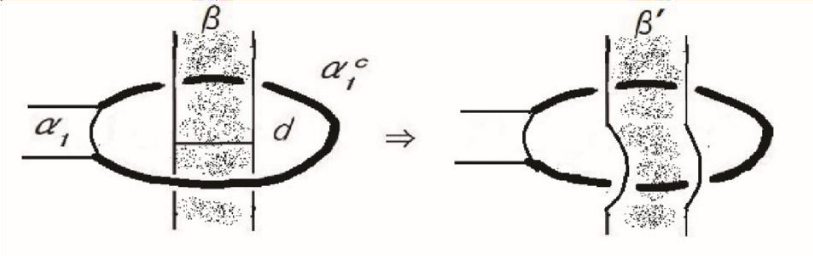
Band move operation: In the banded loop system (κ, β) with surgery link k₀ = k ∪ o, assume that there is a transversal arc c of a band β ∈ β in the interior of an extra disk d ∈ d and there is a simple path ω in d from a point p ∈ c to an interior point of the arc ${\alpha }_1^C=\partial d\cap {\alpha }_1^C$ which avoids meeting β other than c. Let β′be a band obtained from β by sliding the arc c off the disk d along the path ω. Replace the banded loop system (κ, β) with the banded loop system (κ, β′) obtained by replacing β with β′, Figure 2.

By this operation, the new banded loop system (κ, β′) is a renewal embedding of the original banded loop system (κ, β) and has as the surgery link a new union $k_0^{\text{'}}$ of the same links k and o, not necessarily the split sum k + o, because the band system β′is isotopic to β if ${\alpha }_1^c$ is forgotten. In the final stage of this paper, the surgery link $k_0^{\text{'}}=k+o$ will have k ∩ d = ∅, so that $k_0^{\text{'}}$ will be the split sum k + o, because o = ∂d.

To achieve a situation where the Band Move Operation can be applied, the follwing concept is needed. A splitting of a banded loop system (κ, β) is a banded loop system (k*, β*) such that a based disk system δ* for κ* is obtained from a based disk system δ for κ by splitting along a disjoint proper arc system γ in δ not meeting o and β, and the band system β* is obtained from the band system β by adding the band system β_γ thickening γ. This splitting operation comes from Fission-Fusion move of a banded loop system, [5,6]. After some splittings of a banded loop system, a situation where the Band Move Operation can be applied is realized by a replacement of the based disk system and an isotopic deformation of the band system.

The following assertion is used.

(2.3) If there is a splitting (k*, β*) of a banded loop system (κ, β) with surgery knot k₀ a union of k and o such that κ* does not meet the interior of the extra disk system d, then there is a renewal embedding (k′, β′) of (k, β) such that (k′, β′) does not meet the interior of d and has the surgery knot $k_0^{\text{'}}=k+o$ .

Proof of (2.3). Since κ* does not meet the interior of d, there is a based disk system δ* for κ* not meeting the interior of d. The band system β* transversely meets the interior of d with transverse arc system A. Let ${\delta }_1^{*}$ be the sub-system of δ* containing the complementary arc system ${\alpha }_1^c$ in the boundary, and $N({\alpha }_1^C)$ a boundary collar disk system of ${\alpha }_1^c$ in ${\delta }_1^{*}$ . The Band Move Operation means that the band system β* is deformed so that the transverse arc system A moves from the interior of d into the interior of $N({\alpha }_1^C)$ . Then by changing the band system β_γ back into the arc system γ, the banded loop system (k*, β*) is changed back to a pair (k′, β′), where the loop system κ′bounds an immersed disk system δ′obtained from the based disk system δ by moving a transverse arc system of β_γ into the interior of $N({\alpha }_1^C)$ . The immersed disk system δ′is deformed into a disjoint disk system by repeatedly pulling the band in β_γ connecting to an outer most disk of δ* or passing the outer most disk of δ* through $N({\alpha }_1^C)$ in order to eliminate the nearest transverse arc of the band. This means that the loop system κ′is a trivial link and (k′, β′) is a banded loop system. Thus, there is a renewal embedding (k′, β′) of (k, β) which does not meet the interior of d. The surgery knot $k_0^{\text{'}}$ is necessarily the split sum k + o since ∂d = o. This completes the proof of (2.3).

By using (2.2) and (2.3), the following assertion is shown.

(2.4) There is a renewal embedding (κ′, β′) of every banded loop system (κ, β) in R³ with surgery link k₀ = k + o such that (k′, β′) does not meet the interior of d and has the surgery knot $k_0^{\text{'}}=k+o$ .

Proof of (2.4). By (2.2), a based disk system δ of κ transversely meets the extra disk system d with interior simple arcs or normal proper arcs in d except for the complementary arc system ${\alpha }_1^c$ . Let A be the interior arc system which is made disjoint from β by isotopic deformations of β respecting the arc system α₁ and the loop system κ. By taking a splitting of (κ, β) along A, it is considered that the based disk system δ transversely meets d only with normal proper arcs in d except for ${\alpha }_1^c$ . Then κ does not meet the interior of the extra disk system d. By (2.3), the proof of (2.4) is completed.

Let (κ, β) be a banded loop system a banded loop system with surgery link k₀ = k + o such that $P\left(F_0^1\right)$ is equivalent to F. By (2.4), there is a renewal embedding (κ′, β′) such that (κ′, β′) does not meet the interior of the extra disk system d, and has the surgery link k + o. Let b′ be the band system dual to the band system β′, and ${b^{\prime }}_1$ the band sub-system of b′ such that ${b^{\prime }}_1$ connects to o with just one band for every component of o. Let ${b^{\prime }}_2=b^{\prime }\backslash {b^{\prime }}_1$ . Since ${b^{\prime }}_1$ does not meet the interior of d, the surgery link of the banded link $(k+o,b^{\prime })$ is equivalent to the link k and the upper-closed realizing surface ucl $\left(F_0^1\right)\text{'}$ of the banded link $(k,{b^{\prime }}_2)$ is equivalent to the proper realizing surface $P\left(F_0^1\right)\text{'}$ of (κ′, β′) which is a ribbon surface in $R_{+}^4$ and is a renewal embedding of the proper realizing surface $P\left(F_0^1\right)$ of the banded loop system (κ, β) with the surgery link k + o. Since $P\left(F_0^1\right)$ is equivalent to F in $R_{+}^4$ and ucl ${\left(F_0^1\right)}^{\prime }$ is a ribbon surface with $\partial ucl\left(F_0^1\right)\text{'}=\partial F=k$ , there is a boundary-relative renewal embedding from ucl ${\left(F_0^1\right)}^{\prime }$ to F. This completes the proof of the classical ribbon theorem.

The author thanks to a referee for suggesting the content for making easier content. This paper is motivated by T. Shibuya’s comments pointing out insufficient explanation on Lemma 2.3 in [2] (Corollary 2 in this paper). This work was partly supported by JSPS KAKENHI Grant Number JP21H00978 and MEXT Promotion of Distinctive Joint Research Center Program JPMXP0723833165.

1. Kawauchi A, Shibuya T, Suzuki S. Descriptions on surfaces in four-space I: Normal forms. Math Semin Notes Kobe Univ. 1982;10:75–125. Available from: https://www.researchgate.net/publication/268176987_Descriptions_on_surfaces_in_four_space_I_Normal_forms
2. Kawauchi A. Ribbonness on classical link. J Math Tech Comput Math. 2023;2(8):375–7. Available from: https://doi.org/10.48550/arXiv.2307.16483
3. Fox RH. Some problems in knot theory. In: Topology of 3-manifolds and related topics. Engelwood Cliffs (NJ): Prentice-Hall, Inc.; 1962;168–76. Available from: https://ben300694.github.io/pdfs/concordance/%5BFox%5D_Some_Problems_in_Knot_Theory_(1962).pdf
4. Fox RH. Characterization of slices and ribbons. Osaka J Math. 1973;10:69–76.
5. Kawauchi A. A chord diagram of a ribbon surface-link. J Knot Theory Ramifications. 2015;24:1540002. Available from: https://doi.org/10.1142/S0218216515400027
6. Kawauchi A. Ribbonness of a stable-ribbon surface-link, I. A stably trivial surface-link. Topol Appl. 2021;301:107522. Available from: https://doi.org/10.1016/j.topol.2020.107522