In this paper, the concept of ‘system of fuzzy reasoning’ is presented. It is the first temptation to expand ideas presented in [1] concerning ‘human intelligence’ linguistic variable and [2] concerning ‘truth value of fuzzy reasoning’ in the framework of the human intelligence linguistic variable. In ‘systems of fuzzy reasoning’, besides the ‘human intelligence’ linguistic variable also other linguistic variables are also used. An expert knowledge-based system of fuzzy reasoning describing the dynamics of a real-world phenomenon is presented.

Systems of fuzzy reasoning provide a theoretical framework for modelling. First, by defining the concept of system of fuzzy reasoning, its properties, and then by stating the necessary and sufficient conditions to encompass all possible ‘If…THEN …’ statements. Finally, selecting the resulting membership function [3]. pg.81. More statements that are general can be formulated on a system of reasoning than on arbitrary ones. Linguistic variables can often be used to transform non-numerical reasoning premises and responses into a numerical form.

Definition 1.1

A system of fuzzy reasoning $R=\{R_1, R_2,\dots R_I\}$ is a set of fuzzy reasonings R_i

R_i = If(a₁ is A_i1) U+22C8i1 (a₂ is A_i2) ⋈i2 … ⋈ik-1 (a_k is A_iik) then (b_i is B_i) (1.1)

where:

i = 1, … , I, k = 1, … K, A_iik and B_i are triangular or trapezoidal fuzzy subsets of the set of real numbers .

The symbols denoted by ${ℝ}^{\text{1}}$ are fuzzy statements (called by some people arguments), the symbols a₁, a₂, … , a_k are real numbers and are called premises. The symbols denoted by (b_i is B_i) are fuzzy statements, called individual consequences or responses. The symbols bi are real numbers. The membership functions of the fuzzy subsets A_iik and Bi are denoted by $f_{A_{ik}} and f_{B_{i,}}$ respectively. The symbol denoted by ⋈i is one of the fuzzy logic operators: NOT, AND, OR, XOR.

According to [2], the part of the fuzzy logic reasoning R_i (see formula (1.1)) denoted by

(a₁ is A_i1) ⋈i1 (a₂ is A_i2) ⋈i2 … ⋈ik-1 (a_k is A_iik) (1.2)

is called a fuzzy logic expression of R_i.

Remark that, according to this definition, the number of arguments can be different for different logical expressions of the system. Concerning this aspect, we point out that it is possible to formulate all reasoning with a common number K of arguments by ta_king for arguments k, which are not used in rule i, the membership function $f_{A_{ik}}\left(x\right)=1 for all x\in {ℝ}^1.$

To calculate the response of a fuzzy reasoning system = {R₁, R₂, … em>R_I}, the truth value of reasoning R₁ (degree of fulfillment DOF(R₁)) has to be evaluated using a selected inference method. In the next step, the responses of the individual’s reasoning are combined with the help of a combination method. Finally, a defuzzification method transforms the fuzzy reasoning system's response to a crisp result. This procedure can be considered as the definition of a function assigning the final (crisp) result to the input.

The subject of the truth value DOF() of a fuzzy logic reasoning R₁

R₁ = If(a₁ is A_i1) ⋈i1 (a₂ is A_i2) ⋈i2 … ⋈ik-1 (a_k is A_iik) then (b_i is B_i)

is largely discussed in [2], in the framework of the ‘human intelligence’ linguistic variable.

In the following, we expand the truth value computation for a system of fuzzy logic reasoning by using several illustrative examples of such computation.

Example 1.1 (system of two reasonings with one premise) Consider the fuzzy reasoning system R consisting of two reasonings R = {R₁, R₂} and one premise a₁. The reasons are given by

$R_1=If\left(a_{1}is A_{11}\right) then \left(b_1 is B_1\right),A_{11}=\left(1,2,3\right) ,B_1=\left(1,2,3\right) triangular fuzzy subsets$

$R_2=If\left(a_{1}is A_{21}\right) then \left(b_2 is B_2\right),A_{21}=\left(2,3,4\right) , B_2\left(3,4,5\right) triangular fuzzy subsets$

In case of the fuzzy reasoning R₁, the logical expression is the statement (a₁ is a₁1) whose truth value is $f_{A_{11}}\left(a_1\right)=a_1-1 for 1<a_1<2 and f_{A_{11}}\left(a_1\right)=3-a_1 for 2<a_1<3.$

In case of the fuzzy reasoning R₂, the logical expression is the statement (a₁ is a₂₁) whose truth value is $f_{A_{21}}\left(a_1\right)=a_1-2 for 2<a_1<3 and f_{A_{21}}\left(a_1\right)=4-a_1 for 3<a_1<4.$

The normed weighted sum of a combination of individual responses (DOF, B_i) is the overall fuzzy consequence B with the membership function [2] pg.086.

(1.3)

Computing β_i. we find β₁ = β₂ = 1. Hence $f_B\left(x\right)=\frac{f_{A_{11}}\left(a_1\right)\times f_{B_1}\left(x\right)+f_{A_{21}}\left(a_1\right)\times f_{B_2}\left(x\right)}{ma{x}_u[f_{A_{11}}\left(a_1\right)\times f_{B_1}\left(u\right)+f_{A_{21}}\left(a_1\right)\times f_{B_2}\left(u\right)]}.$

For 1 < a₁ < 2 after replacing $f_{A_{11}}\left(a_1\right) , f_{A_{21}}\left(a_1\right)$ the following result is found:

$f_B\left(x\right)=\frac{(a_1-1)\times f_{B_1}\left(x\right)+0\times f_{B_2}\left(x\right)}{ma{x}_u[(a_1-1)\times f_{B_1}\left(u\right)+0\times f_{B_2}\left(u\right)]}=\frac{(a_1-1)\times (x-1)}{ma{x}_u[(a_1-1)\times f_{B_1}\left(u\right)]}=x-1\text{ for } 1<x<2$

$f_B\left(x\right)=\frac{(a_1-1)\times f_{B_1}\left(x\right)+0\times f_{B_2}\left(x\right)}{ma{x}_u[(a_1-1)\times f_{B_1}\left(u\right)+0\times f_{B_2}\left(u\right)]}=\frac{(a_1-1)\times (3-x)}{ma{x}_u[(a_1-1)\times f_{B_1}\left(u\right)]}=3-x\text{ for } 2<x<3$

$f_B\left(x\right)=\frac{\left(a_1-1\right)\times f_{B_1}\left(x\right)+0\times f_{B_2}\left(x\right)}{ma{x}_u\left[\left(a_1-1\right)\times f_{B_1}\left(u\right)+0\times f_{B_2}\left(u\right)\right]}=\frac{0}{ma{x}_u\left[\left(a_1-1\right)\times f_{B_1}\left(u\right)\right]}=0\text{ for } 3<x<4$

$f_B\left(x\right)=\frac{\left(a_1-1\right)\times f_{B_1}\left(x\right)+0\times f_{B_2}\left(x\right)}{ma{x}_u\left[\left(a_1-1\right)\times f_{B_1}\left(u\right)+0\times f_{B_2}\left(u\right)\right]}=\frac{0}{ma{x}_u\left[\left(a_1-1\right)\times f_{B_1}\left(u\right)\right]}=0\text{ for } 4<x<5$

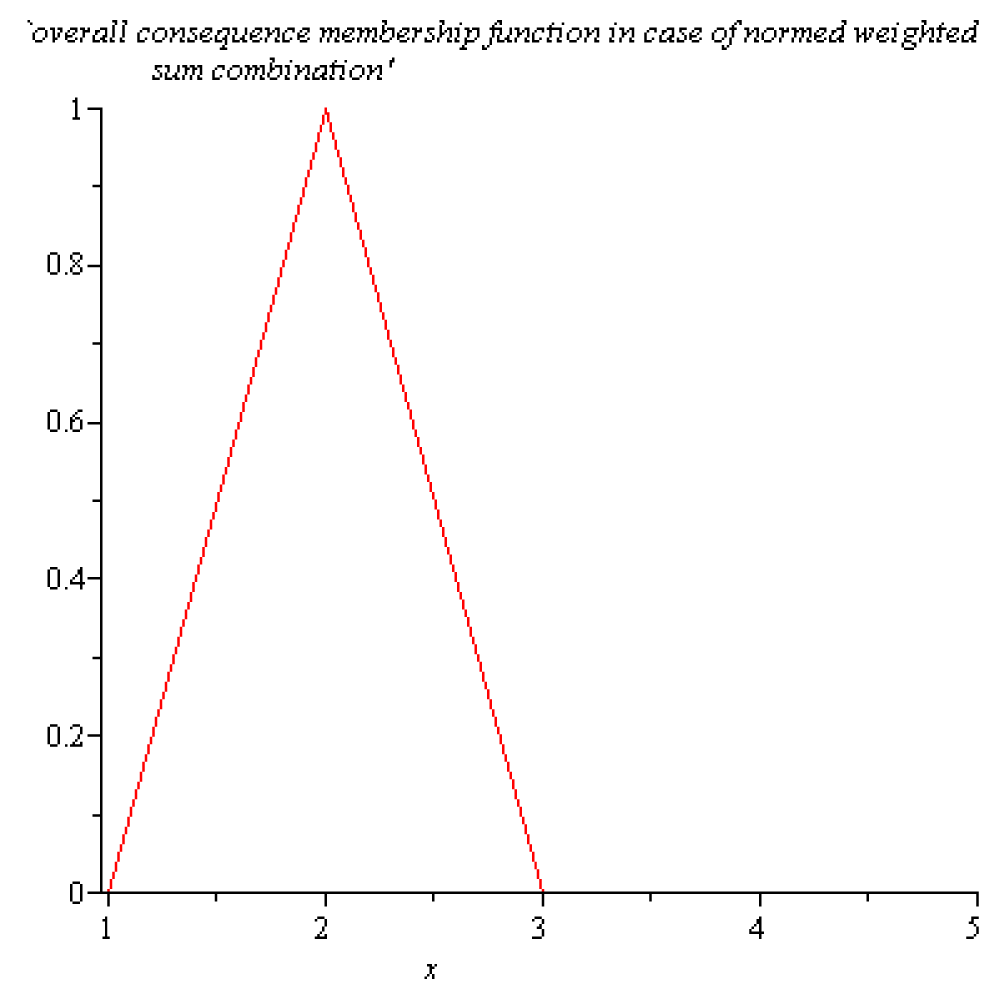
According to [2] p. 086. The membership function f_B(x) of the overall fuzzy consequence B for 1 < a₁ < 3 is the fuzzy subset represented in the next Figure 1.1:

The fuzzy mean of the overall fuzzy consequence B, denoted by M(B), and defined by

$M\left(B\right)=\frac{{{\displaystyle \int }}_{-\infty }^{\infty }x\times f_B\left(x\right)dx}{{{\displaystyle \int }}_{-\infty }^{\infty }{f}_B\left(x\right)dx}$ (1.4)

is the location of the overall fuzzy consequence B. It is also called the center of gravity or centroid. This is the number for which the part of the membership function f_B(x) on the left of this number is in equilibrium with the right side. The equilibria occur when the moments corresponding to the two sides are equal. Computing the fuzzy mean directly by using formula (1.4), the following result is found: M(B) = 2. Therefore, the equilibrium in the case of this example is situated at the point x = 2.

On the other hand, according to [2], when the normed weighted sum combination and mean defuzzification are used, the following equality holds:

$R\left(a_1\right)=M(B)\left(a_1\right)=\frac{{{\displaystyle \sum }}_{i=1}^2{d}_i\times M(B_i)}{{{\displaystyle \sum }}_{i=1}^2{d}_i}$ (1.5)

Where d₁, d₂ are the truth values of the logical expression of the fuzzy reasoning R₁, R₂, respectively, and M(B₁), M(B₂) are the mean value of the individual answers of the fuzzy reasoning R₁, R₂, respectively. In case of the system of fuzzy reasoning R = {R₁, R₂}

For 1 < a₁ < 2, the following equality holds:

d₁ = a₁ -1, d₂ = 0, M(B₁) = 2 M(B₂) = 4

Replacing these values in formula (1.5), it follows that $R\left(a_1\right)=M\left(B\right)\left(a_1\right)=\frac{(a_1-1)\times 2+0\times 4}{a_1-1+0}=2.$

Remark that the localization of equilibrium obtained with (1.5) is the same as that obtained with (1.4) via membership function.

For 2 < a₁ < 3, d₁ = 3 - a₁, d₂ = a₁ - 2, M(B₁) = 2, M(B₂) = 4. Replacing these values in formula (1.5), the following result is found:

$R\left(a_1\right)=M\left(B\right)\left(a_1\right)=\frac{(3-a_1)\times 2+(a_1-2)\times 4}{3-a_1+a_1-2}=2\times a_1-2.$

Therefore, when 2 < a₁ < 3, the equilibrium is located at the point x = 2 × a₁ – 2.

For 3 < a₁ < 4, d₁ = 0, d₂ = 4 - a₁, M(B₁) = 2, M(B₂) = 4. Replacing these values in formula (1.5), the following result is found:

$R\left(a_1\right)=M\left(B\right)\left(a_1\right)=\frac{0\times 2+(4-a_1)\times 4}{0+4-a_1}=4.$

Therefore, when 3 < a₁ < 4, the equilibrium is located at the point x = 4.

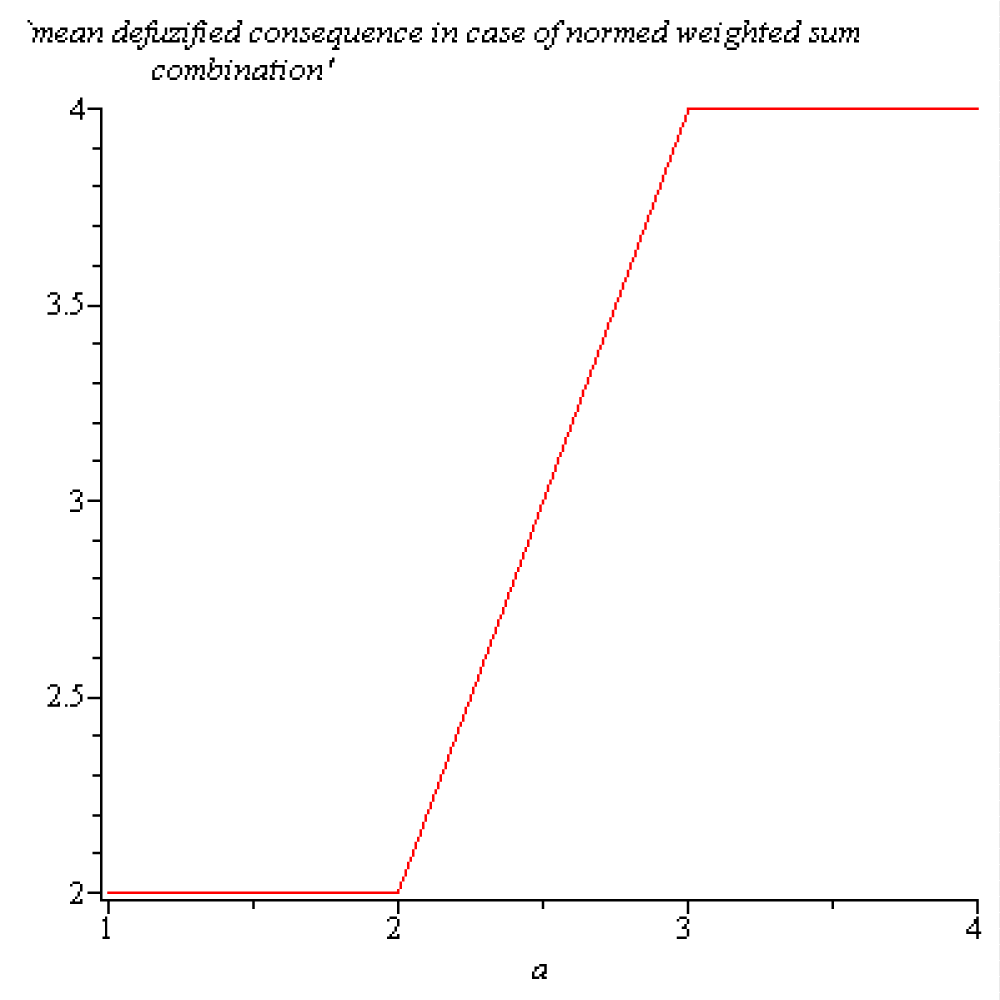
The number R(a₁) = M(B)(a₁), assigning the final (crisp) result to the input a₁, is considered the location of the truth value of the system of fuzzy reasoning R = {R₁, R₂} corresponding to the input a₁. The graphic of the function R(a₁) = M(B)(a₁) is presented in the next Figure 1.2:

Figure 1.2. Show that: for one input a₁ ∈ [1,2] the truth value of the overall response of system is located at 2, for one input a₁ ∈ [2,3] the truth value of the overall response of system is located at 2a₁ - 2, for one input a₁ ∈ [3,4] the truth value of the overall response of system is located at 4. It can be seen that the centroid is constant if a small perturbation of the input a₁ ∈ (1,2) ∪ (3,4) occurs. For input a₁ ∈ [2,3], the truth value location of the overall response of the system increases linearly from 2 to 4. This interval is more appropriate to control the equilibrium location via the premise a₁.

Example 1.2. (Example 4.4. Pg. 90. [1], system of three reasonings with one premise. Consider the fuzzy reasoning system R consisting of the following three fuzzy reasonings, R = {R₁, R₂, R₃}:

$R_1\text{ is }If\left(a is A_1\right) then \left(b_1 is B_1\right),A_1=\left(1,2,3\right) ,B_1=\left(0,1,2\right) triangular fuzzy subsets$

$R_2\text{ is }If\left(a is A_2\right) then \left(b_2 is B_2\right),A_2=\left(3,4,5\right) ,B_2=\left(2,3,4\right) triangular fuzzy subsets$

$R_{3}If\left(a is A_3\right) then \left(b_3 is B_3\right),A_3=\left(0,3,6,\right) ,B_3=\left(0,2,4\right) triangular fuzzy subsets$

The truth values of fuzzy logic expressions of reasoning are:

$DOF{R}_1\left(a\right)=a-1,\text{ for 1}<\text{a}<\text{2};DOF{R}_1\left(a\right)=3-a\text{ for 2}<\text{a}<\text{3}$

$DOF{R}_2\left(a\right)=a-3,\text{ for 3}<\text{a}<\text{4};DOF{R}_2\left(a\right)=5-a\text{ for 4}<\text{a}<\text{5}$

$DOF{R}_3\left(a\right)=\frac{a}{3},\text{ for 0}<\text{a}<\text{3};DOF{R}_3\left(a\right)=\frac{6-a}{3}\text{ for 3}<\text{a}<\text{6}$

On the interval [1,5], the DOFR_i(a) can be written as

$\text{for 1}<\text{a}<\text{2};DOF{R}_1\left(a\right)=a-1, DOF{R}_2\left(a\right)=0 ; DOF{R}_3\left(a\right)=\frac{a}{3};$

$\text{for 2}<\text{a}<\text{3};DOF{R}_1\left(a\right)=3-a, DOF{R}_2\left(a\right)=0 ; DOF{R}_3\left(a\right)=\frac{a}{3};$

$\text{for 3}<\text{a}<\text{4};DOF{R}_1\left(a\right)=0, DOF{R}_2\left(a\right)=a-3 ; DOF{R}_3\left(a\right)=\frac{6-a}{3};$

$\text{for 4}<\text{a}<\text{5};DOF{R}_1\left(a\right)=0, DOF{R}_2\left(a\right)=5-a ; DOF{R}_3\left(a\right)=\frac{6-a}{3};$

On the other hand:

$f_{B_1}(b_1)=b_1;\text{ for }0<b_1<\text{1 }{f}_{B_1}(b_1)=2-b_1;\text{ for 1}<b_1<\text{2}$

$f_{B_2}(b_2)=b_2-2;\text{ for 2}<b_2<\text{3 }{f}_{B_2}(b_2)=4-b_2;\text{ for 3}<b_2<\text{4}$

$f_{B_2}(b_3)=\frac{b_2}{2};\text{ for 0}<b_3<\text{2 }{f}_{B_3}(b_3)=\frac{4-b_2}{2};\text{ for 2}<b_3<\text{4}$

Therefore, considering the normed weighted sum combination with mean defuzzification, the resulting overall consequence location of the fuzzy reasoning system R = {R₁, R₂, R₃}: is defined as the following one variable function R(a) = M(B)(a) (relation 3.3.5 pg.73 [1]:

$R\left(a\right)=\frac{1\times DOF{R}_1\left(a\right)+3\times DOF{R}_2\left(a\right)+2\times DOF{R}_3\left(a\right)}{DOF{R}_1\left(a\right)+DOF{R}_2\left(a\right)+DOF{R}_3\left(a\right)}$ (1.5)

Hence, we obtain:

$\text{for 1}<\text{a}<\text{2 }R\left(a\right)=\frac{1\times (a-1)+3\times 0+2\times \frac{a}{3}}{a-1+0+\frac{a}{3}} = \frac{5\times a-3}{4\times a-3}$

$\text{for 2}<\text{a}<\text{3 }R\left(a\right)=\frac{1\times (3-a)+3\times 0+2\times \frac{a}{3}}{3-a+0+\frac{a}{3}} = \frac{9-a}{9-2\times a}$

$\text{for 3}<\text{a}<\text{4 }R\left(a\right)=\frac{1\times 0+3\times (a-3)+2\times \frac{6-a}{3}}{0+a-3+\frac{6-a}{3}} = \frac{7\times a-15}{2\times a-3}$

$\text{for 4}<\text{a}<\text{5 }R\left(a\right)=\frac{1\times 0+3\times (5-a)+2\times \frac{6-a}{3}}{0+5-a+\frac{6-a}{3}} = \frac{57-11\times a}{21-4\times a}$

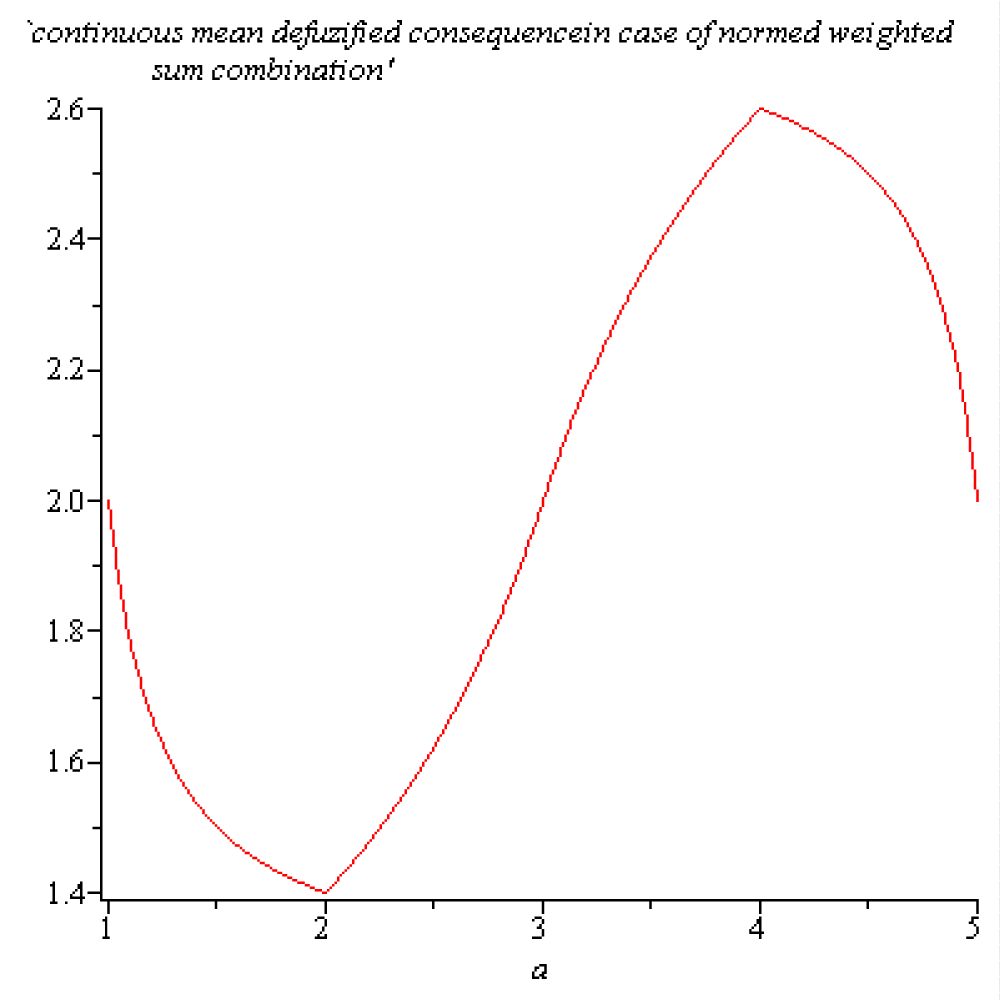
The graphic of the one variable function R(a) = M(B)(a) for a ∈ A is represented in the next Figure 1.3:

Example 1.3 (system of two reasonings with two premises) Consider the fuzzy reasoning system R consisting of two reasonings R = {R₁, R₂} where the reasonings are given by:

$R_{1}If\left(a_{1}is A_{11}\right) then \left(b_1 is B_1\right),A_{11}=\left(1,2,3\right) ,B_1=\left(1,2,3\right) triangular fuzzy subsets$

$R_{2}If\left(a_{2}is A_{22}\right) then \left(b_2 is B_2\right),A_{22}=\left(2,3,4\right) ,B_2=\left(3,4,5\right) triangular fuzzy subsets$

$DOF{R}_1\left(a_1\right)=a_1-1\text{ for 1}<a_1<\text{2; }DOF{R}_1\left(a_1\right)=3-a_1\text{ for 2<}{a}_1<3$

$DOF{R}_1\left(a_2\right)=a_2-2\text{ for 2}<a_2<\text{3; }DOF{R}_2\left(a_2\right)=4-a_2\text{ for 3<}{a}_2<4$

$f_{B_1}(b_1)=b_1\text{ for }1<b_1<\text{2 }{f}_{B_1}(b_1)=3-b_1\text{ for 2}<b_1<\text{3}$

$f_{B2}(b_2)=b_2\text{ for }3<b_2<\text{4 }{f}_{B_2}(b_2)=5-b_2\text{ for 4}<b_2<\text{5}$

For the maximum combination B of B₁, B₂ [2] pg.0.84, the membership function of the overall response is:

$\begin{array}{l}{f}_B\left(b\right)=\text{max}\{DOF{R}_1(a_1)\times f_{B_1}(b),DOF{R}_2(a_2)\times f_{B_2}(b)\}=\\ =\text{ max}\{DOF{R}_1(a_1)\times (b-1),DOF{R}_2(a_2)\times 0\}=\\ =DOF{R}_1(a_1)\times (b-1)\text{ for 1<b<2}\end{array}$

$\begin{array}{l}{f}_B\left(b\right)=\text{max}\{DOF{R}_1(a_1)\times f_{B_1}(b),DOF{R}_2(a_2)\times f_{B_2}(b)\}=\\ =\text{ max}\{DOF{R}_1(a_1)\times (3-b),DOF{R}_2(a_2)\times 0\}=\\ =DOF{R}_1(a_1)\times (3-b)\text{ for 2<b<3}\end{array}$

$\begin{array}{l}{f}_B\left(b\right)=\text{max}\{DOF{R}_1(a_1)\times f_{B_1}(b),DOF{R}_2(a_2)\times f_{B_2}(b)\}=\\ =\text{ max}\{DOF{R}_1(a_1)\times 0,DOF{R}_2(a_2)\times (b-3)\}=\\ =DOF{R}_2(a_2)\times (b-3)\text{ for 3<b<4}\end{array}$

$\begin{array}{l}{f}_B\left(b\right)=\text{max}\{DOF{R}_1(a_1)\times f_{B_1}(b),DOF{R}_2(a_2)\times f_{B_2}(b)\}=\\ =\text{ max}\{DOF{R}_1(a_1)\times 0,DOF{R}_2(a_2)\times (5-b)\}=\\ =DOF{R}_2(a_2)\times (5-b)\text{ for 4<b<5}\end{array}$

The mean value M(B)(a₁,a₂)(centroid or center of gravity) of the defuzzified consequence B, denoted by R(a₁,a₂), is used in multiplicative or additive form for the location of the truth value of the fuzzy reasoning system. In this case, it is:

$R\left(a_1,a_2\right)=DOF{R}_1\left(a_1\right)+2\times DOF{R}_2\left(a_2\right)=(a_1-1)+2\times DOF{R}_2\left(a_2\right) for 1<a_1<2$

and

$R\left(a_1,a_2\right)=DOF{R}_1\left(a_1\right)+2\times DOF{R}_2\left(a_2\right)=(3-a_1)+2\times DOF{R}_2\left(a_2\right) \text{for }2<a_1<3.$

Therefore:

$R\left(a_1,a_2\right)=(a_1-1)+2\times (a_2-2) for 1<a_1<2 and 2<a_2<3$

$R\left(a_1,a_2\right)=(a_1-1)+2\times (4-a_2) for 1<a_1<2 and 3<a_2<4$

$R\left(a_1,a_2\right)=(3-a_1)+2\times (a_2-2) for 2<a_1<3 and 2<a_2<3$

$R\left(a_1,a_2\right)=(3-a_1)+2\times (4-a_2) for 2<a_1<3 and 3<a_2<4$

The location R(a₁, a₂), of the truth value of the fuzzy reasoning system in the case of the overall answer is presented in the next Figure 1.4:

Other combinations can also be used. Using, for example, normed weighted sum combination and mean defuzzification, the overall response location can be obtained directly by using the formula:

$R\left(a_1,a_2\right)=M(B)\left(a_1,a_2\right)=\frac{{{\displaystyle \sum }}_{i=1}^2{d}_i\times M(B_i)}{{{\displaystyle \sum }}_{i=1}^2{d}_i}$ (1.6)

Where d₁, d₂ are the truth values of the logical expression of the fuzzy reasoning R₁, R₂, respectively, and M(B₁), M(B₂) are the mean value of the individual answers of the fuzzy reasoning R₁, R₂, respectively. In case of the same system of reasoning

$R_{1}If\left(a_{1}is A_{11}\right) then \left(b_1 is B_1\right),A_{11}=\left(1,2,3\right) ,B_1=\left(1,2,3\right) triangular fuzzy subsets$

$R_{2}If\left(a_{2}is A_{22}\right) then \left(b_2 is B_2\right),A_{22}=\left(2,3,4\right) ,B_2=\left(3,4,5\right) triangular fuzzy subsets$

Using the already computed truth values

$d_1=DOF{R}_1\left(a_1\right)=a_1-1\text{ for 1<}{a}_1<2;DOF{R}_1\left(a_1\right)=3-a_1\text{ for 2}<a_1<3$

$d_2=DOF{R}_2\left(a_2\right)=a_2-2\text{ for 2<}{a}_2<3;DOF{R}_2\left(a_2\right)=4-a_2\text{ for 3}<a_2<4$

and the values of M(B₁) = 2, M(B₂) = 4 computed using formula

$M\left(B_i\right)=\frac{{{\displaystyle \int }}_{-\infty }^{\infty }x\times f_{B_i}\left(x\right)dx}{{{\displaystyle \int }}_{-\infty }^{\infty }{f}_{B_i}\left(x\right)dx}i\text{ = 1,2}$ (1.7)

and replacing in (1.6), for the overall responses R(a₁, a₂) = M(B)(a₁, a₂), the following result is found:

$R\left(a_1,a_2\right)=\frac{2\times \left(a_1-1\right)+4\times (a_2-2)}{a_1+a_2-3}=\frac{2\times a_1+4\times a_2-10}{a_1+a_2-3}\text{ for 1}<a_1<2\text{ and 2}<a_2<3$

$R\left(a_1,a_2\right)=\frac{2\times \left(a_1-1\right)+4\times (4-a_2)}{a_1-a_2+3}=\frac{2\times a_1-16\times a_2+14}{a_1-a_2+3}\text{ for 1}<a_1<2\text{ and 3}<a_2<4$

$R\left(a_1,a_2\right)=\frac{2\times \left(3-a_1\right)+4\times (a_2-2)}{-a_1+a_2+1}=\frac{-2\times a_1+4\times a_2-2}{-a_1+a_2+1}\text{ for 2}<a_1<3\text{ and 2}<a_2<3$ (1.8)

A system of fuzzy reasoning is complete or consistent on a set of premises A if it can provide an answer to all possible questions concerning the phenomenon modeled, see[3], pg.82. More precisely:

Definition 2.1. The system of fuzzy reasoning

$R=\{R_1, R_2,\dots R_I\}$

is complete on the set ofpremises A if for every premise $(a_1,a_2,\dots a_K)\in A$ the corresponding and the combined response set $B(a_1,a_2,\dots a_K)$ is a nonempty fuzzy set.

Note that the definition requires not only that for every premise $(a_1,a_2,\dots a_K)\in A$ there should be a reasoning i with a non-empty response, but it also requires the combined response to be non-empty. The completeness of a system of fuzzy reasoning depends on the set of premises A on which the reasoning system's responses are to be found, and on the combination method used. The defuzzification does not influence the completeness of the reasoning system. The minimum combination seeks the difficult task of finding complete agreement, while the other methods only exclude responses that are impossible for each rule. Therefore, it is not surprising that the condition of completeness is easier to fulfill using the maximum or additive combination methods than using the minimum one. For a system of fuzzy reasoning, the following statements can be formulated regarding completeness.

Statement 2.1. [3]. pg.83. The fuzzy reasoning system $R=\{R_1, R_2,\dots R_I\},$ used with maximum or additive combination method is complete on the premises set A if and only if for each premise $(a_1,a_2,\dots a_K)\in A$ there is a reasoning Ri such that $DOF(R_i)(a_1,a_2,\dots a_K)>0.$

Statement 2.2. [3]. pg.83. The system of fuzzy reasoning used with the minimum combination method, is complete on the premises set A if and only if

1. for each premise $(a_1,a_2,\dots a_K)\in A$ there is a reasoning R_i such that $DOF(R_i)(a_1,a_2,\dots a_K)>0$

and

2. For any couple of two rules R_i and R_j. if there is $(a_1,a_2,\dots a_K)\in A$ such that $DOF\left(R_i\right)(a_1,a_2,\dots a_K)>0 and DOF(R_j)(a_1,a_2,\dots a_K)>0,$ then $B_i{{\displaystyle \cap }}^{\text{}}{B}_j\ne \varnothing .$

If the minimum combination is used, then the fuzzy reasoning system considered in Example 1.3 is not complete on the interval A = [2,3]. That is because for any $a_1\in A the equality \min \left\{f_{B_1}\left(a_1\right), f_{B_2}\left(a_1\right)\right\}=0 hold.$

If the maximum combination or additive combination is used, then the fuzzy reasoning system considered in Example 1.3 is complete on the interval A = [2,3].

The completeness of a system of fuzzy reasoning used with maximum or additive combinations depends only on the ‘range’ on which the arguments are defined. This ‘range’, which is called the support of a system of fuzzy reasoning, is defined as follows:

Definition 2.3. The support of the fuzzy reasoning

R_i = If(a₁ is A_i1) ⋈i1 (a₂ is A_i2) U+22C8i2 … U+22C8ik-1 (a_k is em> A_iik) then (b_i is B_i)

Is the K - dimesional set defined by

$supp(R_i)=supp\left(A_{i1}\right)\times \dots \times supp\left(A_{iK}\right)$

Statement 2.3. [3].pg.84.The system of fuzzy reasoning $R=\{R_1, R_2,\dots R_1\},$ used with maximum or additive combinations, is complete on A if and only if

$A\subset {{{\displaystyle \cup }}^{\text{}}}_{i=1}^{i=I}supp(R_i).$

Statement 2.4. [3].pg.86.The system of fuzzy reasoning $R=\{R_1, R_2,\dots R_I\}$ used with maximum or additive combinations is complete on $A={{{\displaystyle \cup }}^{\text{}}}_{i=1}^{i=I}supp(R_i).$

The overlap between the premises is an important property of fuzzy reasoning systems. It thus seems that general fuzzy reasoning systems may be at least partly redundant. However, this is not true: even reasoning whose premises are completely covered by other reasoning might still modify the consequences. Therefore, the possibility of removing fuzzy reasoning from a general fuzzy reasoning system without a major change in the consequence cannot be judged based on only the premises. It should be done by comparing the response set. In order to know which fuzzy rules can be removed, a measure of the overlap was defined. For more details, see [1]. Pg. 87. In the following, we intend to give an illustrative example concerning what happens if a fuzzy rule is removed.

Example 2.1. ([3].86). Consider the general fuzzy reasoning system R consisting of three reasoning $R=\{R_1, R_2, R_3\}$ where the reasoning is given by:

$R_1=If\left(a_{1}is A_{11}\right) then \left(b_1 is B_1\right),A_{11}=\left(1,2,3\right),B_1=\left(0,2,4\right) triangular fuzzy subsets$

$R_2=If\left(a_{1}is A_{21}\right) then \left(b_2 is B_2\right),A_{21}=\left(2,3,4\right) ,B_1=\left(3,5,7\right) triangular fuzzy subsets$

$R_3=If\left(a_{1}is A_{31}\right) then \left(b_3 is B_3\right),A_{31}=\left(1.5,2.5,3.5\right),B_3=\left(1,3,5\right) triangular fuzzy subsets$

The premise of the third reasoning is fully covered by the premises of the other two reasonings. The fuzzy reasoning system would remain complete (even for the minimum combination) on A = [1.5,2.5] if the third rule were removed. On the other hand, the consequence of using mean defuzzification and additive combination with

$a_1=2.5 leads to 3.25 and removing R_3 gives 3.5$

Assessment of fuzzy reasoning is a procedure where knowledge and / or available data are translated or encoded in fuzzy reasoning. Since fuzzy reasoning system responses both on the combination and defuzzification method applied, this choice has to be ta_ken into account in the assessment.

According to [3], at least four different ways to assess a fuzzy reasoning system may be distinguished:

a) The fuzzy reasoning system is known by the experts and can be defined directly.

b) The fuzzy reasoning system can be assessed by experts directly, but available data should be used to update it.

c) The fuzzy reasoning system is not known explicitly, but the variables required for the description of the system can be specified by experts.

d) Only a set of observations is available, and a fuzzy reasoning system has to be constructed to describe the interconnection between the input/output elements of the data set.

In this section, we will provide a system of fuzzy reasoning based on expert knowledge.

Consider algae growth in a water body receiving a steady loading of nutrients, including dissolved oxygen. It has been observed that available nutrients x and algae biomass y vary in time and oscillate. Let x and y be measured on the scale between 0 and 1. For the fuzzy reasoning construction, let only two state descriptors, high h and low l, be used. For describing the process in terms of a system of fuzzy reasoning, let us consider the expert knowledge incorporated in the following two triangular fuzzy numbers defined on the unit interval [0,1]:

$A_h=(0.4,0.9,1)A_l=(0,0.1,0.7)$ (3.1)

With respect means:

$M\left(A_h\right)=\frac{2.3}{3}=0.76 M\left(A_l\right)=\frac{0.8}{3}=0.27$ (3.2)

According to experts, the transitions between the states can be described as: starting with states $hh=\left(xis{A}_h\right)AND\left(yis{A}_h\right)$ at moment t, the level of available nutrients and algae is h. In the next time of period (let say 1 unit) the following process ta_ke place: algae reduce nutrients to $states lh=\left(xis{A}_l\right)AND\left(yis{A}_h\right);$ in turn because nutrients are insufficient algae become $l states ll=\left(xis{A}_l\right)AND\left(yis{A}_l\right);$ the nutrients are replenished and become $h state hl=\left(xis{A}_h\right)AND\left(yis{A}_l\right);$ in the next period again algae become $h state hh=\left(xis{A}_h\right)AND\left(yis{A}_h\right).$ Schematically:

$hh\to lh\to ll\to hl\to hh.$ (3.3)

This description is fuzzy, and to describe the process in terms of a system of fuzzy reasoning, let us consider the following system of fuzzy reasoning:

$R_{hh} is If \left(xis{A}_h\right)AND\left(yis{A}_h\right)then\left(xis{A}_l\right)AND\left(yis{A}_h\right)$

$R_{lh} is If \left(xis{A}_l\right)AND\left(yis{A}_h\right)then\left(xis{A}_l\right)AND\left(yis{A}_l\right)$ (3.4)

$R_{ll} is If \left(xis{A}_l\right)AND\left(yis{A}_l\right)then\left(xis{A}_h\right)AND\left(yis{A}_l\right)$

$R_{hl} is If \left(xis{A}_h\right)AND\left(yis{A}_l\right)then\left(xis{A}_h\right)AND\left(yis{A}_h\right)$

The system of fuzzy reasoning (3.4) is an algae growth model and can be used to construct the state vector trajectory in a continuous space for a given initial state (x(0), y(0)). This trajectory is unique.

To illustrate the above proposition, consider the mean defuzzification and the normed weighted sum combination method

$R(a)=\frac{{{\displaystyle \sum }}_{i=1}^{4}M(B_i)\times DOF(R_i\left(a\right))}{{{\displaystyle \sum }}_{i=1}^{4}DOF(R_i\left(a\right))}$ (3.5)

Since in all reasoning the product fuzzy logic operator AND is used in formula (3.5), we replace:

$DOF{R}_1\left(a\right)=DOF{R}_1\left(x,y\right)=(DOF\left(\left(xis{A}_h\right)AND\left(yis{A}_h\right)\right)=f_{A_h}\left(x\right)\times f_{A_h}\left(y\right),$

$DOF{R}_2\left(a\right)=DOF{R}_2\left(x,y\right)=DOF\left(\left(xis{A}_l\right)AND\left(yis{A}_h\right)\right)=f_{A_l}\left(x\right)\times f_{A_h}\left(y\right),$ (3.6)

$DOF{R}_3\left(a\right)=DOF{R}_3\left(x,y\right)=DOF\left(\left(xis{A}_l\right)AND\left(yis{A}_l\right)\right)=f_{A_l}\left(x\right)\times f_{A_l}\left(y\right),$

$DOF{R}_4\left(a\right)=DOF{R}_4\left(x,y\right)=DOF\left(\left(xis{A}_h\right)AND\left(yis{A}_l\right)\right)=f_{A_h}\left(x\right)\times f_{A_l}\left(y\right);$

Remark that he membership functions $f_{A_h}\left(x\right) and f_{A_l}\left(x\right)$ are given:

$f_{A_h}\left(x\right)=0 for x<0.4,f_{A_h}\left(x\right)=\frac{x-0.4}{0.5} for 0.4< x<0.9, f_{A_h}\left(x\right)=\frac{1-x}{0.1} for 0.9< x<1$

$f_{A_h}\left(x\right)=0 for 1<x$ (3.7)

$f_{A_l}\left(x\right)=0 for x<0,f_{A_l}\left(x\right)=\frac{x}{0.1} for 0< x<0.1 , f_{A_l}\left(x\right)=\frac{0.7-x}{0.6} for 0.1< x<0.7$

$f_{A_l}\left(x\right)=0 for 0.7<x$ (3.8)

For the initial state x = 0.5, y = 0.6 the membership values are:

$f_{A_h}\left(0.5\right)=\frac{0.5-0.4}{0.5}=\frac{1}{5}=0.200000000,f_{A_l}\left(0.5\right)=\frac{0.7-0.5}{0.6}=\frac{0.2}{0.6}=\frac{1}{3}=0.333333333;$ (3.9)

$f_{A_h}\left(0.6\right)=\frac{0.6-0.4}{0.5}=\frac{2}{5}=0.4000000000,f_{A_l}\left(0.6\right)=\frac{0.7-0.6}{0.6}=\frac{0.1}{0.6}=\frac{1}{6}= 0.166666666\text{'}$

And the DOF - s values appearing in (3.6) are:

In case of nutrients x, the mean values M(B_i) of individual consequences are replaced by

$\begin{array}{l}M\left(B_1\right)=M\left(A_l\right)=0.27, M\left(B_2\right)=M\left(A_l\right)=0.27 , \\ M\left(B_3\right)=M\left(A_h\right)=0.76,M\left(B_4\right)=M\left(A_h\right)=0.76\end{array}$ (3.10)

In case of algae y, the mean values M(B_i) of individual consequences are replaced by

$\begin{array}{l}M\left(B_1\right)=M\left(A_h\right)=0.76,\left(B_2\right)=M\left(A_l\right)=0.27 , \\ M\left(B_3\right)=M\left(A_l\right)=0.27 ,M\left(B_4\right)=M\left(A_h\right)=0.76\end{array}$ (3.11)

obtaining:

$\begin{array}{l}x(1)=\frac{f_{A_h}\left(x\right)\times f_{A_h}\left(y\right)\times 0.27+f_{A_l}\left(x\right)\times f_{A_h}\left(y\right)\times 0.27+f_{A_l}\left(x\right)\times f_{A_l}\left(y\right)\times 0.76+f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)\times 0.76}{f_{A_h}\left(x\right)\times f_{A_h}\left(y\right)+f_{A_l}\left(x\right)\times f_{A_h}\left(y\right)+f_{A_l}\left(x\right)\times f_{A_l}\left(y\right)+f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)}=\\ \frac{0.02160000000+0.03599999999+0.04222222223+0.02533333334}{0.08000000000+0.1333333333+0.05555555556+0.03333333334}=0.4141176472\end{array}$ (3.12)

$\begin{array}{l}y\left(1\right)=\frac{f_{A_h}\left(x\right)\times f_{A_h}\left(y\right)\times 0.76+f_{A_l}\left(x\right)\times f_{A_h}\left(y\right)\times 0.27+f_{A_l}\left(x\right)\times f_{A_l}\left(y\right)\times 0.27+f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)\times 0.76}{f_{A_h}\left(x\right)\times f_{A_h}\left(y\right)+f_{A_l}\left(x\right)\times f_{A_h}\left(y\right)+f_{A_l}\left(x\right)\times f_{A_l}\left(y\right)+f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)}=\\ \frac{0.02160000000+0.03599999999+0.01500000000+0.02533333334}{0.08000000000+0.1333333333+0.05555555556+0.03333333334}=0.453749999\text{'}\end{array}$ (3.13)

The same procedure is used to obtain x(t+1), y(t+1) as function of x(t), y(t) for t = 1,2,…

For computing the state (x(2),y(2)) we have to start with the initial values $(x\left(1\right),y(1))=(0.4141176472,0.453749999\text{'})$ and compute the following DOF - s

$\begin{array}{l}DOF\left(\left(0.4141176472 is{A}_h) AND (0.4537499999is A_h\right)\right)=f_{A_h}\left(0.4141176472\right)\times \\ f_{A_h}\left(0.4537499999\right)=\frac{0.4141176472-0.4}{0.5}\times \frac{0.4537499999-0.4}{0.5}=0.003035294142,\end{array}$

$\begin{array}{l}DOF(\left(0.4141176472 is{A}_l) AND (0.4537499999 is A_h \right))= f_{A_l}(0.4141176472)\times \\ f_{A_h}\left(0.4537499999\right)=\frac{0.7-0.4141176472}{0.6}\times \frac{0.4537499999-0.4}{0.5}=0.05122058810\end{array}$

$\begin{array}{l}DOF\left(\left(0.4141176472is{A}_l\right)AND\left(0.4537499999 is{A}_l\right)\right)=f_{A_l}\left(0.4141176472\right)\times \\ f_{A_l}\left(0.4537499999\right)=\frac{0.7-0.4141176472}{0.6}\times \frac{0.7-0.4537499999}{0.6}=0.1955514706\end{array}$

$\begin{array}{l}DOF\left(\left(0.4141176472 is A_h\right)AND\left(0.4537499999 is A_l\right)\right)=f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)\\ =\frac{0.4141176472-0.4}{0.5}\times \frac{0.7-0.4537499999}{0.6}=0.0\text{1158823541}\end{array}$

In case of nutrients x, the mean values The same procedure is used to obtain of individual consequences will be replaced by

$\begin{array}{l}M\left(B_1\right)=M\left(A_l\right)=0.27, M\left(B_2\right)=M\left(A_l\right)=0.27 , \\ M\left(B_3\right)=M\left(A_h\right)=0.76,M\left(B_4\right)=M\left(A_h\right)=0.76\end{array}$

In case of algae y, the mean values The same procedure is used to obtain of individual consequences will be replaced by

$\begin{array}{l}M\left(B_1\right)=M\left(A_h\right)=0.76,M\left(B_2\right)=M\left(A_l\right)=0.27 , \\ M\left(B_3\right)=M\left(A_l\right)=0.27 ,M\left(B_4\right)=M\left(A_h\right)=0.76\end{array}$

obtaining:

$x(2)=\frac{f_{A_h}\left(x\right)\times f_{A_h}\left(y\right)\times 0.27+f_{A_l}\left(x\right)\times f_{A_h}\left(y\right)\times 0.27+f_{A_l}\left(x\right)\times f_{A_l}\left(y\right)\times 0.76+f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)\times 0.76}{f_{A_h}\left(x\right)\times f_{A_h}\left(y\right)+f_{A_l}\left(x\right)\times f_{A_h}\left(y\right)+f_{A_l}\left(x\right)\times f_{A_l}\left(y\right)+f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)}=0.6582944494$ (3.14)

$y\left(2\right)=\frac{f_{A_h}\left(x\right)\times f_{A_h}\left(y\right)\times 0.76+f_{A_l}\left(x\right)\times f_{A_h}\left(y\right)\times 0.27+f_{A_l}\left(x\right)\times f_{A_l}\left(y\right)\times 0.27+f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)\times 0.76}{f_{A_h}\left(x\right)\times f_{A_h}\left(y\right)+f_{A_l}\left(x\right)\times f_{A_h}\left(y\right)+f_{A_l}\left(x\right)\times f_{A_l}\left(y\right)+f_{A_h}\left(x\right)\times f_{A_l}\left(y\right)}=0.2974125877$ (3.15)

For computing the state (x(3), y(3)) we have to start with the initial values (x(2), y(2)) = (0.6582944494, 0.2974125877) and compute the following DOF - s

$\begin{array}{l}DOF\left(\left(0.6582944494 is{A}_h) AND (0.2974125877)is A_h\right)\right)=\\ f_{A_h}\left(0.6582944494\right)\times f_{A_h}\left(0.2974125877)\right)=\frac{0.6582944494-0.4}{0.5}\times 0=0,\end{array}$

$\begin{array}{l}DOF(\left(0.6582944494 is{A}_l) AND ( 0.2974125877 is A_h \right))= \\ f_{A_l}(0.6582944494)\times f_{A_h}\left(0.2974125877\right)=\frac{0.6582944494-0.4}{0.5}\times 0=0\end{array}$

$\begin{array}{l}DOF\left(\left(0.6582944494 is A_h\right)AND\left(0.2974125877 is A_l\right)\right)=f_{A_h}\left(0.6582944494\right)\times \\ f_{A_l}\left(0.2974125877\right)=\frac{0.6582944494-0.4}{0.5}\times \frac{0.7-0.2974125877}{0.6}=0.01158823541\end{array}$

For nutrients x using the mean values M(B_i) of individual consequences

$\begin{array}{l}M\left(B_1\right)=M\left(A_l\right)=0.27, M\left(B_2\right)=M\left(A_l\right)=0.27 ,\\ M\left(B_3\right)=M\left(A_h\right)=0.76,M\left(B_4\right)=M\left(A_h\right)=0.76\end{array}$

The computed value of x(3) is x(3) = 0.7599999999

For algae y, using the M(B_i) of individual consequences will be replaced by

$\begin{array}{l}M\left(B_1\right)=M\left(A_h\right)=0.76,M\left(B_2\right)=M\left(A_l\right)=0.27 , \\ M\left(B_3\right)=M\left(A_l\right)=0.27 ,M\left(B_4\right)=M\left(A_h\right)=0.76\end{array}$

The computed value of y(3) is y(3) = 0.7018876635

For computing the state (x(4), y(4)) we have to start with the initial values (x(3), y(3)) = (0.7599999999,0.7018876635) and compute the following DOF – s

$\begin{array}{l}DOF\left(\left(0.7599999999is{A}_h) AND (0.7018876635is A_h\right)\right)=\\ f_{A_h}\left(0.7599999999\right)\times f_{A_h}(0.7018876635)=0.1173739235,\end{array}$

$DOF(\left(0.7599999999is{A}_l) AND ( is A_h \right))= f_{A_l}(0.7599999999)\times f_{A_h}\left(0.7018876635\right)=0$

$DOF\left(\left(0.7599999999is{A}_l\right)AND\left(0.7018876635 is{A}_l\right)\right)=f_{A_l}\left(0.7599999999\right)\times f_{A_l}\left(0.7018876635\right)=0$

$DOF\left(\left( 0.7599999999is A_h\right)AND\left( 0.7018876635is A_l\right)\right)=f_{A_h}\left(0.7599999999\right)\times f_{A_l}\left(0.7018876635\right)=0$

For nutrients x using the mean values M(B_i) of individual consequences

$\begin{array}{l}M\left(B_1\right)=M\left(A_l\right)=0.27, M\left(B_2\right)=M\left(A_l\right)=0.27 , \\ M\left(B_3\right)=M\left(A_h\right)=0.76,M\left(B_4\right)=M\left(A_h\right)=0.76\end{array}$

The computed value of x(4) is x(4) = 0.2699999999

For algae y, using the M(B_i) of individual consequences will be replaced by

$\begin{array}{l}M\left(B_1\right)=M\left(A_h\right)=0.76,M\left(B_2\right)=M\left(A_l\right)=0.27 , \\ M\left(B_3\right)=M\left(A_l\right)=0.27 ,M\left(B_4\right)=M\left(A_h\right)=0.76\end{array}$

The computed value of y(4) is y(4) = 0.7599999999

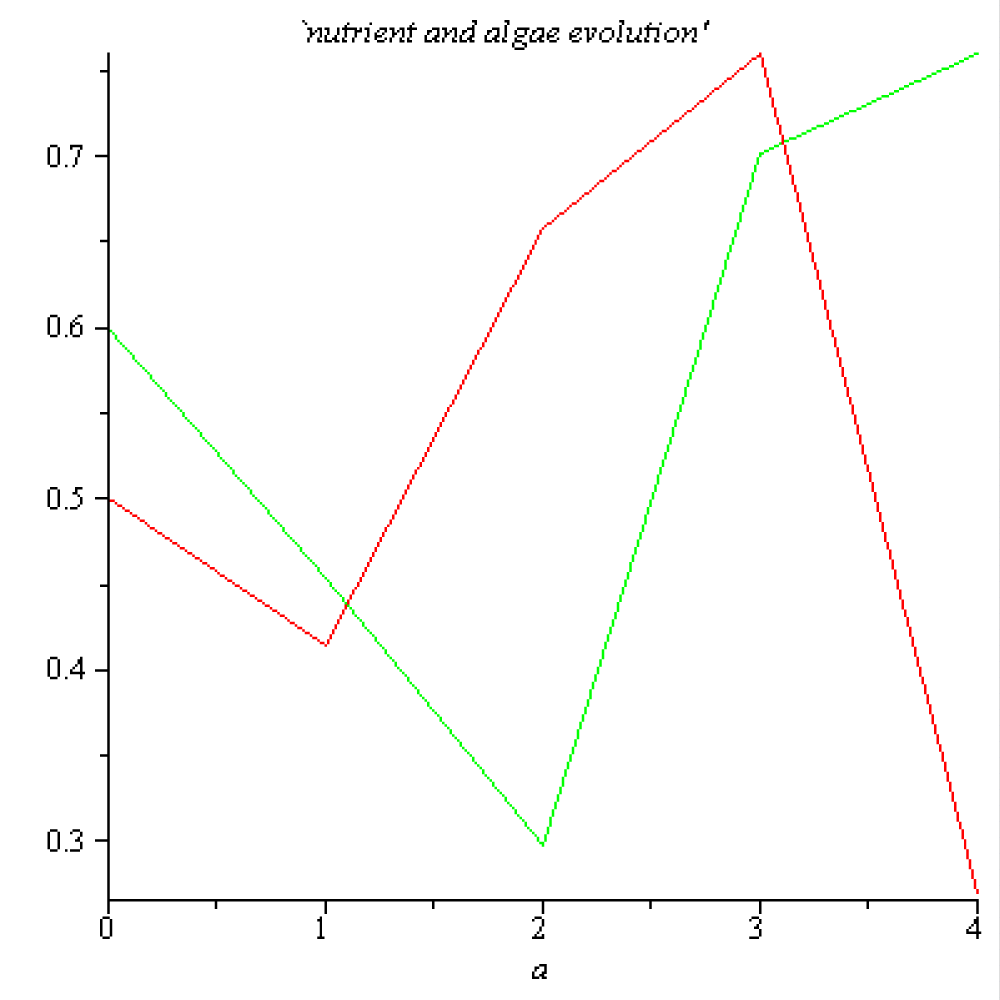
The dynamics of the nutrient evolution and that of the algae evolution during the first four steps are represented in the next Figure 3.1.

For other descriptions, with a system of fuzzy reasoning, of dynamics of real-world phenomena, [4-8].