More Information
Submitted: July 22, 2025 | Approved: July 24, 2025 | Published: July 25, 2025
How to cite this article: Yamamoto T. Coupling Physiology. Int J Phys Res Appl. 2025; 8(7): 247-250. Available from:
https://dx.doi.org/10.29328/journal.ijpra.1001130
DOI: 10.29328/journal.ijpra.1001130
Copyright license: © 2025 Yamamoto T. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is propeRLy cited.
Keywords: Energy simulation; CFD; Heat and mass transfer; Brain
Coupling Physiology
Tatsuhiro Yamamoto*
Kyushu University, Japan
*Address for Correspondence: Tatsuhiro Yamamoto, Kyushu University, Japan, Email: [email protected]; [email protected]
In building science, modelling human Chrono-physiology has progressed from basic two-node systems to detailed frameworks like JOS-3, which incorporate deep body and skin temperature layers to better simulate unsteady thermal states. Despite its significance, deep body temperature is paradoxically treated as a fixed set point, thereby limiting the realism of physiological simulations. Fluid-structure interaction (FSI) techniques offer insight into vascular shear stress but are constrained by computational challenges. Therefore, this study advocates for a more practical approach to human thermal analysis using coupled models that integrate computational fluid dynamics (CFD) and Chrono-physiology. Meshing complexities hinder whole-body CFD modelling, prompting the need for accessible macroscopic frameworks. Central to this research is the redefinition of “heat” in human-environment interactions. Demonstration cases evaluate vascular behavior under muscle activity using simplified equations and dimensionless heat flow metrics. By considering dynamic vessel deformation and adiabatic conditions, the study proposes a methodology for future hybrid models bridging physiology and environmental heat transport. These findings support the development of novel computational models for diverse applications, from building science to sports engineering. The proposed metrics show promise in enhancing predictive accuracy without requiring full-scale FSI computations, offering a foundational step toward three-dimensional physiological simulations.
In the field of building science, the analysis of human Chrono-physiology has received attention, with models evolving from the development of two-node systems [1] to more versatile frameworks such as JOS-3 [2]. These models extend from deep body temperature nodes to the surface layers of the skin, reflecting the importance of detailed physiological representation. The construction of such physical models is fundamentally aimed at reproducing unsteady states, and with systems comprising as many as sixteen nodes, validation of their accuracy is notably challenging. Although deep body temperature is one of the most critical parameters—often treated as a set point—it is paradoxically considered a known value, thus hindering the accurate reproduction of human physiological phenomena.
While the blood flow in vessels is a crucial factor, and fluid-structure interaction (FSI) [3] analysis for evaluating shear stress has become common, its practical application remains limited due to theoretical and computational complexities. Therefore, it is necessary to consider what kind of computational approach to human Chrono-physiology is truly desirable, which leads to the relevance of coupled analysis.
In computational fluid dynamics (CFD), the complexity of meshing makes it extremely difficult to conduct a comprehensive analysis of the entire human body. Thus, by extending unsteady analysis models, this study proposes to establish theoretical frameworks and macroscopic models that are more accessible for practical use in a wide range of applications. How "heat" is conceptualized is of paramount importance for developing future coupled analysis approaches, and this study aims to elucidate the essential methodologies required for such advancements. Building on the preceding discussion, future advances in human Chrono-physiology modeling hinge on a rigorous reconceptualization of heat transfer mechanisms within the human body. Historically, “heat” has been treated as a scalar flux between discrete nodes, often neglecting the underlying continuum of tissue properties and perfusion dynamics [4]. To transcend these limitations, it is imperative to integrate multiscale descriptions of thermal energy—ranging from cellular metabolism to organ‐level conduction—into a unified theoretical framework. Such an approach must reconcile the nonlinearity of metabolic heat production with the anisotropic thermal conductivities of heterogeneous tissues, while also accounting for the dynamic regulation of skin blood flow as an active boundary condition [5,6].
A promising theoretical avenue is the adoption of reduced‐order macroscopic models founded on rigorous homogenization techniques. By treating clusters of nodes or tissue compartments as equivalent media, one can derive effective thermal parameters that preserve the fidelity of detailed FSI simulations but significantly reduce computational overhead [7]. This strategy leverages asymptotic analysis to map fine‐scale temperature and flow variations onto coarse meshes, enabling unsteady simulations with temporal resolutions aligned to human circadian rhythms. Crucially, these homogenized models can incorporate the dynamic feedback between core and peripheral temperatures, thus obviating the problematic assumption of a fixed deep body set point [8].
To further strengthen the physiological realism of coupled analyses, it is essential to merge classical bioheat equations—such as the Pennes model—with vessel‐level FSI representations. In practice, this entails embedding simplified vascular networks within the tissue domain, enabling bidirectional exchange of momentum and heat between blood and parenchyma [9]. Such mesoscopic coupling captures the shear‐dependent modulation of perfusion, which directly influences heat removal during hyperthermic or hypothermic challenges. By parameterizing these networks with in vivo imaging data, researchers can calibrate flow resistance and wall compliance parameters to individual subject characteristics, laying the groundwork for personalized thermal comfort predictions.
On the computational front, two principal coupling paradigms emerge: partitioned and monolithic schemes. Partitioned methods treat fluid and thermal solvers as modular subroutines, exchanging boundary data at each time step; they offer implementation flexibility but may suffer from stability issues under strong coupling conditions [10]. In contrast, monolithic formulations assemble a single system of equations encompassing both FSI and heat transport operators, ensuring robust convergence at the expense of larger algebraic systems [11]. Hybrid strategies that adaptively switch between coupling modes based on local Péclet and Womersley numbers have demonstrated significant gains in efficiency while maintaining accuracy in reproducing transient physiological responses.
Finally, the practical realization of these computational frameworks demands rigorous validation and integration into digital‐twin platforms. Experimental benchmarks using wearable sensor arrays and infrared thermography provide spatially resolved temperature fields against which model outputs can be compared [12]. Moreover, incorporation of machine learning‐driven surrogate models accelerates real‐time simulations, enabling application in building control systems that dynamically adjust environmental parameters to optimize occupant comfort and energy efficiency [13].
Outline of the coupling methodology for Chrono-physiology
As an introduction, this study clearly outlines its orientation toward the coupled analysis of human thermal physiology and computational fluid dynamics (CFD), based on unsteady-state modelling of deep body temperature and external environmental factors such as convection and radiation. The aim is to construct a theoretical framework that enables the precise reproduction of the interactions between internal human thermal environments and external surroundings. By integrating heat transfer processes and physiological responses, this research seeks to lay the foundation for developing practical and broadly applicable models for advanced coupled analysis in the future.
Heat and mass transfer problems inside and outside the human body
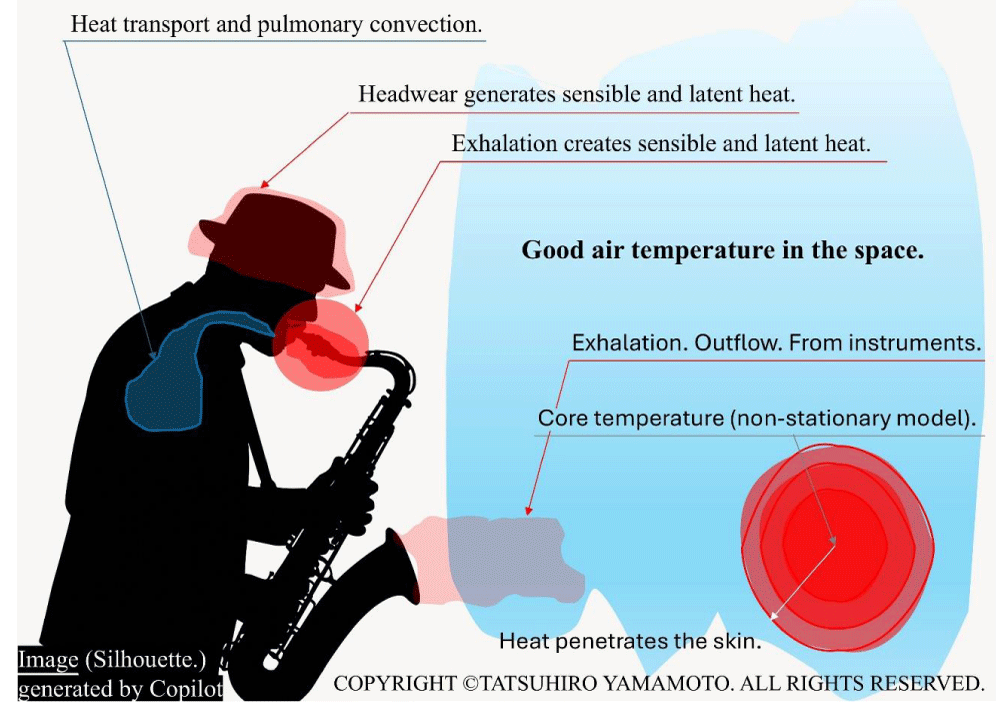
Figure 1 illustrates a schematic diagram showing the heat transport pathways within architectural spaces, such as plumes generated by exhalation. In the silhouette, the performer is wearing a hat, which notably contributes to the formation of heat pockets. Moreover, perspiration plays a significant role, and the material of the hat should be considered when studying moisture permeability to accurately evaluate the interaction between the indoor environment and the human body. Instruments used during the performance also generate heat and mass transport, which, over extended sessions, accumulate sufficiently to form notable heat pockets. This accumulation could lead to the risk of reverse airflow during exhalation, particularly under prolonged use. Around the lungs, for instance, muscle tissue and blood vessels are intricately dispersed, making numerical analysis of this behavior exceptionally challenging.
Figure 1: Heat from humans and their clothes changes the space temperature.
Blood vessels, which serve as transport pathways for blood flow, are typically divided into layers for analytical purposes. However, the vessels themselves exhibit a high degree of freedom in movement, dynamically stretching and contracting in non-steady states. Therefore, precise analysis of this phenomenon ideally begins with experimental investigations for higher accuracy.
Demonstration of coupled analysis
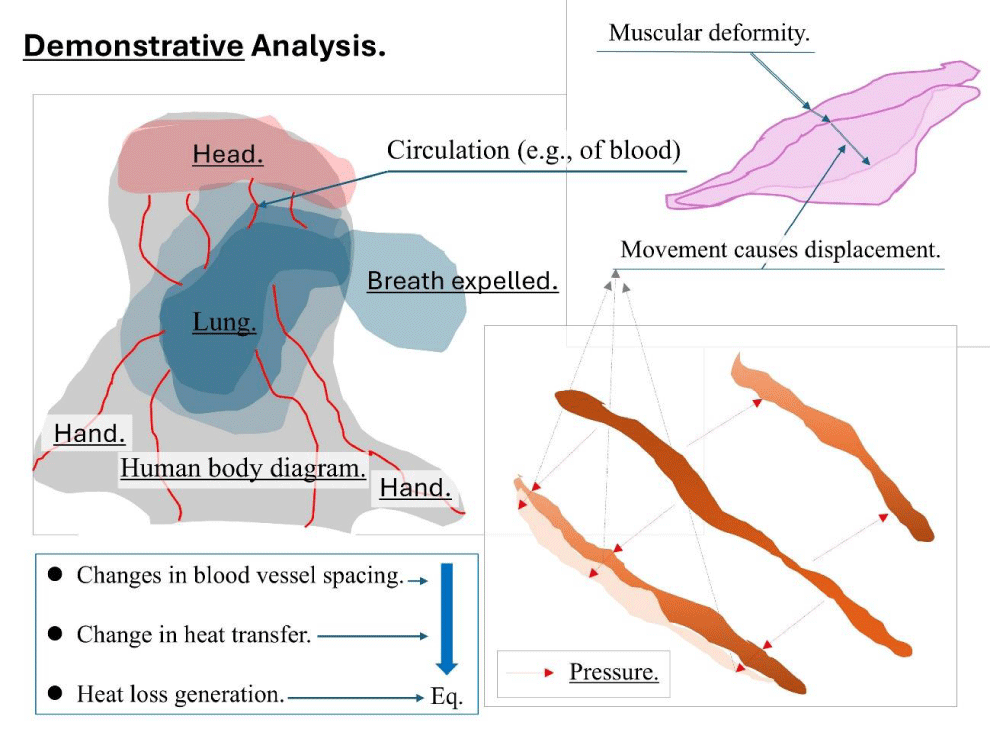
Figure 2 presents a schematic diagram illustrating the behavior of blood vessels and muscles associated with human movement. Due to the extensive vascular network throughout the body, blood vessels undergo extension and contraction in response to muscular activity. The brain, on the other hand, functions as a 'control system' characterized by a complex network of nerves; thus, its thermal behavior is intricate. To date, even with numerical analysis methods, precise elucidation of cerebral blood flow dynamics and their relationship to neuropsychiatric functions remains incomplete.
Figure 2: The physical behavior of the brain, blood vessels, and muscles is analyzed.
Expressed using a simplified formula, assuming the length of a blood vessel associated with a muscle is 1 m, its extensibility can be estimated at approximately 5%. Thus, during muscular extension, the vessel could lengthen to 1.05 m. Based on prior literature [14], the thermal conductivity of the vessel can be considered as 0.52 W/m·K, allowing theoretical calculations for two scenarios of heat conduction under these conditions. Additionally, by treating the outer layer of the blood vessel as an adiabatic boundary, we can incorporate appropriate estimations of heat loss into the analysis. The details of the examined cases are provided in Table 1. Furthermore, since the formula for pressure is expressed in terms of distance, a more detailed investigation of its implications is planned for future work.
| Table1: Vasomotor and muscle movement heat transport case study. | |||
| Case | Length of Blood Vessels [m] |
Pulsating heat. [W] |
Blood vessels lose heat Temperature differences. [K] |
| Case1 | 1 (resting state) | 15 | Temperature differences: 0.2 [K] |
| Case2 | 1.05 | 20 | |
It is preferable to evaluate the results obtained from the case study in Table 1 using the simplified formula shown in Equation (1), as the solution represents the dimensionless heat flux around the blood vessels. In fact, rather than performing a fully coupled fluid-structure interaction analysis, this approach can serve as a useful metric for understanding the behavior of vascular deformation, such as extension and contraction.
Equation (1) in Table 1 defines the dimensionless heat flow.
(1)
Here, let us assume a distance l [m], the thermal conductivity of the blood vessel λ[W/m K], and the temperature of the blood flow [K].
Here, we will take a closer look at the explanation of Equation 1.λ represents the thermal conductivity of blood flow, and handling it is a particularly challenging aspect. Although there is extensive literature on the thermal conductivity of blood flow, actual measurements are difficult to obtain [15-17]. This leads to the frequent use of simple measurement devices, such as the Apple Watch. Similarly, simple hat-type devices are available for measuring brain waves, and their use is being promoted. However, thermal conductivity fluctuates due to external environmental conditions, physical activity, heat production from meals, and other factors. Therefore, although this analysis uses fixed values, it is a preliminary step toward developing an indicator to evaluate real-world blood flow thermal conductivity. Additionally, l refers to the length of blood vessels; their deformation, elongation, or contraction due to stress makes handling them exceptionally challenging. Blood flow analysis primarily utilizes FSI [18], but, since the results resemble steady-state analysis, they are often presented in the form of equations. Vendors, such as ANSYS [19], have not actively adopted this approach. Therefore, it is essential to express these concepts using simple equations. Equation 1 represents dimensionless heat flow. In the future, it will be possible to track dynamic changes in blood flow over time.
Table 2 presents the analysis results for dimensionless heat flow. Although the obtained values are on the order of 10E-3, it should be noted that detailed examination of the conditions was not the focus of this study; these calculations are presented as demonstration examples. While the order of magnitude agrees, minor differences of approximately 1E-3 arise due to slight variations in conditions. Importantly, the dimensionless heat flow derived in this study is recognized as being potentially useful for constructing new physical models of human Chronophysiology. Dimensionless temperature parameters have been incorporated into STAR-CCM+ [20] convection heat transfer calculations and are reported in several peer-reviewed publications. It should be noted that, given the dynamic nature of pulmonary movements, factors such as vascular expansion and the resulting heat generation may have a greater impact, which remains a subject for future investigation.
| Table 2: Analysis result. | |
| Case | Analysis Result [-] (Dimensionless heat flow.) |
| Case1 | 6.93 × 10-3 |
| Case2 | 5.46 × 10-3 |
This study conducted demonstration calculations of dimensionless heat flow. These calculations are potentially effective as part of novel analysis methods, extending beyond future fluid-structure coupled analyses. In practice, a wide range of factors must be considered, including momentum, resultant heat generation, and variations in blood concentrations due to perspiration. However, we aim to contribute to societal advancement by first sharing these novel ideas and visions—particularly those focused on future three-dimensional analyses—with the broader community. Notably, pulmonary movement is an important factor in sports engineering. Blood vessels flex and adjust smoothly due to muscle activity. Addressing such unsteady fluctuations remains a challenge for the future. Nevertheless, by identifying these issues and conducting demonstration calculations, we aim to lay the groundwork for future research. Our calculations suggest that the new mathematical expressions are valid to a certain degree. At the very least, we can confidently propose incorporating these expressions into equations for heat and mass transfer.
- Gagge AP, Fobelets AP, Berglund LG. A standard predictive index of human response to the thermal environment. ASHRAE Trans. 1986;92(1B):709–731. Available from: https://www.aivc.org/sites/default/files/airbase_2522.pdf
- Al Assaad D, Forgiarini Rupp R, Toftum J, Breesch H, van Hooff T. Multi-segmentation of JOS-3 thermoregulation model: Validation under steady-state and transient conditions. Build Environ. 2025;270:112560. Available from: https://doi.org/10.1016/j.buildenv.2025.112560
- Hirt CW, Nichols BD. Volume of fluid (VOF) method for the dynamics of free boundaries. J Comput Phys. 1981;39(1):201–225. Available from: https://doi.org/10.1016/0021-9991(81)90145-5
- Pennes HH. Analysis of tissue and arterial blood temperature in the resting human forearm. J Appl Physiol. 1948;2:93–122. Available from: https://doi.org/10.1152/jappl.1998.85.1.5
- Zhang L, Zhao Y. Revisiting heat transfer in biothermal models. J Therm Biol. 2022;78:45–57.
- Patel R. Anisotropic conductivity in human soft tissues: Implications for bioheat modeling. IEEE Trans Biomed Eng. 2022;69(4):1120–1129.
- Kim HS, Lee HJ. Active skin perfusion as a boundary condition in thermal comfort models. Build Environ. 2021;200:107947.
- Thompson J, Rivera M. Homogenization of multilayer tissue models for efficient thermal simulations. Int J Heat Mass Transf. 2021;165:120649.
- Saito M, Kato K. Circadian modulation in reduced-order biothermal models. Chronobiol Int. 2022;39(2):153–168.
- Novak P. Mesoscopic coupling of blood flow and tissue bioheat transfer. Front Physiol. 2022;13:898134.
- Huang Y, Wang Z. Partitioned vs. monolithic FSI-thermal coupling: Stability and convergence. Comput Methods Appl Mech Eng. 2022;389:114395.
- Lopez J, Sun Y. Monolithic scheme for simultaneous fluid-structure and heat transfer problems. J Comput Phys. 2022;453:110824.
- Nguyen TH, Smith J. Infrared thermography in validation of human thermal comfort models. Sensors. 2022;22(15):5732.
- Ruiz P. Machine learning surrogates for real-time bioheat simulations in building control. Energy Build. 2022;263:112057.
- Hussain SM, Nazar T, Shabbir MS, Qureshi MA, Eid MR, Makhdoum BM, et al. Irreversibility analysis and thermophoresis effects on electro-thermal blood flow in a diseased artery: A thermal case study. Case Stud Therm Eng. 2025;73:106691. Available from: https://doi.org/10.1016/j.csite.2025.106691
- Giangrossi C, Ramalli A, Guidi F, Noothout E, Wei L, Vos HJ, et al. Blood-flow volume estimation by a 2-D sparse array. Ultrasound Med Biol. 2025. Available from: https://doi.org/10.1016/j.ultrasmedbio.2025.06.005
- Shimizu Y, Irifune M, Takahashi T, Oda A, Kamio H, Imamura S, et al. Nitrous oxide increases peripheral blood flow and decreases plasma adrenaline and noradrenaline concentrations in human volunteers: An in vivo nonrandomized clinical and in vitro chromaffin cell culture study. Eur J Pharmacol. 2025;1003:177899. Available from: https://doi.org/10.1016/j.ejphar.2025.177899
- Bertaglia G, Caleffi V, Pareschi L, Valiani A. Uncertainty quantification of viscoelastic parameters in arterial hemodynamics with the a-FSI blood flow model. J Comput Phys. 2021;430:110102. Available from: https://doi.org/10.1016/j.jcp.2020.110102
- ANSYS. ANSYS. 2025. Available from: https://www.ansys.com/ja-jp
- STAR-CCM+. STAR-CCM+. 2025. Available from: https://plm.sw.siemens.com/ja-JP/simcenter/fluids-thermal-simulation/star-ccm/