More Information
Submitted: January 19, 2025 | Approved: January 23, 2026 | Published: January 26, 2026
How to cite this article: Bhandari PN, Bhandari NM. Unification of Gravitational Law across the Universe is the Confirmation of an External Energy Source. Int J Phys Res Appl. 2026; 9(1): 012-023. Available from:
https://dx.doi.org/10.29328/journal.ijpra.1001142
DOI: 10.29328/journal.ijpra.1001142
Copyright license: © 2026 Bhandari PN, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is propeRLy cited.
Keywords: Dx factor; Inertia factor; Geometric law; Black hole singularity
Unification of Gravitational Law across the Universe is the Confirmation of an External Energy Source
Pushpak N Bhandari1 and Nandan M Bhandari2
1PhD, Purdue University, USA
2MSc, University of Saskatchewan, Canada
*Address for Correspondence: Nandan M Bhandari, MSc, University of Saskatchewan, Canada, Email: [email protected]
A novel theory of Quantum Gravity is proposed, asserting that the Universe’s fundamental forces are driven by external energy originating from the Space and Time Dimensions. The framework introduces Space-Time Quanta as the universe’s fundamental building blocks. Gravitational force is posited to arise from an energy shadow or energy deficiency between objects, replacing the conventional spacetime curvature model.
The core achievement is the Unified Mass-Inertia Force Equation, which decomposes the force into two factors:
- Mass Factor M = MCS1 X MCS2: Associated with the Time Dimension, this factor dominates macroscopic gravity.
- Inertia Factor I = 1/ Dx^2: Associated with the Space Dimension, this factor governs microscopic interactions.
Resulting in: Gravitational Force = K*M*I
where K = 63.87×G; M = MCS1×MCS2; I = 1/(Dx)2
This unified model successfully validates all the regimes:
- Quantum scale: The geometric contraction of the Dx factor models quark confinement, mathematically replacing the characteristic 1/R2 dependence at short range and the exponential force increase required for hadronisation.
- Cosmological scale: The theory defines a Black Hole geometrically: The Singularity is defined as the resulting point of maximal energy consumption.
- Visible scale: Dx, the factor or inertia factor is the diameter of the energy shadow cone that controls the Gravity between two objects [1,2].
This work provides a mathematically robust, geometric alternative to current field theories, supporting the evolution of the Universe through external energy and its propagation by multiplication of Space-Time Quanta.
PACS Nos.: 04.70.-s; 12.38.-t; 02.40.-k, 12.10.-g
- PACS Nos.: 04.70.-s (Physics of black holes)
- PACS Nos.: 12.38.-t (Quantum chromodynamics/Quarks)
- PACS Nos.: 02.40.-k (Geometry, differential geometry, and topology)
- PACS Nos.: 12.10.-g (Unified theories and models)
Understanding the fundamental origin of gravitational and strong nuclear forces remains a central challenge in modern physics. General Relativity (GR) describes gravity as curvature of a continuous spacetime, whereas Quantum Chromodynamics (QCD) models confinement using gluon flux tubes and asymptotic freedom. These theories operate successfully within their regimes, yet they lack a unifying conceptual basis and differ in their treatment of space, time, and mass.
In this paper, we explore the hypothesis that the Universe is driven by a constant inflow of external energy from orthogonal Space and Time dimensions. Material bodies partially obstruct this influx, creating “energy-shadow regions.” The interaction between such shadows gives rise to forces that can be described at both macroscopic and quantum scales.
By modelling these energy shadows as intersecting spheres, we derive the diameter of their intersection 𝐷x. Analytically, show that the force between bodies is naturally proportional to 1/(𝐷x2). This formulation reproduces Newtonian gravity for astronomical bodies while predicting confinement behaviour at femtometer scales, physics at the black hole level, and the behaviour of objects entering black holes.
Limitations of curvature-based gravity
General Relativity has no built-in microscopic mechanism for inertia or gravitational force. Mass–energy curves spacetime, but the origin of inertia and the reason bodies resist acceleration are not fundamentally explained.
Limitations of QCD confinement
QCD explains confinement through gluon self-interactions, which give rise to a string tension. However:
- The value of σ, string tension, is empirical;
- Confinement is modelled by potential forms rather than direct geometric necessity;
- Gluon string breaking is a phenomenological insertion, not a geometric prediction.
Need for a geometric, parameter-free force law
A geometric force law valid at all scales eliminates:
- Arbitrary fitting constants,
- Region-specific phenomenology,
- Conceptual discontinuity between strong and gravitational interactions.
This motivates a unified alternative.
We assume that the Universe receives a continuous energy inflow from external orthogonal dimensions (“Space” and “Time”), composed of discrete quanta too small to be detected individually [2].
Matter as an obstruction
A mass 𝑀 Partially blocks this inflow, forming a spherical energy-shadow region around it. The shadow has:
- An effective radius related to the mass,
- A deficit of incoming energy relative to free space,
- Resulting inward pressure.
Dx and interaction of energy shadows leading to gravitational force
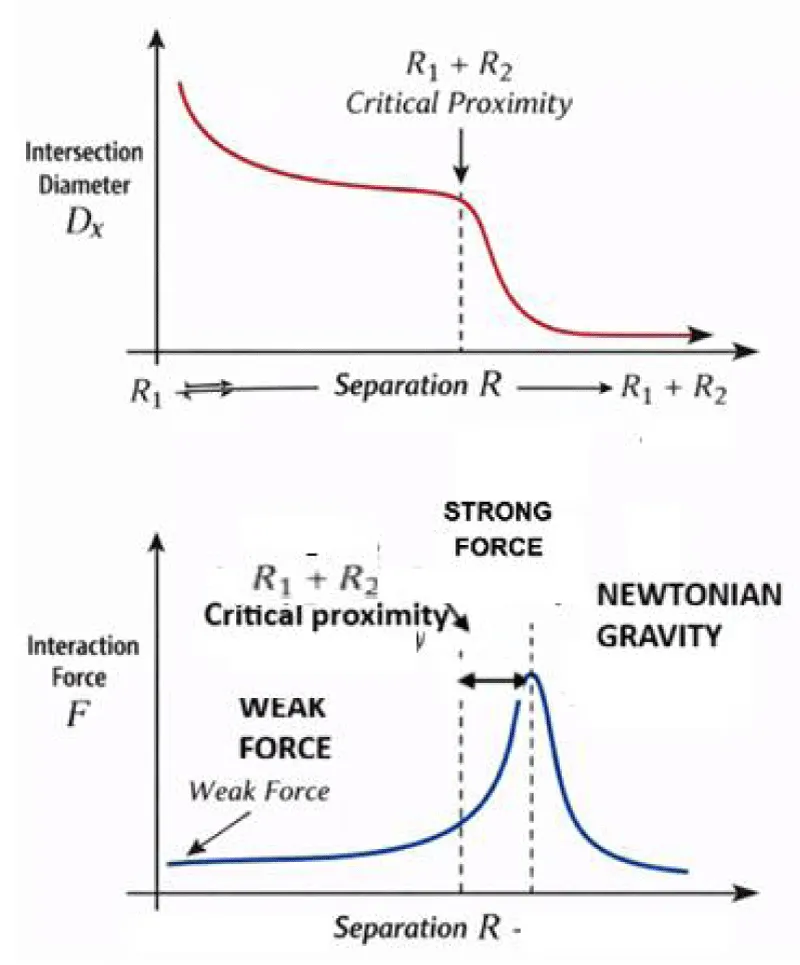
When two shadow spheres overlap, their intersection region produces a force. The intersection diameter measures the size of this overlap. The force law becomes fundamentally inversely proportional to Dx2.
Detailed discussion: The authors [1,2] proposed a theory stating that the Universe derives its energy from the External O-Dimensions, which were later renamed the Space Dimension and the Time Dimension [2]. The Gravitational Force between two objects was proposed by virtue of the formation of an energy shadow between the two objects. The gravitational force equation [1-4] was derived from this principle, and the values obtained using the new equation matched well with Newtonian values [1,2]. As this work continues the author’s earlier work [1,2], it is recommended that the earlier work be read as well.
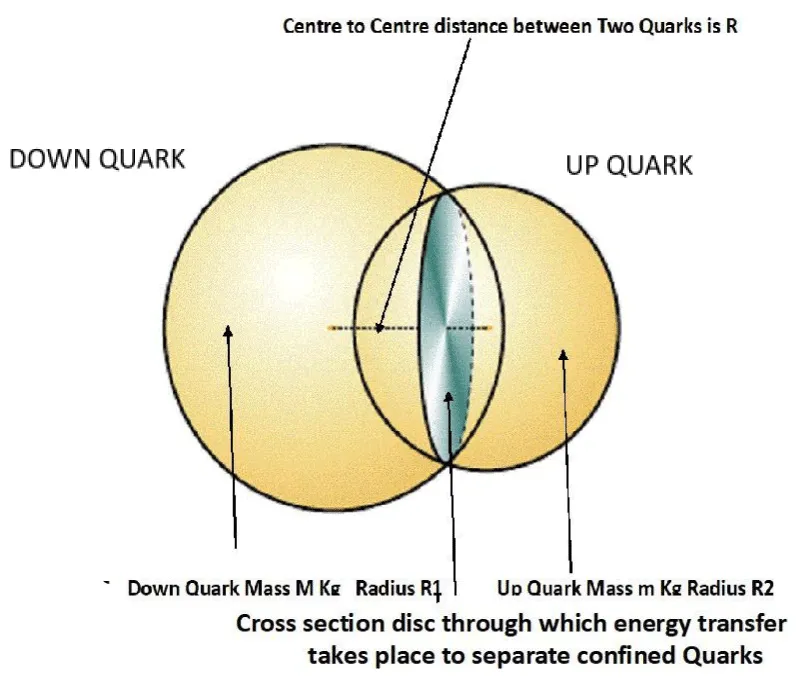
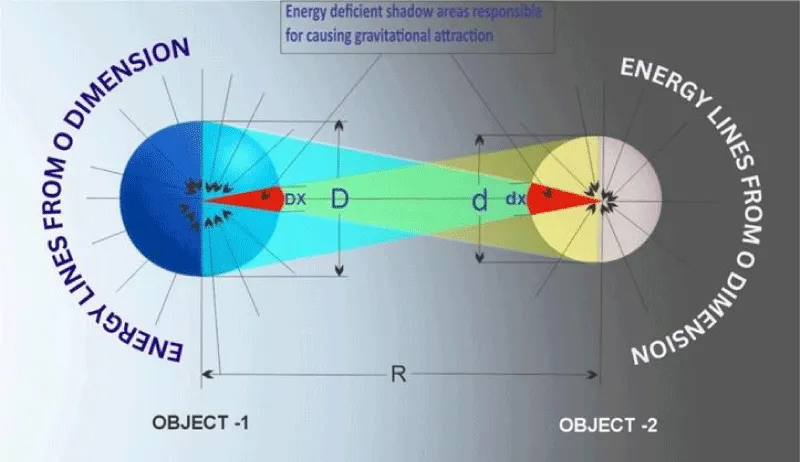
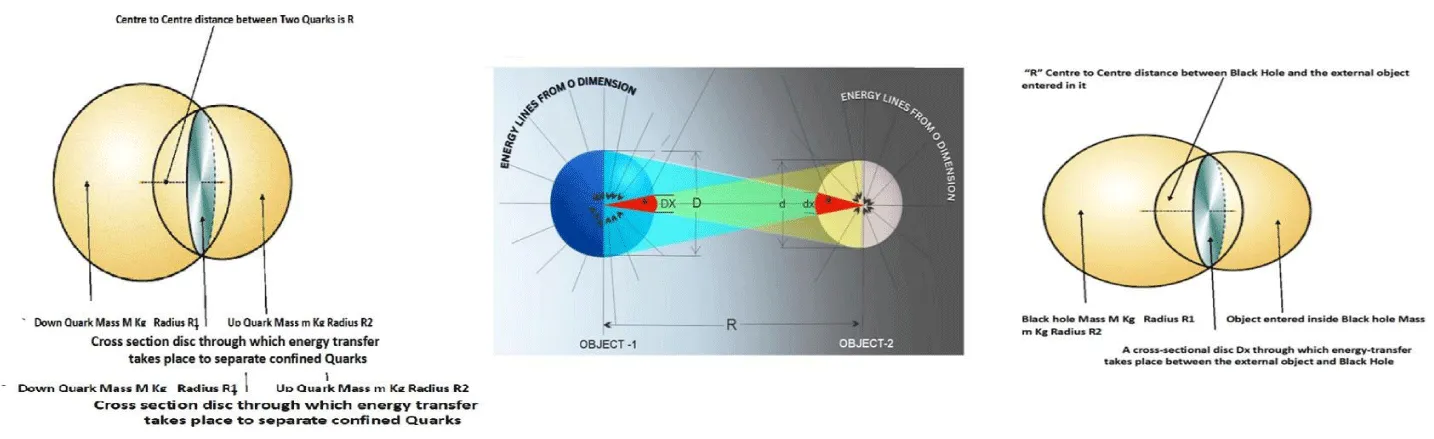
Figure 1 illustrates the formation energy shadows cast by two objects on each other, which leads to the creation of the Gravitational Force between them. MCS1 and MCS2 are the sections of the objects having an energy deficiency. R is the distance between the centres of two objects, and Dx and dx are the diameters of energy-starved cones.
Figure 1: Objects receiving energy from external sources cast energy shadows on each other, giving rise to a Gravitational Force between them.
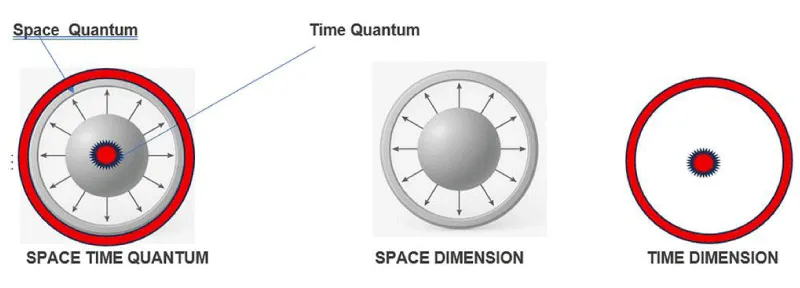
Authors [2] proposed the space–time quanta as a fundamental building block of the Universe. The concept of Special relativity could be well visualised with these concepts, and it provides a new perspective on wave-particle duality, the double-slit experiment, and quantum entanglement. It re-examines the principles of Special Relativity, offering a conceptual and visual explanation of phenomena such as time dilation and length contraction as consequences of changes in the Space-Time quanta [2]. The theory also provides an alternative view of the origin of the universe and the nature of gravity, suggesting that gravitational effects arise from an energy deficiency rather than from spacetime curvature. This paper establishes a conceptual foundation for further mathematical development to test and validate these new insights.
The gravitational force equation, which has been arrived at, is:
Gravitational Force = 63.83×G×MCS1×MCS2/(Dx)2 [1-3] (1)
Where:
- MCS1 is the mass of the shadow cone of Object 1, which is starved for energy (Unit kg)
- MCS2 is the mass of the shadow cone of Object 2, which is starved for energy (Unit kg). It is assumed that MCS1 > MCS2.
- C = Velocity of light = 3 × 108 m/s
- R = Shortest distance between two objects
Here, G is the universal gravitational constant: 6.743 × 10−11 m3 kg−1 s−2. Geometrically Dx = dx.
The product of masses of two objects in Newton's equation is replaced by the product of the Conical sections of the energy-deficient sections of two objects. We call this factor the Mass factor “M”. M= MCS1×MCS2.
This product of the energy-deficient masses is further multiplied by a factor “1/ (Dx)^2“
We call this the Inertia factor “I”. I = 1/(Dx)2 Thus,
Gravitational Force = K*M* (2)
where K = 63.87 × G; M = MCS1 × MCS2; I = 1/(Dx)2
Mass factor M represent the energy source from the Time dimension, and Inertia factor I represents energy from the Space dimension.
The “M” fraction of the gravitational force equation makes a significant contribution to the force for large objects like planets, etc. Still, the Inertia fraction becomes dominant when calculating the force between microscopic objects, such as quarks, and in the behaviour of objects near black holes.
The attractive force between two quarks increases as you increase the distance R between two quarks. As R increases, Dx decreases, and the Inertia factor “I” increases. This is consistent with the behaviour of quarks, which exhibit an increasing attractive force, like rubber bands, as they are stretched further.
Comparison between new gravitational force equation and Newton’s equation:
Newton’s equation:
Gravitational force = G × M1 × M2/R^2 (3)
(M1 and M2 represent the total mass of two objects, and R is the centre-to-centre distance between two objects)
New proposed equation:
Gravitational force = 63.83 × G × MCS1 × MCS2/(Dx)2.
(MCS1 AND MCS2 are the Masses of conical energy-deficient sections of the objects, and Dx is the base diameter of the energy-deficient fractions). It is possible to introduce the fine-structure constant in this equation (1/α = 137.035999177). So 1/(2 α) = 68.518. It is hypothesised that the fundamental constant Cunified = 63.832 represents a deep geometric analogue to the fine-structure constant α. If a quantum correspondence is assumed, the unified force equation suggests a direct relationship to electromagnetism:
F α (1/(2 α)) *G*M*I . (4)
F *G*M*I (5)
Where (1/(2 α)) = 68.518. The small numerical difference between the derived value 63.832 and the quantum value 68.518 can be viewed as the residual geometric contribution necessary for the gravitational coupling."
This correspondence with α is the first step toward a Geometric Grand Unified Theory (GUT), connecting Mass-Inertia Gravity (which handles confinement) to QED (Electromagnetism).
Current theory proposes external energy sources from two origins; hence, in the new equation, the fraction “M” (MCS1 × MCS2) has a significant contribution from the Time-dimension energy source when objects are Macroscopic. In contrast, when the objects are microscopic of a quantum nature, the “I”, 1/(Dx)2 gives a significant contribution to the total energy having origin from the space dimension.
Energy-deficient cone diameter Dx is dependent on R, the centre-to-centre distance between the objects and the object's size. For instance: "Unlike the fixed distance 'R' in Newton's law, the diameter of the energy-deficient section, 'Dx', changes based on the size of the objects and their separation 'R', linking the geometry of the energy shadow directly to the resultant force."
This factor decomposition is central to the theory: the Mass factor “M”, derived from MCS1 * MCS2, represents the contribution of energy from the Time dimension and primarily governs macroscopic interactions. Conversely, the Inertia factor “I” (1/(Dx)^2) captures the energy contribution from the Space dimension, becoming dominant in quantum-scale interactions like those between quarks.
It was decided to apply the external energy source, the Gravitational model, to quarks and check the results to see if they match the observations.
Gravitational equation used for Planets, wherein Force is proportional to the shadows cast by planets on each other and inversely proportional to the square of the diameter of the aperture through which the energy flows:
Gravitational Force = 2×7.978975×G×MCS1×MCS2/(Dx/2)^2
In this quark section, we have taken MCS1 = M and MCS2 = m
Or
Gravitational Force = 63.8318×G×M×m/(Dx)^2 Mass Factor “M” = M×m
At a quantum level, two quarks are in a composite state, and there is no distinct separation between them. Hence, the shadow on a larger quark is equal to the volume of a small quark; hence, assuming both quarks of the same density, M is taken as equal to m.
Hence, Mass Factor M = m2
Inertia Factor “I” = 1/Dx^2
Gravitational force is the product of mass factor and inertia factor,
F = 63.8318 x G x M x I
Quark properties:
A pair of up and down quarks is used to verify the model.
The literature does not provide consistent values for quark properties such as mass and radius. Hence, the literature is used to derive average representative values to validate the proposed theory.
Two different quark sizes were used to verify the model, and their approximate values were also taken into account. These approximate values are derived from diverse data in the literature [5-8].
Two models are used for validation purposes as follows:
Model 1: Radius of Up Quark: 2.14 * 10^ -34 meter and Down quark 4.27* 10^-34 meter; Mass of Up Quark: 3.9218*10^-30 Kg and Down quark 8.38*10^-30 Kg
Model 2: Radius of Up Quark: 2.136 * 10^ -25 meter and Down quark 4.27* 10^-25 meter; Mass of Up Quark: 3.9218*10^-30 Kg and Down quark 8.38*10^-30 Kg
Confinement: Owing to a phenomenon known as colour confinement, quarks are never found in isolation; they can be found only within hadrons, which include baryons (such as protons and neutrons) and mesons, or in quark–gluon plasmas. For this reason, much of what is known about quarks has been drawn from observations of hadrons [6]. It is impossible to separate quarks as they always exist in a composite or superposition form, such that the force required to isolate them increases as they are stretched. As the stretch distance increases, the force required increases exponentially.
Geometric confinement via contraction. As the centre-to-centre distance between two quarks increases, the diameter of their intersection (Dx) decreases. This geometric reduction causes the Inertia Factor 1 to grow exponentially, leading to an exponential rise in confinement force, thereby confirming the impossibility of isolation.
In the current theory, the Inertia factor is a controlling factor rather than the string tension in conventional Quantum Chromodynamics. The inertia factor is the reciprocal of the square of the radius of the intersection circle of two quarks, as illustrated in Figure 1. In QCD, the string connecting quarks gets stretched. In contrast, in the current theory, the diameter of the quark-quark intersection decreases with increasing separation. At the centre-to-centre distance equal to the sum of the radii of two quarks, the cross-sectional area of the intersection of two quarks reaches zero, leading to the Inertia factor increasing, causing the interaction force to diverge geometrically beyond any finite opposing force. Subsequently, the force required for separation becomes unachievable, confirming that it is impossible to separate the two quarks.
Below are the results of the Calculation of the Force required to pull the quark to attempt to isolate it. Mass of the bigger quark is taken as “M”, and that of the smaller quark is taken as “m” Kg. The model represented by equation 2 accounts for the energy shadows cast by the objects under consideration. In the case of quarks, both quarks are in the amalgamated state, and they cast a shadow on each other equivalent to the mass of the smaller quark “m”. Hence, for the calculation of the quark force equation 2 transforms into:
Gravitational Force = 63.832×G×m^2/(Dx)^2
m is the mass of the smaller quark. Dx is the diameter of the intersecting disc between two quarks, illustrated in Figure 2.
Figure 2: The Fundamental building block of the universe is defined as a SPACE-TIME* quantum, which is a superposition of space and time* quanta.
Equation for the calculation of Dx is:
(6)
Above equation is derived using the geometry of the intersection of quarks.
Distance from centre to intersection plane
Using the standard sphere–sphere intersection geometry:
Intersectional Radius
Dx = 2𝑟
Which can also be written as:
(7)
Intersection occurs only when:
∣R1 – R2∣≤𝑅≤R1 + R2.
When 𝑅 = 𝑅1 + 𝑅2 or 𝑅 = ∣𝑅1 − 𝑅2∣, we have 𝐷x = 0.
R1 is the Radius of the Down Quark; R2 is the Radius of the up quark; R is the centre-to-centre distance between the two quarks.
Model 1 (Smaller Diameter Quarks) (Figures 4,5) (Tables 1-4)
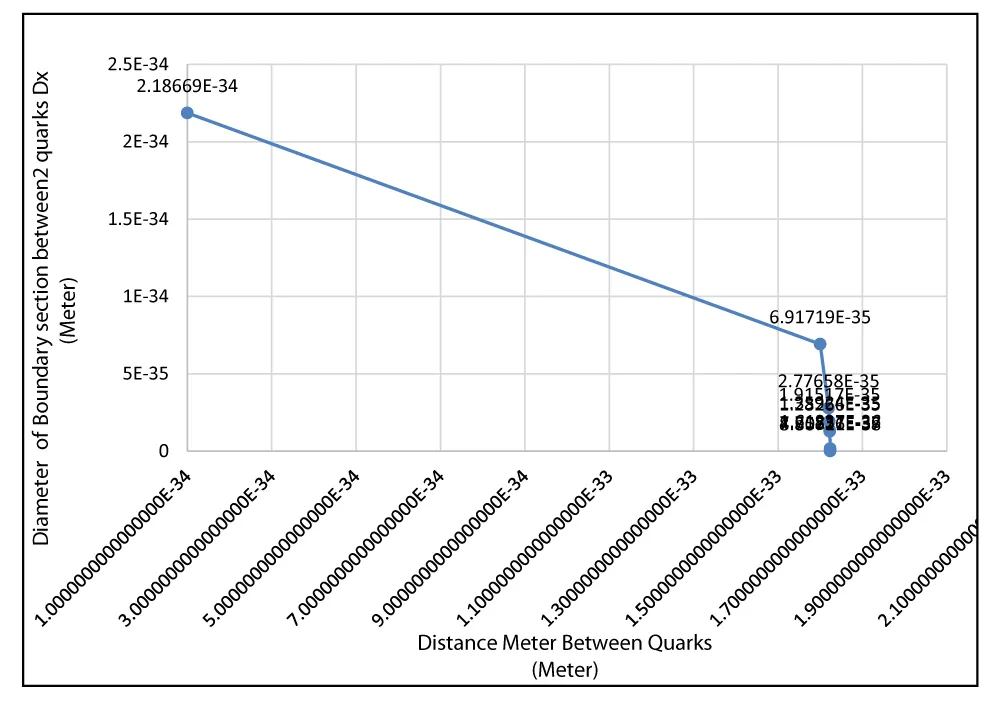
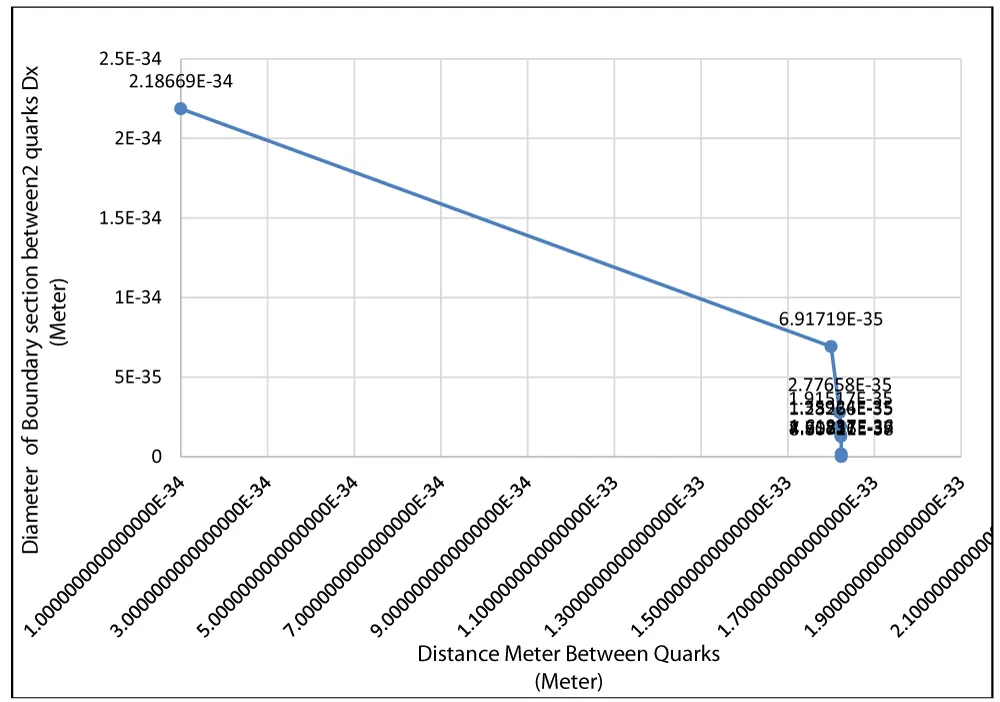
Figure 4: (Small diameter quark model) As the distance between Quarks,R, crosses the critical value intersection diameter Dx, it drops sharply.
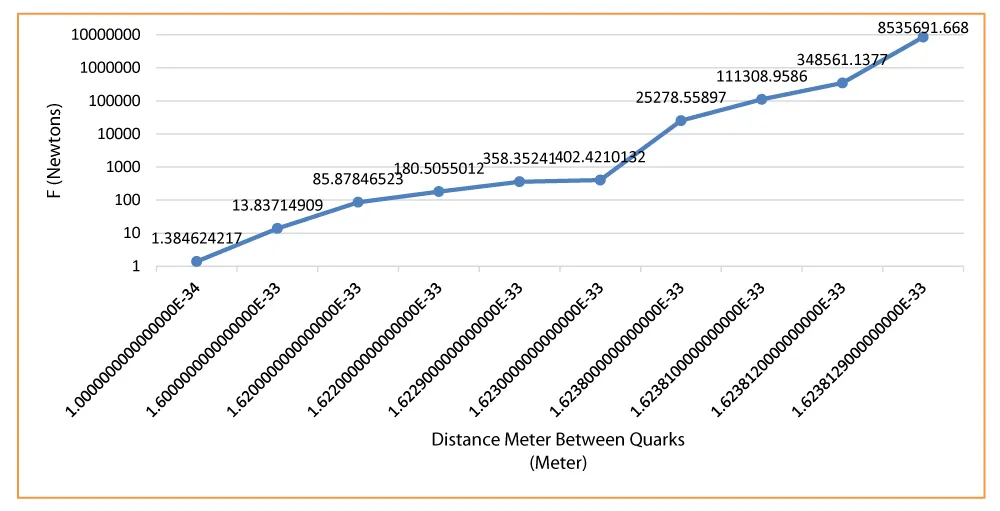
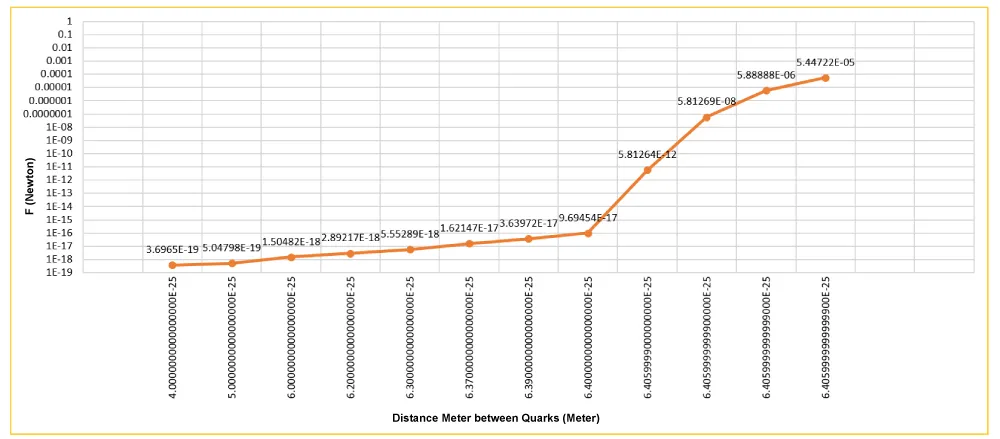
Figure 5: Exponential rise in confinement force between quarks as the intersection diameter is reduced below the critical level for small diameter model.
| Table 1: Calculation of Dx, intersection Diameter for the values of R, distance between 2 quarks (Small diameter quarks). | |
| x axis | y axis |
| Distance Meter Between Quarks (Meter) | Diameter of Boundary section between2 quarks Dx (Meter) |
| 2.18669E-34 | 1.0000000000000000E-34 |
| 6.91719E-35 | 1.6000000000000000E-33 |
| 2.77658E-35 | 1.6200000000000000E-33 |
| 1.91517E-35 | 1.6220000000000000E-33 |
| 1.35924E-35 | 1.6229000000000000E-33 |
| 1.28266E-35 | 1.6230000000000000E-33 |
| 1.61837E-36 | 1.6238000000000000E-33 |
| 7.71237E-37 | 1.6238100000000000E-33 |
| 4.35826E-37 | 1.6238120000000000E-33 |
| 8.80711E-38 | 1.6238129000000000E-33 |
| Table 2: Confinement Force Calculations as a function of Intersection diameter for small diameter quark model. | |
| y axis | x axis |
| F = 2*7.978975*G*m^2/(Dx/2)^2 (Newton ) |
Distance Meter Between Quarks (Meter) |
| 1.384624217 | 1.0000000000000000E-34 |
| 13.83714909 | 1.6000000000000000E-33 |
| 85.87846523 | 1.6200000000000000E-33 |
| 180.5055012 | 1.6220000000000000E-33 |
| 358.35241 | 1.6229000000000000E-33 |
| 402.4210132 | 1.6230000000000000E-33 |
| 25278.55897 | 1.6238000000000000E-33 |
| 111308.9586 | 1.6238100000000000E-33 |
| 348561.1377 | 1.6238120000000000E-33 |
| 8535691.668 | 1.6238129000000000E-33 |
| Table 3: (Larger diameter quarks) Calculation of Dx, intersection Diameter for the values of R, distance between 2 quarks (Larger diameter quarks). | |
| Distance Meter Between Quarks R, meter | Intersection Diameter Dx, meter |
| 4.0000000000000000E-25 | 4.23211E-25 |
| 5.0000000000000000E-25 | 3.62155E-25 |
| 6.0000000000000000E-25 | 2.09754E-25 |
| 6.2000000000000000E-25 | 1.51301E-25 |
| 6.3000000000000000E-25 | 1.09193E-25 |
| 6.3700000000000000E-25 | 6.38997E-26 |
| 6.3900000000000000E-25 | 4.265E-26 |
| 6.4000000000000000E-25 | 2.6133E-26 |
| 6.4059999000000000E-25 | 1.06725E-28 |
| 6.4059999999900000E-25 | 1.06725E-30 |
| 6.4059999999999000E-25 | 1.06032E-31 |
| 6.4059999999999900E-25 | 3.48631E-32 |
| Table 4: Confinement Force Calculations as a function of Intersection diameter for largerl diameter quark model. | |
| Distance Meter Between Quarks meter | F = 2*7.978975*G*m^2/(Dx/2)^2 Newtons |
| 4.0000000000000000E-25 | 3.6965E-19 |
| 5.0000000000000000E-25 | 5.04798E-19 |
| 6.0000000000000000E-25 | 1.50482E-18 |
| 6.2000000000000000E-25 | 2.89217E-18 |
| 6.3000000000000000E-25 | 5.55289E-18 |
| 6.3700000000000000E-25 | 1.62147E-17 |
| 6.3900000000000000E-25 | 3.63972E-17 |
| 6.4000000000000000E-25 | 9.69454E-17 |
| 6.4059999000000000E-25 | 5.81264E-12 |
| 6.4059999999900000E-25 | 5.81269E-08 |
| 6.4059999999999000E-25 | 5.88888E-06 |
| 6.4059999999999900E-25 | 5.44722E-05 |
Results of the calculations are as follows:
| UP QUARK Mass (Kg) | 3.92184*1^ -30 | Radius 2.14 * 10^ -34 (Meter) |
| Down quark Mass (Kg) | 8.30E*10^-30 | Radius 4.27* 10^-34 (Meter) |
As the R distance between centres of the two quarks crosses R (critical), the force required to break confinement increases exponentially.
Two graphs show the decrease in energy transition cross-section diameter between two quarks and the increase in force required as we separate them from each other. This model takes into account quarks with a radius of the order of 10^-34 meters. At R value of 6.405995*10^-34 the force required reached 10^5 Newtons (Figure 3).
Figure 3: Two quarks in a confined state and getting stretched away by an external force.
Model 2 (Bigger Diameter Quarks)
As the R distance between centres of the two quarks crosses R (critical), the Dx value falls sharply.
As the R distance between centres of the two quarks crosses R (critical), the force required to break confinement increases exponentially.
Figure 6 shows the data generated using the proposed MASS INERTA equation for Model 1 mentioned above. In Model 1, Quark sizes are approximately 10^-34 meters. As the distance between two quarks increases and reaches the sum of the radii of the two quarks, the inertia factor grows without bound, rendering any finite escape energy insufficient. At an R value of 6.405995*10^-34, the force required reached 10^5 Newtons.
Figure 6: As the distance between Quarks,R, crosses the critical value intersection diameter Dx, it drops sharply. (larger diameter quark model).
Figure 7 shows the data generated using a larger order size of 10^-25 meters. Behaviour is similar, and the separation force required reaches an extreme impossible to achieve value as the distance between two quarks reaches to the sum of the radii of the two quarks. At R value of 6.405999999999999999999999999999 *10^-34 meter (slightly less than R1+R2) the force required reached 10^5 Newtons.
Figure 7: Exponential rise in confinement force between quarks as the intersection diameter is reduced below the critical level for the larger diameter model.
Mathematical analysis of the confinement force confirms that it is impossible to isolate two quarks from each other, as the force required to separate them diverges when they are stretched apart.
Hadronisation: The force required for confinement breaking or Hadronisation as a function of the distance between the quarks was calculated and plotted. In Model 1, Quarks of smaller diameters are used, whereas in Model 2, quarks of a larger size are used for analysis. In Model 1, the quark radius of the order 10^-34 meter is used, whereas in MODEL 2, the quark radius of the order 10^-25 meter is used. As the distance between two quarks increases, the intersection diameter through which the hadronisation force acts decreases. At one stage, when (R1+R2)-R falls below 10-7*(R1+R2), there is a steep decrease in intersection diameter and a sharp increase in the hadronisation force. We call the distance R when (R1 + R2)- R < 10-7*(R1+R2)) the critical distance R(critical). Beyond this point, the minimal force required for hadronisation is transmitted, crossing Dx, the intersection of the two quarks. Almost all energy added after a distance R(critical) between two quarks results in direct addition in the quarks, which results in increasing the energy and size of the quarks. When energy added is beyond the energy that the quarks can sustain, the cleavage of quarks takes place, and a new pair of quarks (mesons) is formed. This behaviour is analogous to the propagation of space-time quanta during the formation of the Universe [2], with energy supplied by the Space and Time dimensions, according to current theory.
The Above Figures show that, according to current theory, as the distance between two quarks exceeds R(critical), the force transmission through the quark-quark intersection is minimal, and the force increases the sizes of the quarks and their energies. When the energies of quarks exceed the confinement energy of space, quarks are cleaved, and a new pair of quarks is formed.
When the separation distance exceeds R(crit), the external force no longer transmits effectively through (Dx). The excess energy directly increases the size and energy of the original quarks. This energy addition ultimately causes the highly energised quarks to cleave, generating the new quark-antiquark pair, a mechanism argued to be more logical than the breaking of a highly stretched string.
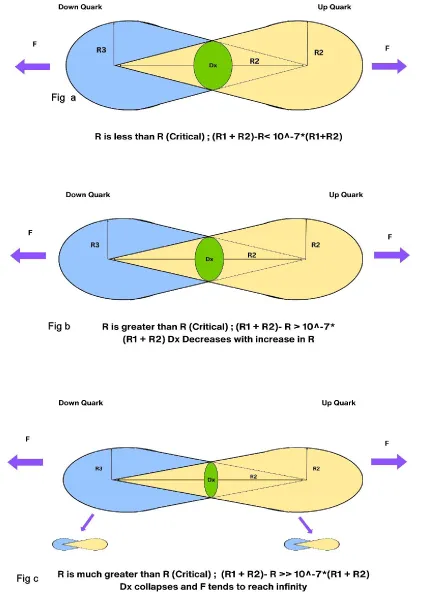
Macroscopic Dominance. For large objects, the Mass Factor (M) associated with the Time Dimension provides a significant contribution to the force. The geometry of the Inertia factor Dx is secondary (Figure 8a).
Quantum Dominance. For microscopic objects, the Inertia Factor (I) associated with the Space Dimension governs the interaction. The force is determined by the shrinking intersection diameter Dx(Figure 8b & 8c).
Figure 8: Three stages of quark-hadronisation: As R, the distance between quarks gets stretched, Dx decreases.
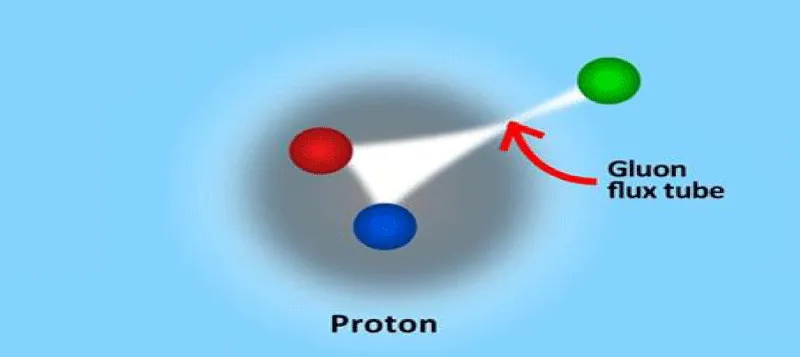
Figure 9 shows the behaviour of quarks according to quantum chromodynamics. Here, the added force produces a flux tube or flux string that is stretched by nearly 1020 times the quark diameter before breaking and the formation of new quarks. Hadronisation behaviour is better visualised in current theory than in quantum chromodynamics.
Figure 9: (Hadronisation according to Quantum Chromodynamics.
Comparison with quantum chromodynamics (Table 5)
Table 5: Comparison of the current theory with quantum chromodynamics. |
|
| Present Theory | Quantum Chromodynamics |
| The MASS-INERTIA equation governs the confinement force | Confinement is explained by String tension |
| As quarks are separated, the diameter of the intersection between two quarks, “Dx”, gets reduced |
As quarks are separated, the string connecting two quarks gets stretched, and energy is stored in the stretched string |
| Dx is explained geometrically without any ambiguity | String is stretched almost 10^20 times the diameter of quarks, which does appear logical |
| Quarks increase in size with increasing energy and then decay. Formation of a new quark from a high-energy quark is more logical. |
The string gets stretched with additional energy and then breaks. Breaking a this string to form a new Quark sounds less logical. |
Application of this theory to black holes
The success of the Dx2 Inertia Factor in modelling the force-divergence characteristic of quark confinement suggests the same geometric principle must define the ultimate force threshold in the macroscopic universe: the Black Hole Event Horizon.
The laws of Physics have been considered violated at Black Holes. However, current theory places black holes within the Domain of Physics. Any object that enters a Black hole cannot escape. The model developed for quantum gravity applies well to Black holes and explains their physics.
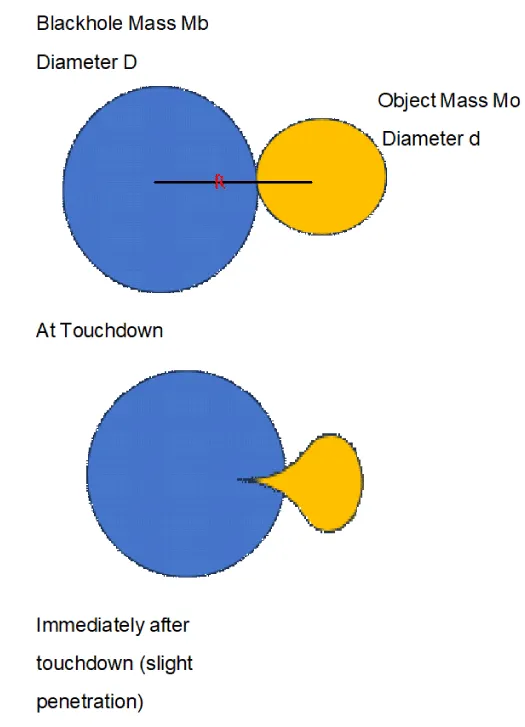
Black Hole Behaviour (Figure 10)
Figure 10: Black Hole Behaviour.
Force = C * G* M*I
Before touchdown F = C *G*M*I
Mass Factor M = Mb * Mo Inertia Factor I = 1/Dx^2 Before Touchdown Dx < d/2 At touchdown Dx = d/2
Slight penetration in Black Hole Dx ≈ 0
In the present framework, the classical event horizon is replaced by a geometric capture condition defined by the collapse of the intersection diameter Dx. The Schwarzschild radius emerges as an effective scale at which Dx approaches zero for infalling matter, rather than as a fundamental causal boundary.
Consider a black hole of mass Mb and an object of mass Mo, each associated with an Energy-shadow region of effective diameter. The interaction force is given by
Force = C * G* Mbs*Mos/Dx2 (8)
Mbs Mass of shadow region on black hole, and Mbo = Mass of shadow region on object
Where Dx is the intersection diameter between the two shadow regions, the shadow of a black hole has the volume of the object entering it, but with the black hole's density. So, Mbs is the product of the object's volume and the black hole's density.
Before contact, the deflection angle decreases as the object approaches the black hole. At the point where 𝐷x becomes comparable to the object’s effective diameter, the inertia factor increases sharply. Upon slight penetration, 𝐷x collapses toward zero, causing the interaction force to diverge beyond any finite bound.
As a result, the object is unavoidably captured. Once inside the black hole, escape would require overcoming a force that diverges geometrically, rendering escape physically impossible within this framework (Table 6).
| Table 6: Force behaviour for the object entering a black hole. | |||
| Phase | Geometric Condition | Force Behavior | Result |
| Approach | Dx < d/2 | Dx decreases as the object approaches | The Inertia Factor (I) increases sharply as the object's effective diameter approaches the object's diameter. |
| Touchdown | Dx=d/2 | Marks the geometric boundary of initial contact | The force has reached a maximum finite value defined by the geometry |
| Penetration | Dx→ 0 | Dx Collapses toward zero, and Force increases exponentially. | The interaction force geometrically diverges beyond any finite bound F→ ∞, rendering escape physically impossible. |
Extension to astrophysical scales: Black hole behaviour
The geometric mechanism underlying the mass–inertia force law is scale-independent and therefore applies equally to microscopic confinement and macroscopic gravitational collapse. In the preceding sections, it was shown that the divergence of the inertia factor provides a natural explanation for quark confinement without invoking string tension. In this section, the same geometric principle is extended to the strongest known gravitational systems—black holes.
Geometric interpretation of black hole capture
The success of the , the inertia factor in modelling force divergence at the quantum scale, suggests that the exact geometric mechanism governs black hole capture. In the present framework, black holes are not defined fundamentally by spacetime curvature singularities or event horizons, but by a geometric interaction condition arising from the collapse of the intersection diameter Dx between energy-shadow regions.
Consider a black hole of mass Mb and an infalling object of mass Mo, each associated with an effective energy-shadow domain. The interaction force between them is given by
where Mbs and Mos represent the masses of the energy-deficient shadow regions of the black hole and the object, respectively, and Dx is the diameter of their geometric intersection. In this formulation, the shadow region of the black hole has a volume scale comparable to that of the infalling object while retaining the black hole's density profile, leading to dominance of the mass factor.
As the object approaches the black hole, Dx follows the behaviour according to the equation Dx = 2*(R1*R2) / R, where R is the centre-to-centre distance between the black hole and the object, R1 is the radius of the black hole, and R2 is the radius of the object.
Upon slight penetration beyond the critical capture boundary, the intersection diameter collapses toward zero when Dx is governed by the equation:
At the point of penetration, the Black hole and the object cease to be separate entities and behave differently from before touchdown. The new formula for Dx becomes applicable at this point. This geometric collapse causes the force to diverge beyond any finite opposing interaction, thereby rendering capture inevitable.
Escape from a black hole is therefore prohibited not by causal disconnection or infinite spacetime curvature, but by geometric inevitability. As Dx → 0, the inertia factor grows without bound, rendering any finite escape energy insufficient. In this interpretation, the Schwarzschild radius emerges as an effective geometric threshold at which the collapse of Dx becomes unavoidable, rather than as a fundamental boundary of spacetime itself.
Absence of physical singularities
A significant consequence of this geometric interpretation is the elimination of physical singularities. Because the divergence of force arises from the collapse of a finite geometric quantity rather than from divergent mass density or curvature, the present framework replaces classical singularities with finite-size, ultra-dense stable cores. Physical infinities are avoided, while all observable black hole behaviours—irreversible capture, extreme gravitational influence, and stability—are preserved.
The principle of energy shadow and intersectional diameter controlling the gravitational force was applied to the visible Universe. Figure 11 shows the model used to calculate the gravitational force between the solar planets and the Sun.
Figure 11: Energy shadow picture. Energy shadow is the cause of a gravitational force [1].
In the situation when objects like stars and planets are separated by a certain distance, the equation for the intersection diameter is:
Dx = 2 (R1*R2) / R (9)
R1 = D/2 and R2 = d/2
Dx = Diameter of the bottom of an energy Shadow cone on a star. dx = Diameter of the bottom of an energy Shadow cone on the planet. Geometrically Dx = dx.
The Gravitational Force model was derived using the Dx factor and applied to the planets of the solar system and the Sun. Also, it was applied to the Earth and Moon [1].
Gravitational force = 2*K* (MCS1+MCS2)*C2 * MCS2*((D/Dx2) + (d/dx2)) (10)
But Dx2 = dx2
Hence, Gravitational force = 2*K (MCS1+MCS2)*C2*MCS2*(D+d)/ Dx2 [1] (11)
When two objects come closer due to the cancellation of the energy lines of the two objects, distortion occurs in the lines of energy.
According to Equation 1,
MCS1 is the mass of the shadow cone of Object 1, which is starved for energy (Unit kg)
MCS2 is the mass of the shadow cone of Object 2, which is starved for energy (Unit kg). MCS1> MCS2.
K is a new gravitational constant 1.5711*10-35 kg-1
C = Velocity of light 3*108 m/s
R = shortest distance between two objects
Hans Hermann Otto [3] further modified the equation for the gravitational force in the new theory by incorporating the Universal gravitational constant G (6.743*10^-11 m3 kg−1 s−2) into equation 1. The modified Gravitational Force equation is Gravitational force=2*7.978975*G*MCS1*MCS2/(Dx/2)^2.
G is the universal gravitational constant: 6.743*10(-11) m3 kg−1 s−2.
The gravitational forces computed by both equations are nearly identical and are summarised below. Additionally, the results are compared with those obtained from the Newtonian equation (Table 7).
| Table 7: Gravitational force computation with the current model and comparison with the Newtonian model. | ||||
| STAR / Sun | Mass Kg | F (Newtons) = 2*7.978975*G*M*m/(Dx/2)^2 | F (newtons) using Newton’s Law | F/F newton |
| SUN | 1.99E+30 | |||
| Murcury | 3.29E+23 | 1.33E+22 | 1.31E+22 | 1.015362916 |
| Venus | 4.87E+24 | 5.53E+22 | 5.54E+22 | 0.998694237 |
| Earth | 5.97E+24 | 3.42E+22 | 3.54E+22 | 0.965311632 |
| Mars | 6.42E+23 | 1.79E+21 | 1.64E+21 | 1.091256371 |
| Jupiter | 1.90E+27 | 4.55E+23 | 4.16E+23 | 1.093520382 |
| STATERN | 5.68E+26 | 3.45E+22 | 3.69E+22 | 0.936749448 |
| URANUS | 8.68E+25 | 1.32E+21 | 1.40E+21 | 0.946816822 |
| NEPTUNE | 1.02E+26 | 6.78E+20 | 6.68E+20 | 1.014711452 |
| PLUTO | 1.31E+22 | 5.37E+16 | 5.55E+16 | 0.967197185 |
| MOON and Earth system | Moon 7.35E+22 | 1.97E+20 | 2.03E+20 | 0.972369844 |
In the visible range, the energy shadow and Dx models yield results that match Newtonian values.
Black holes thus represent the macroscopic limit of the exact geometric interaction mechanism responsible for quark confinement at the quantum scale. In both regimes, force divergence arises from the collapse of the intersection diameter Dx, establishing a continuous and unified description of interaction across all physical scales (Table 8).
| Table 8: Unification summary of gravity over three regions of the Universe. | ||
| GRAVITATIONAL FORCE = 63.8318×G×MCS1×MCS 2/(Dx)^2 |
GRAVITATIONAL FORCE = 63.8318×G×MCS1×MCS2/(Dx)^2 | GRAVITATIONAL FORCE = 63.8318×G×MCS1×MCS2/(Dx)^2 |
| MCS1 IS THE MASS OF A BIGGER QUARK, AND MCS2 IS THE MASS OF A SMALLER QUARK | MCS1 IS A MASS OF A STAR, AND MCS2 IS A MASS OF A PLANET | MCS1 IS THE MASS OF THE BLACK HOLE SHADOW REGION, AND MCS2 IS THE MASS OF THE OBJECT ENTERED IN THE BLACK HOLE |
| MCS1 TAKES THE VALUE OF MCS2 AS ENERGY SHADOW IN THE COMPOSITE STATE, EQUAL TO THE MASS OF THE SMALLER OBJECT |
MCS1 IS THE SHADOW AREA OF THE STAR, AND MCS2 IS THE SHADOW AREA OF THE PLANET | MCS1 AND MCS2 ARE THE SAME IN VOLUME OF MCS2 (WHICH IS SMALLER IN SIZE). MCS1 IS HAVING A HIGHER MASS AS A HIGHER DENSITY OF A BLACK HOLE. MCS1= MCS2 * (DENSITY OF BLACK HOLE / DENSITY OF THE OBJECT) |
| GRAVITATIONAL FORCE = 63.8318×G×MCS2^2 /(Dx)^2 |
GRAVITATIONAL FORCE = 63.8318×G×MCS1×MCS 2/(Dx)^2 |
GRAVITATIONAL FORCE = 63.8318×GX MCS1×MCS2 /(Dx)^2 |
| Dx = Diameter of a cross-sectional circle at the boundary of 2 objects R= Centre to Centre distance between 2 quarks. R1 is the Radius of a smaller quark, and R2 is the radius of a bigger quark. |
Dx= 2 (R1*R2) / R Dx = Diameter of the bottom of an energy Shadow cone on a star. dx = Diameter of the bottom of an energy Shadow cone on the planet D is the diameter of the star, d = diameter of the planet R= Centre to Centre distance between 2 stars and planet |
Dx = Diameter of a cross-sectional circle at the boundary of 2 objects R= Centre to Centre distance between the black hole and the object. R1 is the Radius of the entered object, and R2 is the radius of a Black Hole. |
| R < R1+R2 | R> R1 | R< R1+R2 |
| Energy for the escape of one quark from another reaches an extreme impossible to achieve value as Dx tends to zero when R gets closer to R1+R2 | Applicable when R> R1 | Energy for the escape of an object from a black hole reaches an extreme, impossible to achieve value as Dx tends to reach zero when R gets closer to R1+R2 |
The current theory is based on the following principles:
- The universe is driven by an external energy source
- Force between objects is inversely proportional to the energy shadows of the objects on each other.
- Space-Time quanta are the fundamental building blocks that are instrumental in governing the Universe
Authors have proposed space-time quanta as a fundamental building block theory [2], offering an alternative to the Big Bang model of the Universe's origin. In this theory, external force propagates the Universe. In the current study, it has been confirmed that the external forces can contribute to the formation of new particles, supporting the concept of the Universe evolving in a smoother, rather than an explosive, manner.
This model mathematically confirms the behaviour of quarks and black holes. Because the model applies to particles at the quantum level and to black holes, it supports the theory that external forces govern the universe and that space-time quanta are its fundamental building blocks. As applied energy increases, the energy stored in the quarks increases, resulting in the cleavage of quarks and the formation of new quarks. This principle applies to our theory of the origin and evolution of the universe, in which space-time quanta multiply as the external force acting on them increases.
In this sense, black holes and confined quarks represent two extreme manifestations of a single geometric interaction principle governed by the collapse of the intersection diameter. Dx.
Figure 12 illustrates the Gravitational Force as a function of separation R. In the case of a black hole and a Quark scale, the rise in force is exponential, whereas it is not that sharp on the visible scale.
Figure 12: Graphical representation of the theory.
Gravitational Force Equation for all 3 regions of the Universe:
F α c unified *G*M*I
G is the Gravitational constant
M, Mass factor = (M1*M2); It is the product of the shadow masses of the two objects
I, Inertia Factor = 1/Dx2; Dx is the diameter of the intersection of two objects. In the visible region, there is no intersection; hence, it is the diameter of the bottom of the shadow cones.
Subatomic region: The Inertia factor is dominant as Dx is very small. Mass Factor is the square of M2 (mass of the smaller object). Both objects are in a composite state, and hence the shadow mass of each object is equal to the mass of the smaller object. Hence, the Mass factor is M22. Both objects have almost the same densities.
Black hole region: Rise in the Inertia factor is exponential as the object and the black hole touch each other due to the collapse of Dx. As an object approaches a black hole, it enters a superposition and no longer exists as a separate entity. Hence, Mass Factor is (Volume of Object x Black Hole density) x (Mass of object).
In the visible region, objects do not touch one another. The inertia factor increases with distance, but the mass factor decreases with distance R.
The Unification of the Gravitational force across three regions of the Universe with a single formula is based on the assumption that the Universe receives energy from external sources. Hence, unification provides evidence for the assumption that the Universe is driven by external forces.
This paper presents a complete and compelling alternative view of the universe's fundamental forces, achieving a unified framework from the quantum to the cosmic scale. The Unified Mass-Inertia Force Equation successfully models all regimes: aligning with Newtonian physics at the macroscopic level, geometrically replicating the functional form of the strong force (confinement) at the quantum level, and providing a rigorous physical description of Black Holes. The force law’s dependence on , rather than the traditional Provides a continuous, scale-dependent transition between weak long-range forces and strong short-range repulsion. This removes the need for empirically determined potentials, such as the QCD string tension, and eliminates the curvature singularities of General Relativity. The model offers a geometric origin of inertia and gravitational attraction and predicts new physical phenomena, including attometer-scale deviations from Newtonian gravity and shadow-interference radiation. In addition to providing a unified geometric mechanism for gravitational attraction and quark confinement, the present framework offers a novel perspective on black hole physics. Within this model, black hole capture is not governed by spacetime curvature singularities or event horizons as fundamental entities, but by the geometric collapse of the intersection diameter “Dx”. between energy-shadow regions of the black hole and infalling matter.
In this sense, black holes and confined quarks represent two extremes of a single geometric interaction principle governed by the collapse of the intersection diameter Dx.
- Bhandari PN, Bhandari NM. Int J Phys Res Appl. 2023;6:167–179.
- Bhandari PN, Bhandari NM. Int J Phys Res Appl. 2025;8(12):303–315.
- Reciprocity relation between alternative gravity formulas [Internet]. ResearchGate; [cited 2026 Jan]. Available from: https://www.researchgate.net/publication/380187044
- Otto HH. J Appl Math Phys. 2024 Apr;12(4).
- Wikipedia contributors. Quark [Internet]. Wikipedia, The Free Encyclopedia; 2026 [cited 2026 Jan]. Available from: https://en.wikipedia.org/wiki/Quark
- Emergent physics in the gap between the Planck scale and the size of quarks [Internet]. Physics Stack Exchange; [cited 2026 Jan]. Available from: https://physics.stackexchange.com/q/444196
- Nave CR. Quarks [Internet]. HyperPhysics. Georgia State University; [cited 2026 Jan]. Available from: http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/quarkd.html
- Wigmans R. Getting your quarks in a row. Am Sci. 2003;91(6).