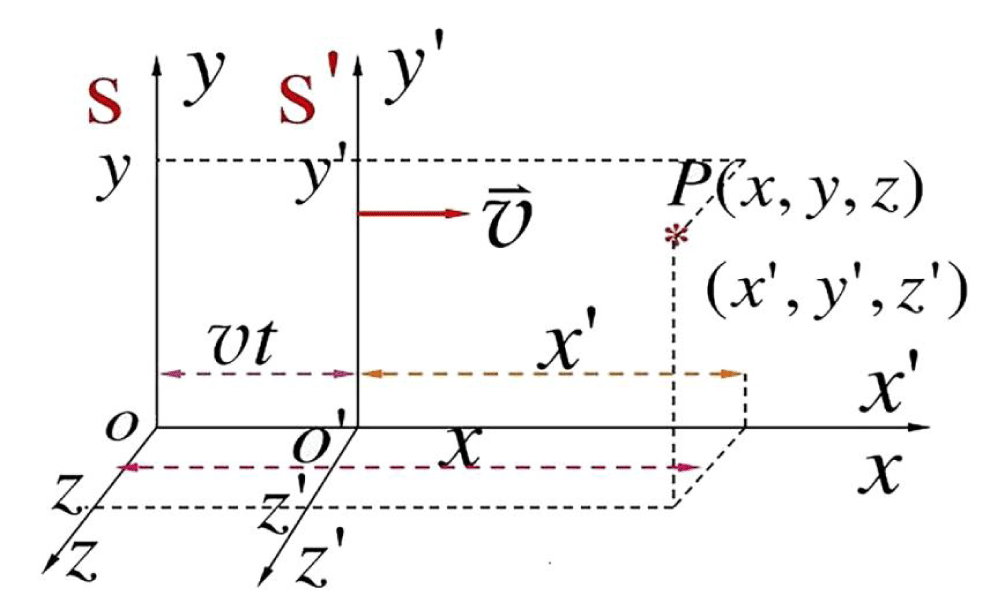This paper presents a new perspective on unified field theory, aiming to unify the four fundamental interactions in nature—gravity, electromagnetism, the weak nuclear force, and the strong nuclear force—by redefining the basic concepts of space, time, and motion. The author proposes that the universe consists solely of objects and the space surrounding them, and that all physical phenomena are descriptions of the motion of objects in space and the motion of space itself. Time is defined as the observer's perception of the movement of surrounding space, and the speed of light is viewed as an embodiment of the unification of space and time. By establishing a mathematical model of spiral motion in space, the paper explains the origin of physical concepts and reinterprets fundamental physical quantities such as mass, charge, and energy. The author also explores how the spiral motion of space leads to the unification of the four fundamental forces and discusses the essence of the invariance of the speed of light. This work aims to provide a new theoretical framework that deepens our understanding of the universe's fundamental laws and opens new avenues for the development of physics.

Unified Field Theory was first proposed by Einstein, who dedicated over forty years to unifying the electromagnetic and gravitational fields but ultimately did not succeed [1]. Currently, four fundamental forces have been identified in nature: the weak force, the electromagnetic force, the gravitational force, and the nuclear force. Among these, the electric and magnetic forces have been successfully unified, while our understanding of the nuclear force remains incomplete [2]. Additionally, the weak and electromagnetic forces can be combined through the electroweak unification theory [3].

This paper posits that electric and magnetic forces are not manifestations of a single force but are instead distinct and independent forces. We will explore the unification of electric force, magnetic force, gravitational force, and nuclear force. In simple terms, this involves expressing these forces within a single mathematical framework and elucidating the relationships among them. Unified field theory encompasses a range of fundamental physics issues, including time, space, motion, force, the speed of light, velocity, mass, charge, energy, and momentum. Consequently, achieving its completion not only holds significant scientific importance but also presents substantial challenges.

The concept of a point particle discussed in this paper serves to simplify the description of an object's particle motion by disregarding the specific shape and size of particles, idealizing the object as a point. In this context, discussing the volume and geometric length of point particles is meaningless, as it contradicts our assumptions. Unified field theory posits that the properties of a point particle originate from its motion in space or the motion of the surrounding space itself; therefore, discussing the internal structure of point particles is irrelevant. Unified field theory primarily describes the motion of space surrounding an object (or point particle) and can thus also be referred to as spatial kinematics. Its fundamental assumption is that the space surrounding an object expands outward at the speed of light. Based on this assumption, we have interpreted, modified, and extended Newtonian mechanics [4], relativity [5] and Maxwell's equations [6], thereby deepening our understanding of these theories.

The core idea of unified field theory is that the physical world is illusory, and all physical phenomena are merely human descriptions. The fundamental principle of unified field theory asserts that all physical concepts originate from the observer's description of motion. In the universe, there are two most fundamental forms of motion: one is the movement of objects within space, and the other is the motion of space itself surrounding the objects. The most basic physical concepts arise from these forms of motion, providing intuitive sensations to the observer. By analyzing, describing, and generalizing these sensations, we develop physical concepts. In everyday life, we constantly perceive the passage of time, which can be viewed as the sensation resulting from objects moving in space or the surrounding space moving, as experienced by the observer. A more plausible perspective is that time is the observer's perception of the movement of space around their body.

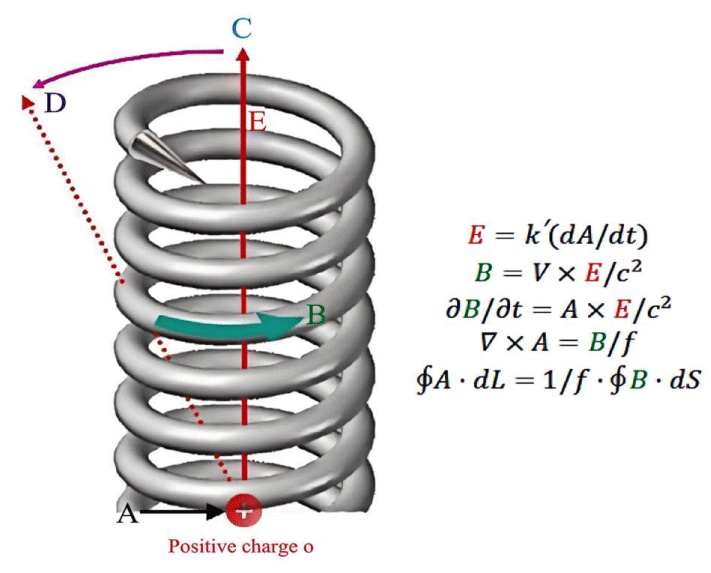
Building upon the fundamental assumption of unified field theory—that all objects in the universe and the space surrounding them expand outward in a cylindrical spiral form at the speed of light—we can provide a physical definition of time: the space surrounding any object in the universe expands outward from the object's center in a cylindrical spiral at a vector speed of light. This spatial motion is perceived by the observer as time. Although some argue that time exists in a universe without humans and that it is merely a human sensation, this viewpoint is incorrect. Time is precisely the physical concept formed by humans' perception of the movement of space around them. Figure 1 illustrates the schematic diagram of the spatial spiral motion model in unified field theory.

Clarification of foundational redefinitions

Unified Field Theory (UFT) rests on three non‑standard but mutually consistent redefinitions. Space is taken as a self‑sustaining entity that continually executes a right‑handed spiral motion; it is neither made of nor convertible into anything more fundamental. Time is not an independent dimension but the observer’s sensation of that spiral motion; whenever the surrounding space displaces, the observer labels the experience as the passage of time. Motion, therefore, has two faces — the travel of objects through space and the autonomous motion of space itself. All familiar physical quantities (mass, charge, field strength, momentum, energy) are interpreted as different descriptive layers that arise when observers track these two kinds of motion from various angles or scales. Putting these elements together defines UFT’s theoretical contribution: it supplies a single kinematic narrative from which classical mechanics, relativity, and known field interactions can be re‑expressed without invoking extra postulates about separate forces or hidden dimensions.

Basic concepts and theoretical framework

The composition of the universe and the basic principles of unified field theory: The universe is composed of objects and the space surrounding them, with no third entity coexisting alongside these. All physical phenomena and concepts are descriptions made by us, the observers, of the motion of objects within space and the motion of space surrounding objects. Without our descriptions, the universe would fundamentally consist only of objects and space; everything else would cease to exist, as it is merely a result of our descriptions of objects and space. The universe we see and perceive is illusory, while the true universe behind it is composed of objects and space.

Space and objects are not composed of something more fundamental, and they cannot be transformed into one another. The universe is dualistic, not monistic. The human brain generates different descriptive modes for objects and space in the universe, giving rise to the geometric world and the physical world. When we describe the motion of objects and the motion of space, the physical world emerges; when we describe the size, quantity, direction, and structure of objects and space, the geometric world is formed. The physical world is primarily processed by humans based on sensory perceptions, whereas the geometric world is developed through rational reasoning.

Both the physical world and the geometric world are products of our descriptions as observers. Without observers, neither the physical world nor the geometric world would exist; only objects and space would exist independently.

The primary distinction between the physical world and the geometric world lies in their focus and complexity. Physics primarily describes motion or phenomena that arise from motion. In contrast, the geometric world represents the initial and straightforward processing of objects and space in the universe by the human brain. While the geometric world involves basic, simple interpretations, physics entails deep and complex analysis of objects and space, particularly concerning the description and manipulation of motion.

Compared to physics, geometry has a broader scope and is closer to the fundamental essence of the universe. Mathematics inherently includes geometry, and in reality, it also encompasses physics. We can thus consider physics as the segment of mathematics dedicated to describing motion.

As for why the universe is composed of objects and space, and why objects and space cannot be transformed into one another, unified field theory does not provide answers to these questions. Instead, unified field theory simply acknowledges this fact and uses it as the foundational premise for further reasoning. The primary objective of unified field theory is to explain the nature of fundamental physical concepts such as time, displacement, mass, charge, gravitational field, electric field, magnetic field, nuclear force field, energy, the speed of light, velocity, momentum, universal gravitation, electromagnetic force, nuclear force, and motion, as well as the relationships among them.

Definition of matter

Matter is anything that exists objectively, independent of observers. In the universe, only objects and space can exist truly and independently; therefore, matter is composed of objects and space. Everything beyond objects and space is a description created by humans, and without the presence of observers, such descriptions cannot exist. For example, the trees and rivers we see before us are "objects," while the growth of trees and the flow of river water are "events." In the universe, objects and space belong to "matter," whereas time, displacement, mass, charge, fields, energy, the speed of light, velocity, momentum, force, temperature, and sound are "events." These properties arise from the motion of matter relative to the observer and are formed through the observer's descriptions.

This fundamental principle rejects the notion that energy and time are part of matter, and it also denies that fields are a special kind of matter. Instead, fields can be viewed as effects caused by the motion of material particles or the movement of space. Unified field theory posits that the essence of a field lies in the effects triggered by the dynamic and changing space.

The space of the universe is infinite, and the objects within it are also boundless. Time is merely a human perception and description of spatial motion, defined as a physical quantity by the observer. As long as observers exist, time in the universe likewise exists. The universe has no beginning or end; its space and age are both infinite. Therefore, the Big Bang theory can only account for local phenomena within the universe, and the notion that the entire universe originated from the Big Bang is incorrect.

The origin of physical concepts

Physics represents the observer's perception of the motion of objects and space, shaped through descriptions generated by the brain. The physical world we see and feel is, in reality, illusory and ceases to exist without observers. What truly exists is the geometric world composed of objects and space. The geometric world is closer to the fundamental essence of the universe, whereas the physical world is the observer's brain's description and processing of the geometric world. Therefore, discussing how objects and space are generated or their origins is meaningless, as objects and space are the most basic elements constituting the universe and cannot be formed from something more fundamental.

Objects can transform from one form to another, but do not spontaneously appear or disappear. Both objects and space inherently exist, much like the existence of the universe itself; therefore, discussing how the universe originated or its inception is equally meaningless. We cannot define objects and space in terms of something more fundamental, as there is nothing more basic than them. However, we can use objects and space to define other physical concepts. All physical phenomena and concepts fundamentally arise from the sensations produced by the motion of objects and space, and physical concepts are the result of the brain processing and interpreting these sensations.

Beyond objects and space, all other physical concepts—such as time, fields, mass, charge, the speed of light, force, momentum, and energy—are properties exhibited by objects in motion within space or by the space surrounding objects themselves relative to an observer. These properties are formed through motion and are therefore related to displacement. It can be considered that time, fields, mass, charge, the speed of light, force, momentum, and energy are all functions of spatial displacement, and we can represent them using spatial displacement.

In physical concepts, phenomena like sound, color, force, and temperature are sensations triggered in observers when objects move through space. We analyze and generalize these sensations to form the corresponding concepts. However, fields and time possess their special characteristics: a field is an effect resulting from the motion of space surrounding an object, while time is the observer’s perception of the movement of space around themselves.

Basic physical concepts and their classification

Within the realm of physical concepts, some are fundamental, while others are derived from these foundational ideas. For instance, time and displacement are considered fundamental concepts, whereas velocity is derived from the combination of time and displacement. Since the universe is composed of two primary elements—objects and space—these two constitute the most basic physical concepts. They form the very foundation of the universe and cannot be further defined in terms of more fundamental entities. All other physical concepts can be defined and understood through the interactions and relationships between objects and space.

Below is a schematic diagram illustrating these physical concepts from higher to lower levels: Objects (or Point Particles), Space → Time, Displacement, Fields → Velocity, Speed of Light → Mass, Charge → Momentum → Force → Energy, Work → Temperature, Light, Sound, Color, etc.

This hierarchy demonstrates how more complex physical concepts are built upon more fundamental ones. For example, objects and space are the most basic elements, serving as the foundation for all other concepts. Time, displacement, and fields arise from the interactions and movements of objects within space, while velocity and the speed of light are derived from the fundamental concepts of time and displacement. Mass and charge emerge from the properties of objects as they move through space, and momentum is a consequence of mass in motion. Force results from interactions involving momentum, and energy and work are derived from the application of force. Furthermore, temperature, light, sound, and color are derived from energy interactions and the movement of objects, affecting the observer's perception. This classification underscores the interconnectedness of physical concepts, illustrating how complex phenomena are systematically built from more elementary principles.

Basic physical quantities are divided into two main categories: scalars and vectors. Scalars are quantities that can be expressed solely by numerical values, whereas vectors encompass both magnitude and direction. Scalars can be further classified into positive and negative scalars, as well as pure scalars that do not possess a positive or negative distinction. For example, a positive charge is a positive scalar, and a negative charge is a negative scalar.

General definitions of the four fundamental fields in the universe

In mathematics, a field is defined as a space in which every point is associated with a specific quantity. If the quantity at each point in space is a scalar, the space is referred to as a scalar field. Conversely, if the quantity at each point is a vector, the space is termed a vector field [7]. According to this definition, a field can be represented by a function defined at every point in space; conversely, if a function is provided for each point within a given space, a field can also be defined.

In physics, we associate the gravitational field, electric field, magnetic field, and nuclear force field with the motion of space, considering the four fundamental fields in physics—the gravitational field, electric field, magnetic field, and nuclear force field—to collectively constitute a space characterized by cylindrical spiral motion. In unified field theory, the weak force field is not considered a fundamental field; instead, it is a combination of the electric field, magnetic field, and nuclear force field.

The electric field and magnetic field are not the same because their directions sometimes do not align, preventing them from being superimposed or directly interacting. However, fields of the same type can be superimposed, subtracted, and interact with each other. Therefore, we can provide a unified definition for the four fundamental physical fields and subsequently offer precise definitions for each field.

This approach allows for a coherent framework in which the fundamental interactions are interconnected through the motion of space, emphasizing the unique characteristics and interactions of each field within the unified field theory.

The unification of the four physical fields is defined as: relative to the observer, any spatial point p in the space Ψ around the particle o, the displacement vector from o point to p point (bit vector) , changes with the spatial position (x, y, z) or with time t, such space Ψ is called physical field can also be called physical force field. This definition encapsulates how each of the four fundamental fields—gravitational field, electric field, magnetic field, and nuclear force field—is are manifestation of the displacement vectors within the space surrounding a point particle. The variation of these vectors concerning spatial coordinates and time underscores the dynamic nature of these fields, linking them intrinsically to the motion of space itself. By establishing this unified definition, we can systematically describe each fundamental field in terms of the underlying spatial displacement vectors, facilitating a coherent framework for understanding their interactions and interrelationships within the unified field theory.

From a mathematical perspective, a field is the derivative of the displacement vector of the space surrounding an object concerning spatial position or time, effectively representing the degree of motion of space relative to the observer.

In practical applications, we define the four fundamental physical fields by measuring the degree of motion in the space surrounding an object. This approach aligns with the basic principles of unified field theory, which assert that all physical phenomena arise from the motion of a point particle or the space surrounding a point particle relative to the observer. In simple terms, a field is the moving space, and the effects of the field are the results of this spatial motion. The influence of a field on an object occurs by altering the object's position in space or by inducing a tendency for its spatial position to change, thereby acting upon the object.

From this, it can be seen that the four fundamental physical fields are all vector fields. The different fields are simply different manifestations of the cylindrical spiral motion of space, observed from various angles and perspectives by the observer. It is important to emphasize that a field describes the motion of the space surrounding a point particle relative to the observer. The four fundamental conditions—space, point particle, observer, and motion—are all essential and cannot be omitted (in certain special cases, the point particle and the observer may be the same).

Additionally, fields manifest in three primary forms: their distribution within three-dimensional space, across two-dimensional curved surfaces, and along one-dimensional curves. To describe these various manifestations, we can employ several mathematical theorems. Gauss's Theorem allows us to characterize the distribution of a field in three-dimensional space and on curved surfaces through the concept of divergence [8,9]. Stokes' Theorem facilitates the description of a field's distribution on curved surfaces and along curves using the concept of curl [10]. The Gradient Theorem aids in describing the distribution of physical quantities in scalar fields along curves [11,12]. Fundamentally, a field is a space characterized by cylindrical spiral motion, which is a combination of rotational motion and linear motion perpendicular to the plane of rotation. Divergence describes the linear motion component within the space, while curl accounts for the rotational motion component. This comprehensive framework underscores how mathematical principles can effectively describe the complex behaviors and distributions of physical fields in various spatial dimensions.

The nature of space, time and motion

How to describe the motion of space itself: Unified Field Theory posits that space itself is in constant motion. While modern physics primarily describes the motion of objects within space, how can we qualitatively and quantitatively describe the motion of space itself? To address this, we can divide space into many small units, each referred to as a "spatial geometric point" or "spatial point." The trajectory of these spatial points' movement is termed a "spatial line." By describing the movement of these spatial points, we can characterize the motion of space itself. Mathematical methods used in fluid dynamics and wave equations can also be applied to describe the motion of space. We treat space as a special medium analogous to a fluid. This analogy allows us to apply analytical tools from fluid dynamics to better understand and express the dynamic behavior of space.

Why do objects and space have to move in the universe

Physics is our description of the geometric world, which is composed of objects and space. Therefore, every physical phenomenon can be associated with a corresponding geometric state. In physics, the states of motion we describe are equivalent to the states of orthogonality in geometry. In the absence of an observer's descriptions, a state of motion is essentially a state of orthogonality in geometry. It is important to note that this section involves a reasoning process, as each state of motion must correspond to a specific geometric state, the exact form of which requires certain assumptions.

Unified Field Theory explains why objects and space must move through the "Vertical Principle." The Vertical Principle is articulated as follows: relative to an observer, any object in the universe can form up to three mutually perpendicular straight lines at every point in the surrounding space. This configuration is referred to as the three-dimensional orthogonal state of space. Any spatial point in this orthogonal state is compelled to undergo motion, and its direction and trajectory of movement will continuously change, thereby allowing the formation of new orthogonal states.

This principle underscores the inherent dynamism of space and objects within the universe. By establishing that spatial points must move and continuously reorient themselves, the Vertical Principle provides a foundational explanation for the perpetual motion observed in both objects and the space that envelops them. This dynamic interplay between objects and space is fundamental to understanding the behavior of the universe as described by Unified Field Theory.

The above provides a qualitative description of the Vertical Principle. Next, we will further offer a quantitative description of the Vertical Principle. Because the direction of motion continuously changes, the motion must inherently be along a curved path. In circular motion, a maximum of two mutually perpendicular tangent lines can be formed. However, since space is three-dimensional, at any point along the trajectory of motion, three mutually perpendicular tangent lines can be established. Therefore, linear motion is superimposed in the direction perpendicular to the plane of circular motion.

Therefore, it is reasonable to posit that spatial points move in a cylindrical spiral manner—a combination of rotational motion and linear motion perpendicular to the plane of rotation. Objects exist within space, and the motion of space itself causes the positions of these objects to change. This explains why all objects in the universe are in motion. Typically, we attribute the motion of objects to the presence of forces, but such an understanding is superficial. In reality, the motion of all objects in the universe is driven by the motion of space itself. Consequently, we can also interpret the nature of force in terms of the motion of space.

Objects can influence the space surrounding them, thereby affecting other objects within that space. This means that objects interact through space without the need for any special medium to transmit interaction forces. Objects exist within space and can exert influence on the surrounding space, with the extent of this influence measurable by the degree of space's motion. When an object affects the surrounding space, causing it to move, the movement of space inevitably impacts the positions of other objects within it, leading them to move or exhibit tendencies toward changes in their motion.

Interactions between objects, such as gravitational force, electric force, magnetic force, and nuclear force, are realized through the motion of space itself. Objects transmit forces by altering the state of motion of space. Space exists objectively, independent of observers, and can indeed be regarded as a special medium. Regarding whether it is the objects that cause space to move or the motion of space that causes objects to move, we should understand this as a mutually causal relationship, where neither can be considered primary over the other. Objects and space are closely interconnected.

It is also important to note that the description of space's motion has similarities and differences compared to the description of ordinary object motion. Unified Field Theory describes space motion as the motion of space surrounding objects. Without objects, simply describing the motion of space is meaningless, because describing motion requires determining the initial moment and the initial spatial positions. Space alone cannot establish these initial conditions. The motion of space itself begins with objects and ends with objects; without objects or observers, it is meaningless to describe the motion of space alone.

The Vertical Principle is one of the universe's core secrets and is intimately related to spiral motion. In physics, Faraday's principle of electromagnetic induction is also connected to the Vertical Principle. Additionally, mathematical concepts such as the vector cross product and curl are deeply intertwined with the Vertical Principle.

The spiral motion law

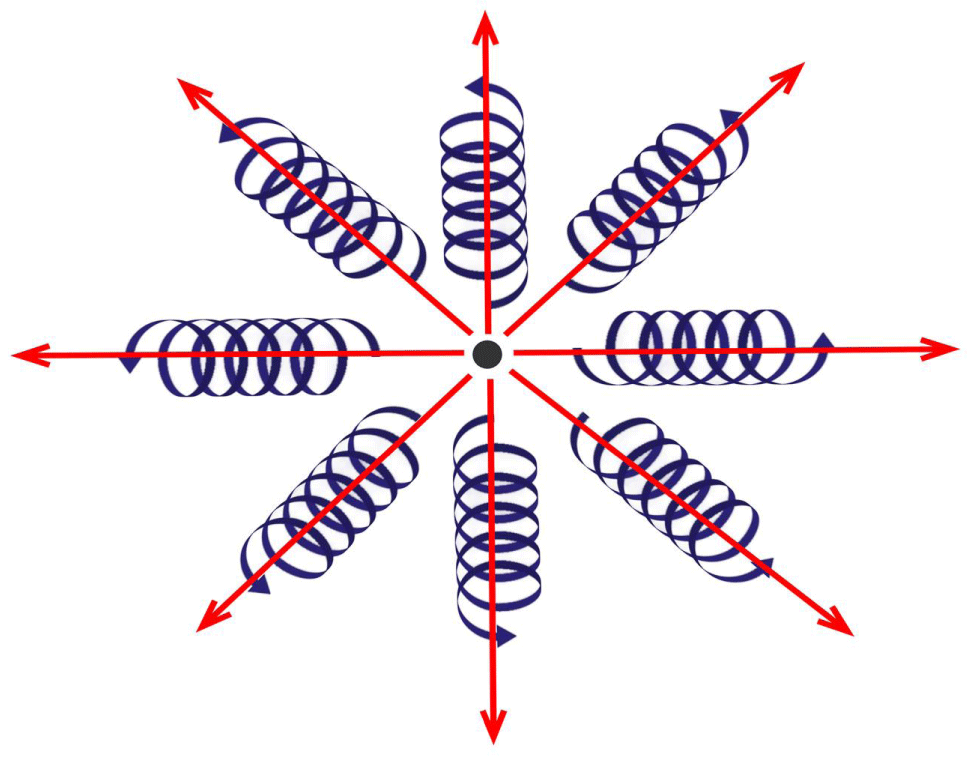
Everything in the universe, from electrons, photons, and protons to Earth, the Moon, the Sun, and the Milky Way, all freely existing point particles in space, move in a spiral manner without exception, including space itself, which also moves in a cylindrical spiral manner. The spiral motion law is one of the core laws of the universe. Everything in the universe appears to be in perpetual motion, but it is not closed.

Continuity and discontinuity of space

Human cognition and the processing of space typically assume that space is continuous. Most mathematical systems also default to space being continuous. However, in certain special circumstances, space may exhibit discontinuity. For example, when an object moves at the speed of light relative to an observer, the spatial length in the direction of motion contracts to zero. In this situation, the space surrounding the object can appear discontinuous relative to the observer. This phenomenon is closely related to quantum entanglement in quantum mechanics and is one of the fundamental reasons for the occurrence of quantum entanglement.

Description of motion cannot be separated from the observer

Relativity posits that physical concepts such as time, displacement, electric field, magnetic field, force, mass, etc., are relative. Different observers may measure different values; this “relativity” is relative to the observer. In reality, these physical concepts—time, displacement, velocity, force, mass, energy, etc.—all originate from the motion of objects relative to us, the observers, or from the motion of space itself surrounding the objects. Therefore, describing motion without the observer or without specifying a particular observer is meaningless. Physical quantities like time, displacement, velocity, force, mass, energy, etc., lose their actual meaning.

The correct understanding should be that all motion in the universe must be defined relative to an observer. Without observers, the universe’s scene would be like a frozen photograph, not “non-existent.” The state of motion in physics, from a geometric perspective, is essentially the “orthogonal state.” These two phenomena are based on the same principle, only observed from different angles (physical perspective and geometric perspective), resulting in different appearances. The state of motion is essentially the observer’s continuous process of affirming and negating the position of objects in space. It is important to note that when describing motion in physics, space, objects (or point particles), and observers are all indispensable; otherwise, motion itself loses its meaning. Regarding the description of time changes, in reality, the observer and the object are the same entity—our human bodies.

Human understanding of motion has undergone a developmental process. Newtonian mechanics posits that to describe an object's motion, one must select a reference object considered to be at rest as a baseline, with the description of motion focusing on the path traversed by the object over some time. Newtonian mechanics asserts that the measurement of time and space is independent of the observer's motion.

Relativity inherits the basic framework of Newtonian mechanics but emphasizes that different observers may measure different values for physical quantities such as space and time, especially when relative velocities approach the speed of light. Relativity contends that the measurement of time and spatial length depends on the observer's state of motion.

Unified Field Theory, on the other hand, maintains that the description of motion must be relative to a specific observer. Without an observer or without specifying a particular observer, describing motion becomes meaningless. In physics, states of motion and even states of rest are results of the observer's descriptions. Without an observer, there is no definition of motion or rest; the universe would consist only of objects and space. Without a specified observer, it is impossible to determine whether objects and space are in motion or at rest, making discussions of motion or rest meaningless in such contexts.

Choosing a reference frame to describe motion is sometimes unreliable. Unified Field Theory posits that time is formed by the observer's motion within space and is certainly related to the observer's state of motion. In other words, the measurement of time is dependent on the observer, and different observers in relative motion may derive different results for the duration of the same event. Since space itself is continuously in motion, the displacement of space is also related to the observer's motion, leading to different measurement outcomes for different observers.

Like Relativity, Unified Field Theory emphasizes that the measurement of time and space varies depending on the observer in relative motion and that these variations should not be confused.

Why space is three-dimensional

We know that at any point in space, up to three mutually perpendicular directed straight lines can be drawn, which is a fundamental property of three-dimensional space. But why exactly three lines, and not two or four? The reason for this phenomenon lies in the way space moves. If space were only to undergo linear motion, it would form a one-dimensional space; if it were to move along a curved path, it would form a two-dimensional space. In reality, space is undergoing cylindrical spiral motion, thereby resulting in three-dimensional space.

The three-dimensional nature of space originates from space performing a cylindrical spiral motion continuously. Since the three directions in space are equal and no direction is special, all three directions undergo motion simultaneously when space moves. Coupled with the continuity of motion, this restricts space to moving only in a cylindrical spiral manner. In other words, the three-dimensionality of space is formed by cylindrical spiral motion, and these two concepts are mutually causal.

The space we live in is right-handed spiral space, meaning that the thumb of the right hand points in the direction of linear motion of space, and the four fingers wrap around in the direction of space’s rotation, which defines the rotation direction of space.

As for whether left-handed spiral space exists in the universe, logically speaking, if left-handed spiral space does exist, it would be repelled by the universally existing right-handed spiral space. Over billions of years of evolution, left-handed spiral space would be pushed to the infinite outskirts of the universe. Even if such space exists, we would not be able to directly detect it.

Furthermore, when two right-handed spiral spaces encounter each other (from the observer's perspective, their rotation directions are counterclockwise), the rotational contact areas cause space to contract, thereby exhibiting mutual attraction. In contrast, when left-handed spiral space meets right-handed spiral space, they repel each other.

Space can store information infinitely

The definition of information is: information is the form of motion of matter (composed of objects and space). The amount of information can be represented by possibilities; the more possibilities, the greater the amount of information. We categorize the objects of our recognition into "events" and "objects," with information belonging to "events." The amount of information stored or carried by any particle in the universe is always limited.

Any location in the universe can store all the information of the entire universe's past, present, and future. In other words, any piece of space can store information infinitely. The underlying reason is that space is infinitely continuous and can be divided infinitely. This can also be logically deduced: the space surrounding an object moves outward at the speed of light, capable of carrying all the object's information into the surrounding space. Due to the three-dimensional space moving at the speed of light, the spatial length in the direction of motion contracts to zero, transforming into two-dimensional space. Therefore, space moving at the speed of light can instantaneously transmit all of an object's information to any point in the universe, rather than propagating step by step at the speed of light as commonly believed.

There are only two-dimensional and three-dimensional spaces in the universe; one-dimensional or four-dimensional and higher-dimensional spaces do not exist. Due to the zero-volume nature of two-dimensional space, it can maintain zero distance with any three-dimensional space in the universe. Consequently, information in a two-dimensional curved surface space can permeate the entire three-dimensional space of the universe. Conversely, it can also be said that any location in the universe's three-dimensional space inherently contains all the information of the universe's past, present, and future.

Why does it also include future information? Because time is the observer's perception. Without observers, time does not exist. In the absence of observers, all information about the universe's past and future can overlap at a single point in space. Besides the infiniteness of time and space, the universe also possesses the infiniteness of information. The universe encompasses infinite possibilities, and its continuous evolution constantly manifests these possibilities infinitely and repeatedly.

The Relationship between Information Storage and Space: Information occurring in three-dimensional space can be preserved in two-dimensional curved surface space, which can be strictly proven using Gauss's Theorem in field theory. Similarly, information in a two-dimensional curved surface space can be preserved in one-dimensional linear space, which can be proven using Stokes' Theorem in field theory.

It is particularly important to note that the generation of information depends on the participation of material particles. Excluding material particles, space alone cannot create information but can only transmit and store information. Information requires the description of an observer; without an observer, information does not exist.

Basic assumptions and mathematical models of unified field theory

Basic assumptions of unified field theory: In the universe, when any object (including the body of the observer) is at rest relative to the observer, the surrounding space exhibits a cylindrical spiral motion centered on the object, as shown in Figure 2. This motion is the result of the combination of uniform rotational motion and uniform linear motion in the direction perpendicular to the plane of rotation, and it disperses outward at the speed of light (in Unified Field Theory, the speed of light is considered a vector, denoted as , where c remains constant, but its direction can vary).

The motion of space surrounding objects dispersing outward in a cylindrical spiral manner indicates the incorrectness of the Big Bang theory. According to this theory, the universe has no beginning or end and has always existed. It is merely how space and objects move that has led to our misunderstanding of the universe's expansion.

One of the core pieces of evidence for the modern Big Bang theory is the expansion of space relative to any observer. However, the true reason for the expansion of space is that the space surrounding every object in the universe (including the observer) disperses outward in a cylindrical spiral manner at the speed of light, centered on the object. In this motion, the celestial bodies within space are also moving relative to us, the observers. Therefore, the recession of stars is not because the universe exploded from a specific point, but because the space in which they reside is continuously dispersing outward at the speed of light.

A key factor is the initial state of motion of objects and celestial bodies. For example, the Earth was initially in an approximately stationary state relative to us, the observers, and the Moon was in a nearly stationary state relative to the Earth (i.e., at very small relative velocities). In contrast, those stars that are extremely far from us are moving away at relatively higher speeds due to their great distances, making their recession speeds more apparent.

The physical definition of time

Unified Field Theory's fundamental principles indicate that all physical concepts originate from our observers' descriptions of motion. In the universe, there are two most fundamental forms of motion: one is the motion of objects within space, and the other is the motion of space itself surrounding objects. The most basic physical concepts arise from the perceptions we observers receive from the motion of objects in space or the motion of space surrounding objects. By analyzing, describing, and summarizing these perceptions, we form physical concepts.

In our daily lives, we constantly perceive the passage of time, and the essence of time can be understood as the motion of objects within space or the motion of space surrounding objects, providing us with a perception. So, what exactly is moving that gives us the sensation of time passing? Suppose we send a person on a spaceship, flying to a location hundreds of billions of light-years away, then dropping them off and having the spaceship quickly return. In this remote region of space, other planets are extremely far away, having almost no influence. It can be imagined that even though the person is present there, they would still have the sensation of time passing. So, what is moving that makes this person perceive the passage of time?

In this case, the only moving objects are the person's body and the space surrounding them, and they see their own body as stationary; the only source of motion is the space around them. Therefore, the correct understanding should be: time is the perception of the motion of space around our bodies by us, the observers.

Combining the fundamental assumption of Unified Field Theory—that all objects in the universe and the space surrounding them are dispersing outward in a cylindrical spiral motion at the speed of light—we can provide a physical definition of time: the space surrounding any object in the universe (including our observers' bodies) disperses outward from the object at vector speed of light along a cylindrical spiral trajectory. This spatial motion is perceived by us observers as time. In other words, “time” is a physical concept born from human perception of the motion of space surrounding our bodies.

Spacetime unification equation

The above physical definition of time also defines the speed of light. In Unified Field Theory, time, space, and the speed of light are closely related and intrinsically linked. The speed of light reflects the unity of spacetime, meaning that the essence of time is our description of space moving at the speed of light.

We extend the speed of light into a vector form, defined as the vector speed of light $\overrightarrow{c}$ , with a magnitude of c, and a direction that can change with time t、, the velocity of the light source, and the velocity of the observer. It can be expressed as: $\overrightarrow{c}=c\times \widehat{N}$ . Here, c is the scalar speed of light, which does not change with time t、, the velocity of the observer, or the velocity of the light source, while the unit vector $\widehat{N}$ represents the direction of the speed of light. Based on the above physical definition of time, we can consider that time is proportional to the distance traveled by spatial points moving at the speed of light around the observer. Using the concept of spatial points, we can understand time as the sensation generated by numerous spatial points spiraling outward from the observer in a cylindrical spiral pattern at the vector speed of light. Let a certain spatial point p start from the observer's position at time t = 0, and move at the vector speed of light $\overrightarrow{c}$ . The time t experienced is proportional to the distance r it travels. From this, the spacetime unification equation can be derived as follows: $\overrightarrow{r}\left(t\right)=\overrightarrow{c} t=x \overrightarrow{i}+y \overrightarrow{j}+z \overrightarrow{k}$ ( $\overrightarrow{k}$ , are unit vectors along the x-axis, y-axis, z-axis, respectively). In scalar form, the equation can be expressed as: $r^2=c^2 t^2=x^2+y^2+z^2.$ . These equations embody the unification of space and time, similar to the spacetime relativity equations in relativity, reflecting that space and time originate from the same motion. In other words, time can be represented through the spatial displacement of motion at the speed of light.

It is particularly important to note that not only time, but also fundamental physical concepts such as mass, charge, fields, momentum, force, and energy, are caused by and composed of spatial displacement. If we trace the essence of these physical concepts, we find that ultimately they can all be reduced and decomposed into spatial displacement. This also reveals the core nature of physics: physics is fundamentally a discipline that describes motion, and all motion can ultimately be traced back to variations in spatial displacement.

Spiral spacetime wave equation

All objects (or point particles) in the universe, including space itself, move in a cylindrical spiral manner. Spiral motion is one of the most fundamental laws of the universe. Unified Field Theory posits that the space surrounding an object also follows a cylindrical spiral motion. Next, we will establish the three-dimensional cylindrical spiral spacetime equation in Unified Field Theory, serving as an alternative to the four-dimensional spacetime equations in relativity.

Let us consider a spatial region where a stationary point particle exists relative to the observer. Using point O as the origin, we establish a three-dimensional Cartesian coordinate system with axes x, y, and z.

At time t' 0, we consider an arbitrary spatial point p around the object o, whose position is represented by x0,y0,z0. The spatial displacement vector from point O to point P is denoted as. As time t progresses, point p continues to move and reaches a new position x, y, z, at time t, with the corresponding displacement vector denoted as $\overrightarrow{r}$ .

In cylindrical spiral motion, the motion can be decomposed into a vector composition of rotational motion and linear motion. Note that the position vector (displacement vector) and the linear motion vector should not be confused. The position vector can be viewed as the resultant of the rotational vector and the linear motion vector. According to the principles of cylindrical spiral motion, since the spatial positions x, y, z, and time t are dynamically interrelated, we can derive the spacetime relationship as: $\overrightarrow{r}\left(\text{t}\right)=\text{f}(\text{x},\text{y},\text{z}),$ The spacetime unification equation based on the above relationships is: $\overrightarrow{r}\left(t\right)={\overrightarrow{r}}_0+\overrightarrow{c} t=\left(x_0+x\right) \overrightarrow{i}+\left(y_0+y\right) \overrightarrow{j}+(z_0+z) \overrightarrow{k}.$ . This equation can sometimes be simplified as: $\overrightarrow{r}\left(t\right)=\overrightarrow{c} t=x \overrightarrow{i}+y \overrightarrow{j}+z \overrightarrow{k}.$ In scalar form, the equation is expressed as: $r^2=c^2 t^2=x^2+y^2+z^2.$ R is the magnitude of the vector $\overrightarrow{r}$ .

In Unified Field Theory, time, space, and the speed of light are tightly interlinked. Space's motion is described through the speed of light, and the quantity of time is essentially equivalent to the spatial displacement resulting from motion at the speed of light. Unlike the perspective of relativity, which treats time as an equal dimension alongside space and incorporates it into four-dimensional spacetime, Unified Field Theory posits that time is not an independent dimension. Instead, time is the observer's description of spatial motion. The existence of time is virtual and only holds meaning in the presence of an observer.

If point p rotates in the x-y plane with an angular velocity ω, moves linearly along the z-axis with a constant velocity h, and has a projection length R, the motion can be described as: $x=x_0+R cos\omega t,y=y_0+R sin\omega t,z=z_0+h t.$ The above equations can also be expressed using the following vector form: $\overrightarrow{r}={\overrightarrow{r}}_0+\overrightarrow{c} t=\left( x_0+R \cos \omega t\right) \overrightarrow{i}+\left(y_0+R \sin \omega t\right) \overrightarrow{j} +.$ This is referred to as the three-dimensional spiral spacetime equation. Sometimes, this equation can be simplified to: $\overrightarrow{r}=R cos\omega t \overrightarrow{i}+R sin\omega t \overrightarrow{j}+h t \overrightarrow{k}.$

Unified Field Theory posits that all phenomena in the universe—from galaxies to electrons, protons, and even human thoughts—can be described by this equation. The mass, charge, and all physical phenomena of objects are determined by spatial displacement and spiral motion.

In the three-dimensional spiral spacetime equation, rotational motion and linear motion are closely related. The rotational displacement vectors. $\overrightarrow{X},\overrightarrow{Y}$ The rotational displacement vectors $\overrightarrow{X},\overrightarrow{Y}$ along the x- and y-axes, and the spatial linear displacement vector $\overrightarrow{z}$ along the z-axis, satisfy the following cross-product relationships: $\overrightarrow{X}\times \overrightarrow{Y}=\overrightarrow{Z},\overrightarrow{Y}\times \overrightarrow{X}=-\overrightarrow{Z}.$ Here, $\overrightarrow{X}$ and $\overrightarrow{Y}$ represent rotational quantities. If $\overrightarrow{X}\times \overrightarrow{Y}=\overrightarrow{Z}$ denotes a right-handed spiral relationship, then $\overrightarrow{Y}\times \overrightarrow{X}=-\overrightarrow{Z}$ corresponds to a left-handed spiral relationship. These two equations illustrate the connection between rotational motion and linear motion.

For the three-dimensional spiral spacetime equation, the following points should be noted:

Spatial points and position vectors: Around point o, there exist numerous spatial points, with point p being just one of them. In the equation, there is not just a single position vector around a point but a radiating, uniformly distributed array of vectors. Due to the synchronized motion of these vectors, no two spiral lines in space will intersect.

Continuity of spiral motion: Spiral lines originate from the point particle and ultimately terminate at the point particle. In regions of space without point particles, spiral lines do not spontaneously arise. The spiral motion of space is uniform and continuous, without arbitrary interruptions.

Arbitrary choice of coordinate axes: The establishment and choice of coordinate axes are arbitrary and serve merely as mathematical tools to describe space. Therefore, they do not affect the distribution of spiral lines or the motion of space.

Effects of the field: The cylindrical spiral motion of space is essentially a superposition of linear and rotational motions. In field theory, divergence describes the linear component of space, while curl describes the rotational component.

Boundary cases of spiral motion: If x and y are zero, the spatial point moves linearly along the z-axis. The spiral equation still applies and does not need to be converted into a linear equation. In practice, the spiral motion equation remains applicable in extreme cases, such as when x or y approaches zero (where the spiral radius approaches zero), or when x or y approaches infinity (where z approaches zero).

Time derivative and speed of light: By taking the time derivative of the spiral equation, we obtain the vector speed of light. Here, the speed of light is not derived solely from the linear component but from the derivative of the position vector, which includes both rotational and linear displacement components.

Correspondence between spatial points and spiral lines: Each spatial point corresponds to a spiral line, with its radius ranging from zero to infinity, which cannot be specifically quantified in meters. Similar to the distribution of electric field lines around a charge, specific numerical values are not critical.

Breakdown of uniformity: When the point particle is stationary relative to the observer, the spiral motion of space is uniform, and the distribution of spiral lines is continuous. When the point particle begins to move, the uniformity of the spiral lines may be disrupted, particularly when the object's velocity approaches the speed of light, at which point spiral lines may appear to break. Through the above equations and analysis, we reveal how Unified Field Theory uses cylindrical spiral motion to unify spacetime and physical phenomena, as well as how it explains the fundamental principles underlying various physical phenomena in the universe.

Understanding the nature of the speed of light

As physics continues to develop, the concept of the speed of light has become increasingly significant, particularly in its relationship with fundamental physical concepts such as time, space, fields, mass, charge, momentum, force, and energy. In Unified Field Theory, the speed of light is extended to a vector quantity, which not only broadens our understanding of light speed but also deepens our insight into the essence of spacetime.

Unified Field Theory posits that the speed of light reflects the unification of space and time, asserting that space is fundamental and time is formed by the motion of space. Time is essentially the perception and description by us, the observers, of space moving at the speed of light. Therefore, time, space, and the speed of light are intricately interconnected in Unified Field Theory, forming an integrated whole.

Within the framework of Unified Field Theory, the physical definition of time tightly binds space, time, and the speed of light. By defining time through the motion of space, the speed of light is simultaneously defined. Time and space share the same essence, with the speed of light acting as a constant that connects them within spacetime: when space extends, time also extends; when space contracts, time correspondingly contracts. This phenomenon reflects the unification of spacetime, known as the spacetime unification equation. For instance, in an atom, electrons move rapidly within an extremely small spatial range, resulting in very short periods. In contrast, in the solar system, planets move over vast spatial ranges at slower speeds, leading to much longer periods. These phenomena exemplify the effect of spacetime unification at different scales.

Although the spacetime unification in Unified Field Theory and the spacetime relativity in relativity theory appear contradictory on the surface, they are fundamentally consistent. The spacetime unification equation serves as a foundational equation from which the spacetime relativity equations of relativity can be derived.

Relativistic effects associated with the speed of light

Why the speed of light is the maximum speed in the universe: In relativity, the speed of light is considered the maximum speed in the universe. This conclusion is primarily based on mathematical derivations, as certain physical quantities, such as mass and kinetic energy, become imaginary when an object's velocity exceeds the speed of light, losing physical significance. However, logically reasoning why the speed of light is the universal limit is also straightforward.

Imagine a spaceship stationary relative to us with a length of 10 meters. When the spaceship moves at some velocity relative to us, its length contracts, hypothetically reducing to 5 meters. As the spaceship's velocity approaches the speed of light, its length contracts further, eventually reaching zero. If the spaceship's velocity were to exceed the speed of light, would its length become less than zero? Such a scenario is impossible.

Relativity also posits that if a clock is placed inside the spaceship, it will tick more slowly relative to our clock as the spaceship moves. When the spaceship's velocity reaches the speed of light, its length contracts to zero, and the clock inside the spaceship nearly stops, ticking extremely slowly or even freezing entirely.

Now, consider an alien planet 50 light-years away. If aliens from that planet travel to Earth in a spaceship moving at the speed of light, we, as observers, would perceive the spaceship taking 50 years to reach Earth. However, the aliens aboard the spaceship would perceive their journey as taking "zero time," arriving on Earth instantaneously. If faster-than-light travel were possible, this reasoning would imply that an object could traverse infinite distances in less than no time. Such a notion defies logic and is not realistic.

This demonstrates that faster-than-light motion leads to physical and logical contradictions, reinforcing the conclusion that the speed of light is the ultimate speed limit in the universe.

Length contraction and time dilation: observer effect or real effect?

The discussion above involves two famous effects in relativity—length contraction and time dilation. When an object's length becomes zero, its volume also reduces to zero. By conventional reasoning, an object with zero volume would cease to exist. However, relativity concludes otherwise, which many find difficult to accept. Some argue that this is merely an observer effect, meaning that it is a phenomenon caused by the observer's measurement rather than an actual change in the object itself.

On the other hand, some believe that length contraction and time dilation are not merely observer effects but real effects caused by relative motion. Unified Field Theory proposes that length contraction and time dilation are both real effects and observer effects—they are inseparable. According to Unified Field Theory, there is no fundamental distinction between real effects and observer effects. Physical concepts like space and time are descriptions created by observers and do not exist independently of them.

The unification of observer effect and real effect

The universe you perceive is the result of your brain processing and interpreting sensory inputs. Without an observer's description, physical phenomena such as color, heat, and sound cannot exist. In other words, the observer effect and the reality effect are not opposing concepts but two aspects of the same phenomenon. The brain's response to external stimuli—such as the perception of light or the sensation of heat—is not equivalent to the "true" existence of external phenomena; they are descriptions created by the brain to interpret external motion.

Unified Field Theory further proposes that the state of space is defined by its state of motion. Space is not static but moves at the speed of light. This motion is closely tied to the existence of observers—without an observer, the motion of space has no meaning. The three-dimensional orthogonal state of space arises from its continuous cylindrical spiral motion. This spatial state is geometrically equivalent to a physical state of motion, highlighting the intrinsic connection between space, motion, and observation.

The relationship between space motion and the observer

Unified Field Theory asserts that the motion of space is the observer’s description of the three-dimensional orthogonal state of space. The universe you perceive is not the "external" reality but rather the result of your brain’s processing and interpretation. For example, the red color you see is not an independent external entity but your brain’s perception and description of electromagnetic waves at a specific wavelength. Similarly, heat and sound are not external, independent "real" phenomena but descriptions of molecular motion and air vibrations as perceived by the observer.

Time and motion states are also descriptions made by the observer. When an object moves at the speed of light, its time ceases to flow, and the spatial length contracts to zero, giving the appearance that the object can "pass through" spatial barriers, such as walls. This phenomenon is not a fictional observer effect but a real result of the interaction between the object and the motion of space.

According to Unified Field Theory, an object’s mass and charge are proportional to the number of light-speed propagating lines in the space around it. As the object approaches the speed of light, the number of light-speed motion lines in its surrounding space decreases, leading to changes in the object’s mass.

The possibility of superluminal motion and unified field theory

According to Unified Field Theory, when an object’s mass approaches zero, it can move at the speed of light relative to an observer. At this point, the object’s mass and volume tend toward zero, enabling phenomena such as "passing through walls"—where the object traverses obstacles without any damage. Similar to the hypothetical alien spacecraft, an object moving at the speed of light is no longer constrained by the conventional limitations of time and space, making seemingly impossible phenomena achievable.

Unified Field Theory further suggests that as an object’s velocity approaches the speed of light, the space in the direction of motion undergoes compression, even tending toward zero. This compression effect can be explained geometrically through rotation: when an object moves at light speed along a particular axis, the spatial projection along that axis shrinks to zero, causing the object to occupy virtually no space.

Comparison between unified field theory and relativity

Although Unified Field Theory and Relativity may appear contradictory in some aspects, they are fundamentally unified. The length contraction and time dilation effects in Relativity are descriptions from the observer’s perspective under specific conditions. Unified Field Theory delves further into the physical background and mechanisms behind these phenomena. In Unified Field Theory, all physical phenomena—including mass, charge, energy, and force—are constructed through the observer’s description of the states of objects and space. Therefore, the observer effect and the reality effect are interdependent, without an absolute distinction.

Within the framework of Unified Field Theory, the existence of objects and space in the universe is independent of the observer. However, all other physical phenomena depend on the observer's description. This understanding provides a deeper worldview of physics, revealing the essence of physical quantities: they do not exist independently but are the result of the interaction between observers and the universe.

Explaining the constancy of the speed of light in relativity

Through the physical definition of time: Relativity is based on the invariance of the speed of light, but it does not delve into why the speed of light remains constant. Relativity assumes that the speed of light is constant in all reference frames, thereby extending and modifying Newtonian mechanics. It simply accepts the invariance of the speed of light as a fact and develops its theory upon this foundation, without providing the underlying mechanism for this invariance. Understanding why the speed of light is constant can begin with the physical definition of time.

In Unified Field Theory, the definition of time is directly related to the motion of space. According to this theory, the space surrounding any object (including the observer) disperses outward at the speed of light, c, from the point where the object is located. At the same time, light itself does not move relative to space but is "stationary" within space, propagating outward along with the motion of space. In other words, the time we perceive is essentially caused by the motion of space.

This motion of space creates a close relationship between time and spatial displacement. Specifically, time t is proportional to spatial displacement r: r = c∙t. This indicates that time and spatial displacement are physically unified, though we describe them separately.

The fundamental reason for the invariance of the speed of light

The speed of light is essentially the proportional relationship between spatial displacement and time t. According to the definition of a fraction, the numerator of the speed of light is the spatial displacement r, and the denominator is time t. In reality, spatial displacement and time are interdependent physical quantities, though we have artificially assigned them different names. Therefore, the spatial displacement and time in the definition of the speed of light are unified.

In other words, the reason the numerical value of the speed of light remains constant is that spatial displacement and time t, as a unified whole, change synchronously. If spatial displacement changes, time changes accordingly, ensuring that the speed of light remains constant.

Invariance of the speed of light in motion

When a light source is stationary relative to us or moving at a velocity v, the speed of light remains constant. Although the motion of the light source may affect the spatial displacement r, the proportional relationship between time t and spatial displacement ensures that t changes synchronously. As a result, the speed of light is unaffected by the motion of the light source and remains constant.

This reasoning reveals a core principle of General Relativity. General Relativity states that when two observers are in accelerated motion relative to each other, the speed of light observed by both remains the same. This implies that in mutually accelerating reference frames, the speed of light is identical for each observer.

Thus, the invariance of the speed of light is not merely a postulate of Relativity but stems from the intrinsic connection between space and time. Time and spatial displacement are interdependent physical quantities, and the speed of light, as the ratio between them, must remain constant. This principle provides a profound physical foundation for understanding the invariance of the speed of light and simultaneously validates the fundamental correctness of General Relativity.

Lorentz transformations in unified field theory

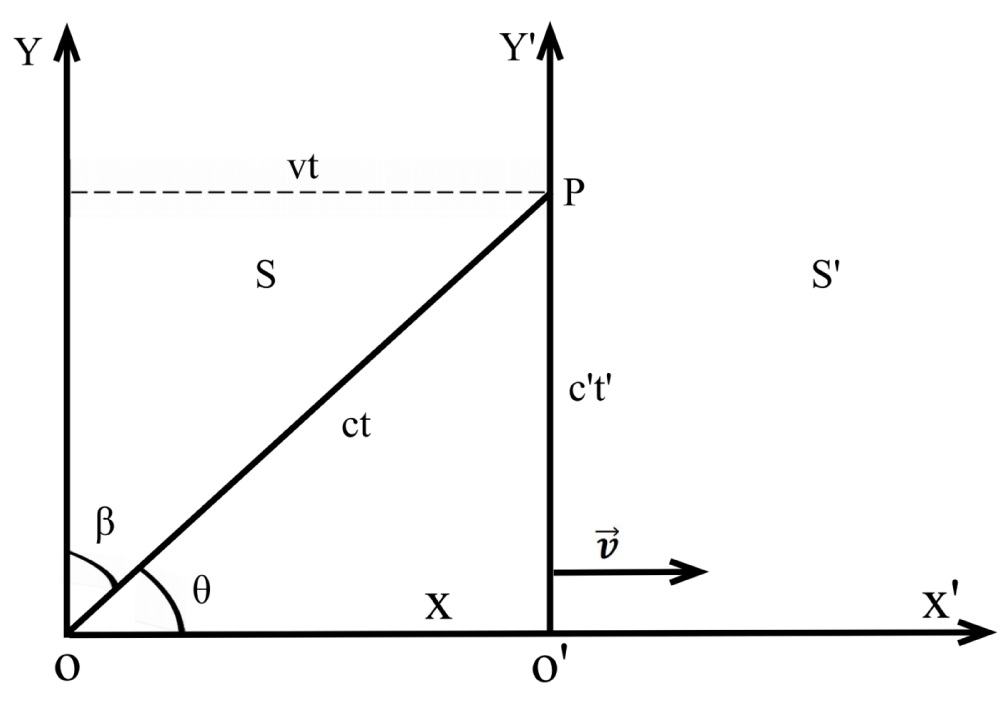
Explanation of the invariance of the speed of light in Lorentz transformation: Let there be two inertial Cartesian coordinate systems: S and S'. The spacetime coordinates of an arbitrary event occurring at point p(referred to as the observation point) are represented in S and S' as (x,y,z,t)and (x'', y',z',t'), respectively. This discussion focuses on the simplest case of the Lorentz transformation, where the observation point is stationary in the S' system (Figure 3).

The x-axis and x'-axis coincide, and at time t'=t=0, the origin o of the S-system (where the observer in S is located) and the origin o' of the S'-system (where the observer in S' is located) overlap. Subsequently, o moves relative to o with a constant velocity v along the positive direction of the x-axis. Imagine that at a certain moment, an explosion occurs. In the S'-system, the spatial and temporal coordinates of the explosion at point p are x', y,z', and t', respectively. This means the explosion occurs at time t', and point p, where the explosion takes place, is located at a distance x' from the origin o' along the x'-axis. Moreover, point P is stationary relative to S'. In the S-system, the spatial and temporal coordinates of the explosion at point p are x, y,z和t, respectively. This indicates the explosion occurs at time t, and point p is located at a distance x from the origin O along the x-axis. Additionally, point p moves with a velocity v relative to S. The task is to determine the relationship between the spacetime coordinates of the explosion event at point p in the two inertial reference frames. In Figure 3, it can be intuitively observed that:

$x^{\text{'}}=x-v t$

$x=x^{\text{'}}+v t^{\text{'}}$

According to the principle of Galilean relativity, the measurement of time and spatial length is independent of the observer's relative velocity v, allowing the above equation to hold, with t=t'. However, relativity posits that the measurement of time and spatial length depends on the relative velocity v between observers. As the velocity v increases, the spatial length contracts and becomes smaller. From the perspective of the observer in the S-system, the x’ in equation $\text{x'}=\text{x}-\text{v t}$ must be contracted by being multiplied by a relativistic factor 1/k, for the equation to hold. Thus, the relationship is given by:

$\frac{1}{k} x^{\text{'}}=x-v t$

Thus, we have:

$x\text{'}=k \left(x-v t\right)$ (1)

From the perspective of the observer in the S' system, the x in the equation $\text{x}=\text{x'}+\text{v t' }$ must be multiplied by a relativistic factor $\frac{1}{\text{k}}$ for the equation to hold. Thus, we have:

$\frac{1}{k} x=x\text{'}+v t\text{'}$

So there is:

$x=k (x\text{'}+v t\text{'})$ (2)

Since the S system moves relative to the S system in uniform linear motion, it is reasonable to assume that x’ and, as well as x and $(\text{x'}+\text{v t'}),$ have a linear relationship, satisfying a simple proportional relation.

The principle of relativity in relativity theory states that the laws of physics are identical or equivalent in all inertial reference frames. Therefore, the forms of physical equations should remain the same across different inertial frames.

Thus, equations (1) and (2) can include the same constant k. The value of k in the Lorentz transformation is determined by the invariance of the speed of light.

Imagine a beam of light emitted from the origin o and o', which are coincident at the initial time t=t'=0. The light propagates in the positive x-axis direction at a speed c.

Let the spacetime coordinates of the wavefront of the light beam (or the photon, or the spatial point p) be(x,y,z,t) in the S-system and (x', y,z',t') in the S'-system. We take the event of the wavefront of the light beam (or the photon, or the spatial point p) reaching its subsequent position as the object of our analysis.

If the speed of light c is the same in both the S system and the S' system, we have

$x=c t$ (3)

$x\text{'}=c t\text{'}$ (4)

Combining equations (1), (2), (3), and (4), we can derive:

$c t\text{'}=k (x-v t)$

$c t=k (x\text{'}+v t\text{'})$

Multiplying the two equations above, we can derive:

$c^2 t t^{\text{'}}=k^2 \left(x-v t\right) \left(x^{\text{'}}+v t^{\text{'}}\right)$

$=k^2 (x x^{\text{'}}+x v t^{\text{'}}-v t x^{\text{'}}-v^2 t t^{\text{'}})$

$=k^2 (x x^{\text{'}}+c t v t^{\text{'}}-v t c t^{\text{'}}-v^2 t t^{\text{'}})$

$=k^2 (c^2 t t^{\text{'}}-v^2 t t^{\text{'}})$

Deriving once again, we obtain:

$c^2=k^2 (c^2-v^2)$

$k=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$

Substituting the above equation into equations (1) and (2), we can obtain:

$x^{\text{'}}=\frac{x-v t}{\sqrt{1-\frac{v^2}{c^2}}}$ (5)

$x=\frac{x^{\text{'}}+v t^{\text{'}}}{\sqrt{1-\frac{v^2}{c^2}}}$ (6)

Eliminating x' using equations (5) and (6), we obtain:

$t^{\text{'}}=\frac{t-\frac{v x}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$ (7)

Eliminating x using equations (5) and (6), we obtain:

$t=\frac{t^{\text{'}}+\frac{v x^{\text{'}}}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$ (8)

The equation is:

$x^{\text{'}}=\frac{x-v t}{\sqrt{1-\frac{v^2}{c^2}}}$

$y^{\text{'}}=y$

$z^{\text{'}}=z$

$t^{\text{'}}=\frac{t-\frac{v x}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$

This is the Lorentz transformation in its standard form.

Equation:

$x=\frac{x^{\text{'}}+v t^{\text{'}}}{\sqrt{1-\frac{v^2}{c^2}}}$

$y=y^{\text{'}}$

$z=z^{\text{'}}$

$t=\frac{t^{\text{'}}+\frac{v x^{\text{'}}}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$

This is the Lorentz inverse transformation. Note that in the Lorentz transformation, y and z remain unchanged.

Now, using the physical definition of time, we explain the invariance of the speed of light in equations (3) and (4).

According to the previously established physical definition of time. In the system, the observer believes that a spatial point p(or the wavefront, or photon) departs from point o (or o, as o and o'coincide at zero time) at time t' = 0, traveling at the speed of light c along the positive x'-axis (or x-axis, as they coincide). After a duration t', it covers a distance x', reaching its subsequent position at point p. Thus, the relationship is: $\frac{{\text{x}}^{\text{'}}}{{\text{t}}^{\text{'}}}=\text{c}.$

In the S system, the observer believes that a spatial point p departs from point o (or o', as o and o' coincide at zero time) at time t = 0, traveling uniformly in a straight line along the positive x-axis (or x'-axis, as they coincide). After a duration t, it covers a distance x, reaching its subsequent position at point p.

The above physical definition of time tells us that time is proportional to the distance traveled by a spatial point in the space surrounding the observer. Thus, the time t in the S systemcompared to the time t' in the S' system, is equal to the ratio of the distance x traveled by the spatial point in the S' system. This can be expressed as:

$\frac{t}{t^{\text{'}}}=\frac{x}{x^{\text{'}}}$

By rearranging the above equation, we have:

$\frac{x}{t}=\frac{x^{\text{'}}}{t^{\text{'}}}$

Since x/ t and x'/t' both represent displacement over time (with the dimension of velocity), and both equal the speed of light c we have:

$\frac{x}{t}=\frac{x^{\text{'}}}{t^{\text{'}}}=c$

The above content indicates that there must exist a special velocity closely related to time, denoted as c. This velocity is observed to have the same value for two observers in relative motion. As long as the physical definition of time is correct, it can be proven that the speed of light c in the Lorentz transformation is constant and has the same value in both inertial reference frames.

Interpretation of Lorentz transformation through unified field theory

Inheritance and development of Lorentz transformation from galilean transformation: The Lorentz transformation builds upon the ideas of the Galilean transformation but introduces critical corrections. The Galilean transformation assumes that the spatial and temporal coordinates of the same event remain unchanged between two inertial reference frames S and S'. The Lorentz transformation, however, rejects this assumption. While it does not entirely negate the Galilean framework, it modifies and supplements it significantly. Specifically, in addressing changes in time and space, the Lorentz transformation shows that these are no longer absolute but depend on the observer’s state of motion.

Physical phenomena and observers in unified field theory: Unified Field Theory posits that all physical phenomena and forms of motion are described relative to an observer. Without the observer's description, discussing physical phenomena or states of motion is meaningless. It is always assumed that one of the reference frames, S or S', is the observer's frame of reference. Hence, any discussion of motion inherently relies on the observer's position and state. Without the observer's participation, physical concepts and quantities lack clear meaning.

Equality between reference frames: In Unified Field Theory, S and S' are considered two reference frames in relative motion. Importantly, any discussion of motion is inherently from the perspective of an observer in one of the frames. Although S and S' are in relative motion, there is no absolute standard for determining "who is moving." Motion is relative. It is usually assumed that one of the frames, S or S', is the observer’s frame, giving it a privileged role in describing physical phenomena. Only relative to this frame can physical quantities and events acquire clear physical meaning.

Four fundamental conditions for describing motion: Unified Field Theory asserts that any description of motion must satisfy four fundamental conditions: A. Space: The physical spatial coordinates where motion occurs. B. Time: The moments marking the start, progression, and end of the motion. C. Observer: The frame of reference describing the motion, typically the inertial frame in which the observer resides. D. Object Being Described: The entity or the event formed by the entity’s motion or changes.

These four conditions together form a complete description of any physical event. The definitions of space and time are inseparable from the observer’s existence; only through the observer’s description can physical phenomena have a definite physical meaning. Without one of these four conditions, the description of motion is incomplete and meaningless.

Unified Field Theory offers a new perspective on the Lorentz transformation. It not only inherits some ideas from the Galilean transformation but also makes significant modifications, particularly regarding the relativity of time and space. Within the framework of Unified Field Theory, we can understand the fundamental reason for the constancy of the speed of light and further recognize that motion, time, and space are, in essence, descriptions made by the observer.

Further analysis of unified field theory and Lorentz transformation

In specific cases, describing the motion of ourselves as observers is no different from describing the motion of external objects or events; the two can be considered the same subject. However, such a description is meaningful only in certain specific contexts; in general, it lacks significance. Unified Field Theory emphasizes that space itself is in motion, but merely describing the motion of space alone holds no practical meaning.

The motion of space must be referenced to a specific object or event. Without such a reference point, a description of spatial motion cannot be established. Therefore, when describing the motion of space, it is essential to clearly define an object or event as the basis for the description.

Key elements in Lorentz transformation

When applying the Lorentz transformation, the following conditions must be met: A. Identifying the Observer: Any physical description must first establish the observer’s frame of reference. Without the observer’s frame of reference, the description of physical phenomena or states of motion is meaningless. B. Defining the Object of Description: The described object can be a physical entity or an event arising from the motion of such an entity. These events must have a clearly defined starting point, progression, and endpoint in time, as well as a specific spatial location. C. Avoiding Confusion: Once the observer and the object of description are established, it is essential to clearly define the event’s spatial and temporal coordinates. Without these basic definitions, conceptual confusion is likely to arise.

Definition of relative motion and the distinction between static and moving frames

In Unified Field Theory, although there is no absolute state of motion, the definition of motion is always relative. Motion must be defined concerning a specific observer to have meaning. The conventional approach distinguishes as follows: A. S'-System (Moving Frame): The reference frame in which the described object or event resides is usually referred to as the "moving frame." In the S'-system, the object or event is considered to be in motion. B. S-System (Static Frame): The "static frame" refers to the reference frame that is stationary relative to the moving frame. In the S-system, the described object or event is perceived as at rest relative to the observer. Some argue that in the absence of a clearly defined baseline, a third reference frame (such as the Earth's surface frame) must be introduced to compare S and S' to determine which is the moving frame and which is the static frame. However, within the framework of Unified Field Theory, this approach is unnecessary. The observer's reference frame is always assumed to be absolute, as the frame in which the observer resides is unique. Therefore, the distinction between moving and static frames can be made directly without the need to introduce an external third reference frame for comparison.

Practical applications of Lorentz transformation

Lorentz forward transformation: When the observer is assumed to be in the static frame S, while the observed object or point p is in motion relative to the observer, the Lorentz forward transformation is used for coordinate conversion.

Lorentz inverse transformation: When the observer is assumed to be in the moving frame S', while the observed object or point p is stationary relative to the observer, the Lorentz inverse transformation is applied.

In both scenarios, the Lorentz transformation equations enable accurate conversion between reference frames while maintaining the consistency of physical laws across different frames. This reflects a core principle of Unified Field Theory: all physical phenomena are relative, and only by clearly defining the observer's reference frame can physical quantities have meaningful interpretations.

Unified Field Theory emphasizes the crucial role of the observer, offering a more comprehensive and consistent framework for understanding Lorentz transformations and their applications. By clearly defining the observer, the described object, and the temporal and spatial coordinates of events, Unified Field Theory avoids ambiguity in physical descriptions. It deepens our understanding of motion and time by reinforcing the idea that in Lorentz transformations, motion is always relative. All physical quantities and events must be described concerning a specific observer.

Insights on spacetime intervals and light invariance

Equivalence of time and space: In Unified Field Theory, time is regarded as the manifestation of the motion of space surrounding an object. In other words, moving space and time are equivalent. To ensure the physical equivalence of these two quantities, a constant must be introduced to maintain dimensional consistency. This constant is the speed of light, c. Thus, the displacement of moving space r can be expressed as: r=c•t, where time t and spatial displacement r are connected through the speed of light c. The introduction of c as a constant ensures that the motion of time and space is physically correlated and dimensionally consistent.

From a mathematical standpoint, the derivative of a variable concerning itself is typically 1 or a constant. Given that time t and spatial displacement r are linked by the speed of light c, their relationship is physically fixed. Thus, c, as a constant, does not change with variations in time or space.

The invariance of the speed of light in perpendicular directions of motion

Many may question how light can propagate in any direction if space itself moves. Does this mean that space must also move in all directions? Unified Field Theory explains this phenomenon: the motion of space is relative to the object it surrounds. Specifically, the space surrounding an object radiates outward from the object as its center.

In the absence of an object, describing the motion of space alone is meaningless. The motion of space must be referenced to something, and this reference is typically the object itself. Therefore, the motion of space is always relative to a specific object or observer.

We consider how to explain the invariance of the speed of light when the direction of light propagation is perpendicular to the velocity v of an object. Imagine the following scenario: A. There are two two-dimensional Cartesian coordinate systems, S and S'. B. At t' =t=0, the origins of S and S' coincide. C. Afterward, the S'-system moves relative to the S-system along the x-axis at a constant velocity v. In this setup, the observer in S is located at point o (the origin of S), while the observer in S' is at point o (the origin of S'). Since the motion of space is relative to the object, the speed of light remains constant (c) in all directions. Even when the observer and the light source are in relative motion, the speed of light is still c, consistent with the principles of the Lorentz transformation.

Why the speed of light is constant in a single reference frame

A key question remains: Why is the speed of light constant within a single reference frame? This can be understood as follows: time is entirely equivalent to the motion of space surrounding the observer, expressed as: Motion of space=Time.

To ensure this equivalence is dimensionally consistent in physics, a constant that does not vary with time or the motion of space must be introduced—this constant is the speed of light. Thus, the relationship becomes: Motion of space and Time.

From a mathematical perspective, taking the derivative of a variable concerning itself results in either 1 or a constant. Similarly, the constancy of the speed of light reflects this principle, ensuring the dimensional and conceptual consistency of the relationship between space and time.

Explanation of the invariance of the speed of light when the motion of a spatial point is perpendicular to the velocity v

Some may wonder: If light can propagate in any direction, doesn’t that mean space also moves in all directions? And what is the reference for the motion of space? According to Unified Field Theory, the space surrounding an object radiates outward with the object as its center.

The motion of space is always referenced to the object itself. Descriptions of spatial motion pertain to how the space around a specific object behaves. In special cases where no object is present, the motion of space is described relative to the observer’s body. Without any object, describing the motion of space alone is meaningless.

Now, let us consider the case where the motion of a spatial point is perpendicular to the velocity v of the observed object.

In Figure 4, the x-axis and x'-axis coincide. At t =t=0, the origin of the two-dimensional Cartesian coordinate system S (where the observer in S is located) overlaps with the origin O of the Cartesian coordinate system S' (where the observer in S' is located). Subsequently, the point O' moves relative to O at a constant velocity v (with magnitude v) along the positive x-axis.

Imagine a particle that remains stationary at the origin of the two-dimensional Cartesian coordinate system S'.

At the initial moment (t'=0), the observer in the S'-system, using the physical definition of time, observes a spatial point p departing from o'. Within a duration of t', the point p travels a distance o'p at the speed of light c along the y'-axis. Thus, we have $\frac{{\text{O}}^{\text{'}}\text{P}}{{\text{t}}^{\text{'}}}=\text{c,}$ and ppp reaches its subsequent position, marked as point p in the figure.

From the perspective of the observer in the S-system, the event of the spatial point p departing at zero time and moving to point P involves the point traveling a distance OP within a time t. While the distance OP is greater than O'P, the time t should also be longer than the time t'.

Because, according to the physical definition of time, time is proportional to the distance traveled by the spatial point p relative to the observer. Thus, we have the equation:

$\frac{\text{OP}}{{\text{O}}^{\text{'}}\text{P}}=\frac{\text{t}}{{\text{t}}^{\text{'}}}$

Rearranging the above equation, we get:

$\frac{OP}{t}=\frac{O^{\text{'}}P}{t^{\text{'}}}$

From $\frac{{\text{O}}^{\text{'}}\text{P}}{{\text{t}}^{\text{'}}}=\text{c},$ we obtain:

$\frac{OP}{t}=\frac{O^{\text{'}}P}{t^{\text{'}}}=c$

The above equation explains why the speed of light remains constant for two observers in relative motion. Next, we derive the relationship between t and t'to see if it aligns with the predictions of relativity. Starting from:

$\frac{OP}{t}=\frac{O^{\text{'}}P}{t^{\text{'}}}=c$

$OP=\sqrt{O^{\text{'}}{P}^2+v^2 t^2}$

From the given equation, we can derive:

$t^{\text{'}}=t \sqrt{1-\frac{v^2}{c^2}}$

The differential form can be obtained as:

$\frac{dt}{d{t}^{\text{'}}}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$

In relativity, it is assumed that for a particular event, the observer is stationary relative to the location where the event occurs. This means that the start and end times of the event are measured at the same location. The time measured for the duration of this event is called the proper time, which corresponds to t' in the equations above. In relativity, the proper time is the shortest time interval measured for an event. This result aligns perfectly with the predictions of relativity.

We apply the Lorentz inverse transformation.

$t=\frac{t^{\text{'}}+\frac{v x^{\text{'}}}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$

Taking the derivative of both sides concerning t', we get:

$\frac{dt}{d{t}^{\text{'}}}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$

Note that x' in the equation does not change with t', because both x' and t' are quantities observed in the S'-system. In the S'-system, the position of point p, x', remains stationary.

We apply the Lorentz forward transformation.

$t^{\text{'}}=\frac{t-\frac{v x}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$

Taking the derivative of both sides of the Lorentz forward transformation concerning t, we get:

$\frac{d{t}^{\text{'}}}{dt}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}-\frac{\frac{v^2}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$

$=\frac{1-\frac{v^2}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}$

$=\sqrt{1-\frac{v^2}{c^2}}$

Thus, we have:

$\frac{dt}{d{t}^{\text{'}}}=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$

Note that x represents the position of the point p in the S-system, which varies with time t. Thus, we have:

$\frac{dx}{dt}=v$

Additionally, we also have:

$\frac{d(\frac{v x}{c^2})}{dt}=\frac{v^2}{c^2}$

Since x and t are quantities observed in the S-system, and in the S-system, the position x of the point p is moving at a velocity v.

The relationship between the velocity of the light source $\overrightarrow{v}$ and the vector speed of light $\overrightarrow{c}$

In relativity, the speed of light is considered a constant, independent of the motion of the light source, the choice of observer, or the spatial or temporal position. Consequently, relativity does not delve into whether the speed of light can be treated as a vector and tends to regard it as a non-vector quantity. Within the framework of relativity, discussing the vector nature of the speed of light has no physical significance, as it is fundamentally a scalar constant.

The concept of the speed of light as a constant first appeared in Maxwell's electromagnetic wave equations, where the speed of light is consistently maintained as a constant within the equations.

Unlike relativity, Unified Field Theory proposes that the speed of light can, under certain conditions, be expressed as a vector. It suggests that the direction of the speed of light is functionally related to the velocity of the light source, thereby distinguishing between "scalar speed of light" and "vector speed of light." In this theory, the vector speed of light, denoted by $\overrightarrow{c}$ , has a constant magnitude but a variable direction, while the scalar speed of light, represented by c, remains invariant. The components of the vector speed of light along the x、y、, z axes are, and their magnitudes can change. However, because the scalar speed of light is constant, the sum of the squares of these components always equals c².

In Unified Field Theory, the relationship between the velocity of the light source $\overrightarrow{v}$ and the vector speed of light $\overrightarrow{c}$ is crucial. Let us first consider a special case where the angle between $\overrightarrow{c}$ and $\overrightarrow{v}$ is $\overrightarrow{V}$ We begin by roughly estimating the possible range of values for the scalar v and β. From relativity, we know that the invariance of the speed of light implies that v can induce changes in the component of the speed of light that is perpendicular to it, but it cannot affect the component of the speed of light that is parallel to $\overrightarrow{v}$ .

In Unified Field Theory, the change in $\overrightarrow{c}$ is solely a change in direction, while its magnitude remains constant. As $\overrightarrow{v}$ increases, the direction of $\overrightarrow{c}$ gradually deviates from its original position. When the deviation angle β is slightly greater than 0, it corresponds to v (the magnitude of $\overrightarrow{v}$ ) being slightly greater than 0. When β= = 90°, v equals the speed of light c. Thus, the value of β lies between 90°and 0°, while the magnitude of $\overrightarrow{v}$ , v, ranges from 0 to c (including c). Figure 4.

In the two-dimensional Cartesian coordinate systems S and S', the origins o and ' coincide at t=t'=0, with the x-axis and x' -axis also aligned. Subsequently, the S- and S'-systems move relative to each other in a straight line at a constant velocity $\overrightarrow{v}$ (with magnitude v) along the positive x-axis.

In this scenario, the particle o remains stationary at the origin o' of the S' -system. What we aim to examine is a spatial point p, which departs from oat zero time and moves along the y'-axis at the speed of light.

Description of light

In Unified Field Theory, light can be interpreted in different ways. If light is viewed as photons, the particle represents the light source, and point p represents a photon. If treated as a wave, point p corresponds to the position of the wavefront. However, a more general interpretation in Unified Field Theory views light as the excitation of electrons moving along with space. Even in the absence of excited electrons or photons—when a particle ceases to emit light and becomes an ordinary object—the surrounding space still expands outward at the vector speed of light $\overrightarrow{c}$ . In this case, point p can be considered a part of the space itself, representing a small region around point o.

Observer's perspective

From the perspective of the observer in the S'-system, point p departs from the particle at zero time and, after a duration t, reaches its subsequent position, having traveled a distance $\overrightarrow{\text{o'p}}=\overrightarrow{\text{c'}}\text{t'}$ at the vector speed of light.

From the perspective of the observer in the S-system, point p starts at zero time and travels a distance op = ct, at the vector speed of light $\overrightarrow{c}$ (with a magnitude of c) over the time t.

From Figure 4, it can be observed that:

$\frac{\left|\overrightarrow{v} t\right|}{\left|\overrightarrow{c}t\right|}=sin\text{β}=\frac{v}{c}$

Eliminating t, we can derive:

$\frac{\left|\overrightarrow{v}\right|}{\left|\overrightarrow{c}\right|}=sin\text{β}=\frac{v}{c}$

Since the angle between $\overrightarrow{c}$ and $\overrightarrow{v}$ is $\theta =\frac{\pi }{2}-\beta ,$ we have:

$\cos \theta =\frac{\left|\overrightarrow{v}\right|}{\left|\overrightarrow{c}\right|}=\frac{v}{c}$

From the above equation, we can derive:

$sin\theta =\sqrt{1-\frac{v^2}{c^2}}$

This is, in fact, the underlying reason for the emergence of the relativistic factor. From the above analysis, the following conclusions can be drawn: When the magnitude of $\overrightarrow{v}$ , v, approaches zero, and the initial state of $\overrightarrow{v}$ is perpendicular to the vector speed of light $\overrightarrow{c}$ , as v gradually increases, $\overrightarrow{c}$ will slowly deviate from its original position. When v approaches the magnitude of the speed of light c, $\overrightarrow{c}$ will have deviated by 90 degrees.

The motion of the light source at velocity $\overrightarrow{v}$ can cause the direction of the vector speed of light $\overrightarrow{c}$ to deflect in the direction perpendicular to $\overrightarrow{v}$ . This phenomenon can also be explained using the inverse of the perpendicular principle discussed earlier. The perpendicular principle tells us that the perpendicular state of space (90-degree angles) can lead to motion. Its inverse theorem states: motion can, in turn, cause the perpendicular state of space to tilt. When the velocity of motion reaches the speed of light, the perpendicular state completely vanishes (becomes flat).

The above formulas, $\text{sinβ}=\frac{\text{v}}{\text{c}}$ or $\text{cosθ}=\frac{\text{v}}{\text{c}}$ can be regarded as a quantitative analysis of the perpendicular principle.

The essence of the perpendicular principle is the equivalence and complementarity between spatial angles and motion velocity. The analysis above only examines the specific relationship between the vector speed of light $\overrightarrow{c}$ and the velocity of the light source $\overrightarrow{v}$ (with magnitude v). To uncover their general relationship, it is necessary to study the transformation of $\overrightarrow{c}$ between the inertial frames S' and S. In S', the three components of the vector speed of light $\overrightarrow{c\text{'}}$ are: $\overrightarrow{c_z^{\text{'}}}$ . In S, the three components of the vector speed of light $\overrightarrow{c}$ are: $\overrightarrow{c^{\text{'}}}$

Using the relativistic velocity transformation (which we have established as derived from the Lorentz transformation and thus valid), the three components of $\overrightarrow{{\text{c}}^{\text{'}}}$ and $\overrightarrow{c}$ satisfy the following relationships:

$c_x^{\text{'}}=\frac{c_x-v}{1-\frac{c_x v}{c^2}}$

$c_y^{\text{'}}=\frac{ c_y \sqrt{1-\frac{v^2}{c^2}}}{1-\frac{c_x v}{c^2}}$

$c_z^{\text{'}}=\frac{ c_z \sqrt{1-\frac{v^2}{c^2}}}{1-\frac{c_x v}{c^2}}$

From the above equations, we can derive:

$c_x^{\text{'}}{}^2+c_y^{\text{'}}{}^2+c_z^{\text{'}}{}^2$

$=\frac{{(c_x-v)}^2+c_y{}^2 (1-\frac{v^2}{c^2})+c_z{}^2 (1-\frac{v^2}{c^2})}{{(1-\frac{c_x v}{c^2})}^2}$

$=\frac{c^4 [c_x{}^2+c_y{}^2+c_z{}^2-2 c_x v+v^2-\left(c_y{}^2+c_z{}^2\right) \frac{v^2}{c^2}]}{{(c^2-c_x v)}^2}$

$=\frac{c^4 [c^2-2 c_x v+v^2-\left(c^2-c_x{}^2\right) \frac{v^2}{c^2}]}{{(c^2-c_x v)}^2}$

$=\frac{c^4 (c^2-2 c_x v+\frac{c_x{}^2 v^2}{c^2})}{{(c^2-c_x v)}^2}$

$=\frac{c^2 (c^4-2 c^2 c_x v+c_x{}^2 v^2)}{{(c^2-c_x v)}^2}$

$=c^2$

From this, we can derive the relationship that the vector speeds of light $\overrightarrow{c}$ and $\overrightarrow{c^{\text{'}}}$ satisfy: $\overrightarrow{c^{\text{'}}}\cdot \overrightarrow{c^{\text{'}}}=\overrightarrow{c}\cdot \overrightarrow{c}=c^2.$ The directions of $\overrightarrow{c}$ and $\overrightarrow{c^{\text{'}}}$ are different, but their magnitudes are the same.

To derive the invariance of spacetime intervals in relativity

Let us consider two observers, one in the S-system [with spacetime coordinates (x,y,z,t)] and the other in the S'-system [with spacetime coordinates (x', y, z', t')]. The S-system moves relative to the S'-system at a constant velocity V along the positive x-axis.

At time t = t' 0, the origins o of the S-system and o of the S'-system coincide. A spatial point p starts at time 0 from o and o', and after some time, it reaches its current position.

Transform the equation: $\overrightarrow{r}\left(t\right)=\overrightarrow{c} t=x \overrightarrow{i}+y \overrightarrow{j}+z \overrightarrow{k}.$ Taking the dot product of the equation with itself, the result is: $r^2=c^2 t^2=x^2+y^2+z^2.$ R is the magnitude of the vector $\overrightarrow{r}.$ It represents the distance measured by an observer in the S-system, indicating the displacement of the spatial point relative to the origin. The above equation also appears in relativity, where it is interpreted as the four-dimensional spacetime interval.

Similarly, the displacement of point p relative to o' as measured by an observer in the S'-system can be expressed as: ${\text{r}}^{\text{'}}{}^2={\text{c}}^2{\text{ t}}^{\text{'}}{}^2={\text{x}}^{\text{'}}{}^2+{\text{y}}^{\text{'}}{}^2+{\text{z}}^{\text{'}}{}^2.$ From ${\text{r}}^2={\text{c}}^2{\text{ t}}^2={\text{x}}^2+{\text{y}}^2+{\text{z}}^2,$ we can derive: ${\text{c}}^2{\text{ t}}^2-\left({\text{x}}^2+{\text{y}}^2+{\text{z}}^2\right)=0,$ From ${\text{r}}^{\text{'}}{}^2={\text{c}}^2{\text{ t}}^{\text{'}}{}^2={\text{x}}^{\text{'}}{}^2+{\text{y}}^{\text{'}}{}^2+{\text{z}}^{\text{'}}{}^2,$ we can derive: $c^2 t^{\text{'}}{}^2-\left(x^{\text{'}}{}^2+y^{\text{'}}{}^2+z^{\text{'}}{}^2\right)=0.$

From the above equation, it can be concluded that the spacetime interval remains invariant in two inertial frames undergoing relative uniform linear motion. Unified Field Theory interprets this invariance of the spacetime interval as a manifestation of spacetime unification, where time is fundamentally the result of space moving at the speed of light.

Future perspectives: Artificial intelligence and spiral space‑time

Recent advances in Artificial Intelligence (AI) have transformed how physicists interrogate complex, data‑rich systems — from gravitational‑wave catalogs to deep‑sky surveys. Within the UFT framework, AI can accelerate progress along two fronts. (1) Theory discovery. Symbolic‑regression and large‑language‑model tools can sift through high‑dimensional simulations of spiral space‑time to suggest new conservation principles or hidden symmetries that elude manual derivation. (2) Mission design and data reduction. Reinforcement‑learning navigators trained on UFT‑consistent gravitational maps could optimise low‑energy transfer orbits, while graph‑neural networks can identify subtle correlations between spacecraft telemetry and local space‑time curvature. By treating AI as a hypothesis‑generating partner rather than a mere calculator, future researchers may expose deeper layers of the spiral‑motion paradigm and design experimental tests—both terrestrial and extra‑planetary—that were previously impractical. This outlook positions AI as a catalyst for turning UFT’s conceptual unification into predictive, testable science.

This study advances a concept‑centred Unified Field Theory (UFT) by explicitly redefining space as a continuously spiralling continuum, time as the observer’s perception of that motion, and motion itself as the interplay between objects moving through space and space moving itself. On this foundation, we propose that every physical phenomenon—mass, charge, energy, and even the four fundamental forces—emerges from spatial displacement traced along a right‑handed cylindrical spiral that propagates at the speed of light.

The spiral‑space model coherently reinterprets gravitational, electromagnetic, weak‑nuclear, and strong‑nuclear interactions as different observational facets of the same underlying kinematics. Because time is defined by the outward motion of space, the constancy of the speed of light becomes a natural corollary, and relativistic effects such as time dilation and length contraction follow without additional postulates. Revisiting Lorentz transformations under this lens preserves their mathematical form while offering a clearer physical rationale rooted in the autonomous motion of space.

Beyond its theoretical unity, UFT is forward‑looking. Recent developments in Artificial Intelligence—symbolic regression, physics‑informed neural networks, and reinforcement‑learning mission planners—can now be mapped onto spiral space‑time dynamics, providing powerful tools to uncover hidden symmetries and design energy‑efficient deep‑space trajectories.

By unifying foundational concepts while inviting AI‑driven exploration, this work lays conceptual and methodological groundwork for the next generation of space‑time research and challenges conventional boundaries in our quest to understand the cosmos.

Authors’ contributions

X.Z. Conceptualized the study, developed the methodology, and wrote the original draft. P.Z. supervised the project and reviewed and edited the manuscript. All authors reviewed the manuscript.

Acknowledgement

We would like to express our sincere gratitude to everyone involved in this research work.

Declaration of competing interest

The authors unequivocally declare the absence of any competing interests or conflicts of interest.

Data availability

The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.

1. Kim S, Schwenk J, Walkup D, Zeng Y, Ghahari F, Le ST, et al. Edge channels of broken-symmetry quantum Hall states in graphene visualized by atomic force microscopy. Nature Communications. 2021;12(1):2852. Available from: https://doi.org/10.1038/s41467-021-22886-7
2. Young AF, Sanchez-Yamagishi JD, Hunt B, Choi SH, Watanabe K, Taniguchi T, et al. Tunable symmetry breaking and helical edge transport in a graphene quantum spin Hall state. Nature. 2014;505(7484):528–32. Available from: https://doi.org/10.1038/nature12800
3. Yao W, Yang SA, Niu Q. Edge states in graphene: From gapped flat-band to gapless chiral modes. Physical Review Letters. 2009;102(9):096801. Available from: https://doi.org/10.1103/PhysRevLett.102.096801
4. Plotnik Y, Rechtsman MC, Song D, Heinrich M, Zeuner JM, Nolte S, et al. Observation of unconventional edge states in “photonic graphene”. Nature Materials. 2014;13(1):57–62. Available from: https://doi.org/10.1038/nmat3783
5. Xu B-C, Xie B-Y, Xu L-H, Deng M, Chen W, Wei H, et al. Topological Landau–Zener nanophotonic circuits. Advanced Photonics. 2023;5(3):036005. Available from: https://doi.org/10.1117/1.AP.5.3.036005
6. Wang H, Cao Q, Peng Q, Liu S. Atomistic study of mechanical behaviors of carbon honeycombs. Nanomaterials. 2019;9(1):109. Available from: https://doi.org/10.3390/nano9010109
7. Sang M, Shin J, Kim K, Yu KJ. Electronic and thermal properties of graphene and recent advances in graphene-based electronics applications. Nanomaterials. 2019;9(3):374. Available from: https://doi.org/10.3390/nano9030374
8. Sepehri A, Ghassem-Alaskari MK. The Feasibility of Synthesized Micro Graphene Particles. 9th International Conference on Research in Science and Engineering, KBU, Bangkok, Thailand, EN-P-543. 2025.
9. Wang J, Mu X, Sun M. The thermal, electrical, and thermoelectric properties of graphene nanomaterials. Nanomaterials. 2019;9(2):218. Available from: https://doi.org/10.3390/nano9020218
10. Semenoff GW. Condensed-matter simulation of a three-dimensional anomaly. Physical Review Letters. 1984;53(26):2449–52. Available from: https://doi.org/10.1103/PhysRevLett.53.2449
11. Wallace PR. The band theory of graphite. Physical Review. 1947;71(9):622–34. Available from: https://doi.org/10.1103/PhysRev.71.622
12. Lamas CA, Cabra DC, Grandi N. Generalized Pomeranchuk instabilities in graphene. Physical Review B. 2009;80(7):075108. Available from: https://doi.org/10.1103/PhysRevB.80.075108
13. Fuhrer MS. Critical mass in graphene. Science. 2013;340(6139):1413–4. Available from: https://doi.org/10.1126/science.1240317
14. Charlier J-C, Eklund PC, Zhu J, Ferrari AC. Electron and phonon properties of graphene: Their relationship with carbon nanotubes. In: Jorio A, Dresselhaus G, Dresselhaus MS, editors. Carbon Nanotubes: Advanced Topics in the Synthesis, Structure, Properties and Applications. Springer-Verlag; 2008.
15. Morozov SV, Novoselov K, Katsnelson M, Schedin F, Elias D, Jaszczak J, Geim A. Giant intrinsic carrier mobilities in graphene and its bilayer. Physical Review Letters. 2008;100(1):016602. Available from: https://doi.org/10.1103/PhysRevLett.100.016602
16. Chen JH, Jang C, Xiao S, Ishigami M, Fuhrer MS. Intrinsic and extrinsic performance limits of graphene devices on SiO₂. Nature Nanotechnology. 2008;3(4):206–9. Available from: https://doi.org/10.1038/nnano.2008.58
17. Kusmartsev FV, Wu WM, Pierpoint MP, Yung KC. Application of graphene within optoelectronic devices and transistors. arXiv preprint, arXiv:1406.0809. 2014. Available from: https://arxiv.org/abs/1406.0809
18. Neto AHC, Peres NMR, Novoselov KS, Geim AK. The electronic properties of graphene. Reviews of Modern Physics. 2009;81(1):109–62. Available from: https://doi.org/10.1103/RevModPhys.81.109
19. Novoselov KS, Geim AK, Morozov SV, Jiang D, Katsnelson MI, Grigorieva IV, et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature. 2005;438(7065):197–200. Available from: https://doi.org/10.1038/nature04233
20. Tombros N, Jozsa C, Popinciuc M, Jonkman HT, van Wees BJ. Electronic spin transport and spin precession in single graphene layers at room temperature. Nature. 2007;448(7153):571–4. Available from: https://doi.org/10.1038/nature06037
21. Cho S, Chen Y-F, Fuhrer MS. Gate-tunable graphene spin valve. Applied Physics Letters. 2007;91(12):123105. Available from: https://doi.org/10.1063/1.2784934
22. Ohishi M, Shiraishi M, Nakanishi T, Suzuki Y. Spin injection into a graphene thin film at room temperature. Japanese Journal of Applied Physics. 2007;46(25):L605–7. Available from: https://doi.org/10.1143/JJAP.46.L605
23. Borghino D. Liquid-like graphene could be the key to understanding black holes. New Atlas. 2016 Feb 15. Available from: https://newatlas.com/liquid-graphene-dirac-fluid/41801/
24. Hashimoto T, Kamikawa S, Yagi Y, Haruyama J, Yang H, Chshiev M. Graphene edge spins: Spintronics and magnetism in graphene nanomeshes. Nanosystems: Physics, Chemistry, Mathematics. 2014;5(1):25–38. Available from: https://nanojournal.ifmo.ru/en/wp-content/uploads/2014/02/NPCM51_P25-38.pdf
25. Bolotin KI, Ghahari F, Shulman MD, Stormer HL, Kim P. Observation of the fractional quantum Hall effect in graphene. Nature. 2009;462(7270):196–9. Available from: https://doi.org/10.1038/nature08582
26. Gusynin VP, Sharapov SG. Unconventional integer quantum Hall effect in graphene. Physical Review Letters. 2005;95(14):146801. Available from: https://doi.org/10.1103/PhysRevLett.95.146801
27. Zhang Y, Tan Y-W, Stormer HL, Kim P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature. 2005;438(7065):201–4. Available from: https://doi.org/10.1038/nature04235
28. Kim M, Hwang HM, Park GH, Lee H. Graphene-based composite electrodes for electrochemical energy storage devices: Recent progress and challenges. FlatChem. 2017;6:48–76. Available from: https://doi.org/10.1016/j.flatc.2017.08.002
29. Ghassem-Alaskari MK, Sepehri A, Kassaee MZ. Unlocking Graphene’s Potential: Size Distribution and Topological Advances. International Journal of Physics Research and Application. 2025. Available from: https://doi.org/10.1016/j.jics.2024.101173
30. Le Ferrand H, Chabi S, Agarwala S. 3D assembly of graphene nanomaterials for advanced electronics. Advanced Intelligent Systems. 2020;2(5):1900151. Available from: https://doi.org/10.1002/aisy.201900151
31. Yan Z, Nika DL, Balandin AA. Thermal properties of graphene and few-layer graphene: Applications in electronics. IET Circuits, Devices & Systems. 2015;9(1):4–12. Available from: https://doi.org/10.1049/iet-cds.2014.0093
32. Binnig G, Quate CF, Gerber C. Atomic force microscope. Physical Review Letters. 1986;56(9):930–3. Available from: https://doi.org/10.1103/PhysRevLett.56.930
33. Kim CJ, Sánchez-Castillo A, Ziegler Z, Ogawa Y, Noguez C, Park J. Chiral atomically thin films. Nat Nanotechnol. 2016;11(6):520–4. Available from: https://doi.org/10.1038/nnano.2016.3