More Information
Submitted: September 21, 2025 | Approved: October 01, 2025 | Published: October 01, 2025
How to cite this article: Holubets TV. The Modelling of Dielectric Relaxation under Microwave Treatment into Porous, Humidified Body. Int J Phys Res Appl. 2025; 8(10): 288-299. Available from:
https://dx.doi.org/10.29328/journal.ijpra.1001138
DOI: 10.29328/journal.ijpra.1001138
Copyright license: © 2025 Holubets TV. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is propeRLy cited.
Keywords: Porous media; Microwave treatment; Polarization; Pulse relaxation method; Equations of electromagnetic field; Dielectric relaxation; Dielectric loss factor; Effective dielectric constant; Wave processes; Refractions and transmission; Boundary problem
The Modelling of Dielectric Relaxation under Microwave Treatment into Porous, Humidified Body
Taras Volodymyrovych Holubets*
Prodi of Physics, University of Indonesia, 40122, Indonesia
*Address for Correspondence: Taras Volodymyrovych Holubets, Department of Physico-Mechanical Fields: Pidstryhach Institute for Applied Problems of Mechanics and Mathematics of NAS Ukraine, Naukova Street 3-b, 79060, Lviv, Ukraine, Email: [email protected]
According to the method of local special averaging, a porous medium is considered as a continuum of material points with averaged or effective physical properties. The equations of electrodynamics are written in the reduced form by the definition of the generalized dielectric constant. To describe the dielectric properties of a modelled three-phase porous medium, the possibility of using the pulse relaxation method is demonstrated. Based on the dielectric properties by the using of pulse relaxation function, the polarization and current via delay functions are defined depending on the volume fraction of the saturation of the porous medium with liquid phases. The time limits of the proposed relaxation functions are analysed and in the harmonic approximation of the field amplitudes, a transparent expression for the generalized dielectric displacement vector is written in terms of physical content. Within the framework of the effective macroscopic field approximation according to the cluster approach, a method of averaging local equations of the electromagnetic field is demonstrated. The generalized complex dynamic dielectric constant for the composite porous body is determined. The compatibility conditions of the demonstrated method for describing of electromagnetic processes in a heterogeneous multiphase porous medium are recorded.
We are considering the porous three-phase medium, as composite material, which is characterized by the low conductivity. This is a composite body of low electro-conductivity (C.B.L.C.) (not ideal dielectric [1]). The low electrical conductivity of such body in general is conditioned with conductive properties of water (liquid phase). In general the energy dissipation of the external microwave electromagnetic field (E.M.F.) can be caused by the charged particles during own oscillation or orientations movements: , this is the dielectric losses (polarization heat release), here Pv is the power of heat releasing into body on the unity of the volume, k is the dimension constant, E and f are the stretch a frequency of electric field, and are the real and imaginary parts of the dielectric constant, tgδ is the tangent of dielectric loss, so and dissipation of energy by the charge carries (free electrons or ions): Pv = E2qnµ, this is Joule's heat releases (ionic conductivity), here E - is the electric field stretch, q is the electric charge of each of ions, and n and µ are concentration and mobility of ions correspondingly.
In the future corresponding to the effective macroscopic field under harmonically approach of E.M.F. we will be modelling the polarization heat releases which are causes by the dielectric losses from the side of hard matrix (carcass or skeleton) and free (not joined or not adsorbed) water. We will review the humidified air as not conductive media. The joules heat releases because of ions and electrons conductivity of liquid phase (water) we are neglectedor bypassed.
The local space averaging
The three-phase macroscopic porous area, volume or cell P of the humidified porous body, as it was mentioned into work [2], consist from the solid PS, liquid PL and gas PG, so arbitrary volume of averaging ΔVR contains the phases sub volumes for skeleton (solid phase), water ∆VL(t) (liquid phase) and gas ∆VG(t) (this is mixture of dry air a and water vapor v components), which may to changes with time t. Through the sub volumes ∆VL(t) and ∆VG(t) we can defines the volume of pores ∆VP(t)=∆VL(t)∪∆VG(t) under condition , where σ = {S,L,G} is the index of phase.
The configuration and displacement of phases into the averaging volume of the body can be rewritten with usage of this characteristics function
(1)
This function also takes into account the time moving of phases for considering body, which can be conditioned by the mass transfer processes or the mechanical deformations. So, , and volume of σ-phase of the material can be determined as
(2)
here and t are denotes the coordinate and time into the mezoscopic scale [2] accordingly.
Also we can review the physical quantities of the pore saturations by the liquid ηl or the gas ηg correspondingly
(3)
Then, according to the known volumetric definition [3] of the local porosity
(4)
the volume fractions of phases are satisfy the following relations
(5)
Let's define through the function into ranges of R.E.V. (the Representative Averaging Volume [4]) a certain the local value of any physical quantity, which characterize the macroscopic physical volume P of the considering porous body. The space averaging of such quantity in the point of the macroscopic porous volume into the time moment t determines [3] in the such way
. (6)
Similarly, by the usage of the characteristic function (1), we may reproduce [2] the phase
(7)
and internal
(8)
as an averaged quantities.
Because the relation is satisfy
the phase and internal averaged are interconnected
So, using the method of the local spatial averaging, a reviewed heterogeneous porous cell P can be described under certain continuous by the local physical quantities in coordinate and time space. This makes it possible to consider this one as the superposition of the three material continua: skeleton, liquid, and gas. With this approach, the equations for represented mathematical model of this porous cell can be written relatively to the specified average values (6-8) and are formally equivalents to the equations for a homogeneous (isotropic) single-phase cell according to the approximation of the model [4] for the continuous solid medium approach.
The equations of electrodynamics
In the microwave electromagnetic field (E.M.F.) frequency range according to the theory of dielectric relaxation Botcher-Bordewijk [5] we can review the vector of the generalized dielectric displacement by the known relation(9)
Where is the vector of dielectric displacement, which consider polarization processes into continuous media. Here and are the vectors of polarization and stretch of electric field, and is the density of polarization current.
From the condition of continuity it is following the expression for the density of polarization charge , according to this into the local averaging volume (R.E.V.) [2] the microscopic equations of E.M.F. Maxwell-Lorents into homogeneous form [6,7] and boundary conditions have the form
(10a)
where
(10b)
are the conditions of continuity for components and derivatives of the field. Here are denotations of phases, t and n are indexes, which define the tangential and normal components of field on the surfaces ∆Sσσ, of separations of phases accordingly. The system of equations (10a) is satisfied under conditions, that charges and currents of other nature into the investigated closed system are absent.
The operators of dielectric susceptibility and conductivity
The constitutive or material equations is proposed to write into following case
(11)
Where, and are operators of dielectric permeability, susceptibility and conductivity of cell correspondingly, ε0 and µ0 are dielectric and magnetic constants into vacuum respectively. It is important to note, that under conditions of absence of joules heat releasing at the fixed frequency of E.M.F. and absence of dispersion, into harmonic approximation of the field amplitudes (see Section 2, subsection 2 eqv. (28)) the operators of dielectric permeability and conductivity must have to satisfy the known [7] relation
(12)
where ω is the index, which point on the fixed frequency of harmonic field. Then the density of polarization current , here is the polarization vector, is determined in the usual way.
Let's define the operators of dielectric susceptibility x and conductivity σ of the considering media in the form of linear integration operators
and , (13)
where is an arbitrary continuous function of values for the coordinates and time. If and are local susceptibility and conductivity of medium, then and are pulse-relaxation functions [5], also and are the functions of delaying for polarization and current, which describe the reverse processes of relaxation for polarization and current accordingly.
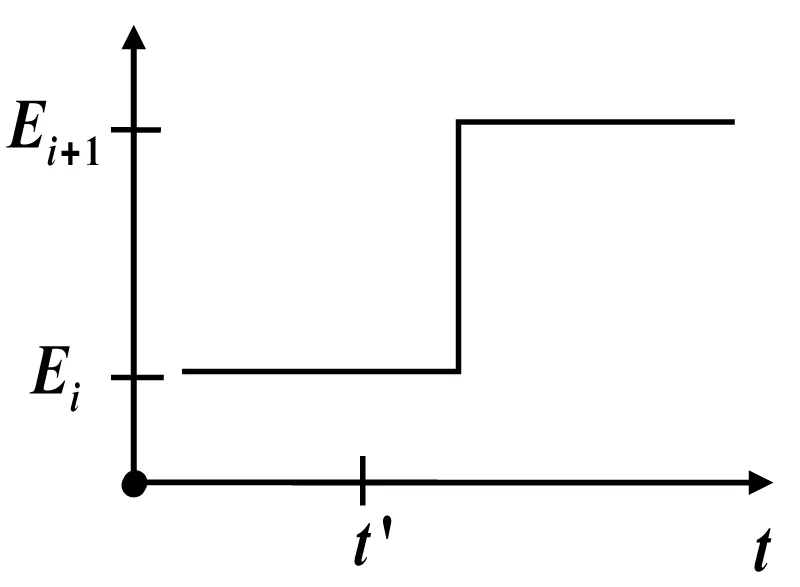
We are considering the linear homogeneous dielectric, for each point of which the principle of superposition of electromagnetic fields is satisfied. It is taking a possibility to modelling of time hopping (Figure 1) of electrical field into fixed point of investigated medium relatively to constant quantity of electric field stretch into ranges of σ-phase of porous material.
Figure 1: The quantities of polarization for -phase: , when and , when .
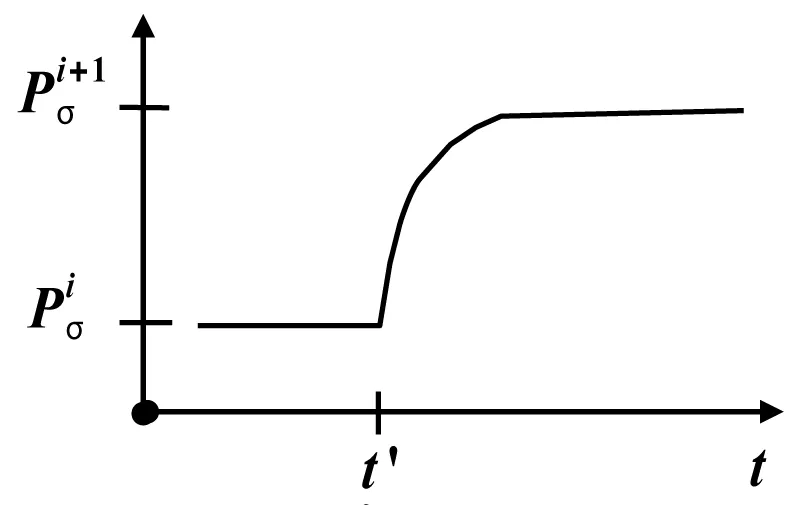
where is the theta-function of Heaviside [8]. Then the dielectric response of substance for σ-phase (Figure 2) can be defined by the relation
Figure 2: The quantities of electric field stretch Ei, when and when and and Ei+1, when .
, (14)
here is the stepped function of response for polarization, xσ is the static susceptibility of σ-phase.
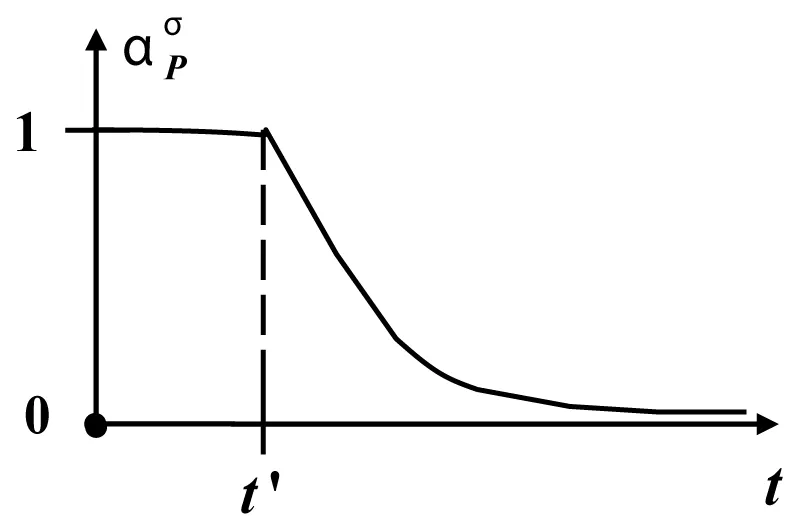
It should be noted, what defined abstractly the step response function of the polarization α for dielectric material of the σ-phase is displayed by the real function (Figure 3) of polarization delaying
Figure 3: The function of delaying of polarization for -phase.
Because , where is the time offset symbol, when at we get , and when we have , under executing [5] of a necessary condition of normalization.
In the case of the Debay`s type of relaxation [5] we receive the known classical relaxation relation
(15)
The local macroscopic field can be defined, as the superposition of amplitude-vector (coordinate) fields through the time step-impulse function in the interval at the arbitrary current t value of time
Then a vector of polarization for the medium of σ-phase the material have viewed
Under boundary limit ∆t → 0 with considering of material properties for σ-phase we get the expression for determining of polarization vector
(16)
here is the impulse-relaxation function for polarization of σ-phase.
Similarly by the mirroring of images Figures 1,2 relaying to averaged hope of electric field stretch and current along the abscissa axis and shifting for modulus per unit of current relaxation values (Figure 3) under inverse mapping along the axis we get the expression for determining of the polarization current vector for σ-phase of material
(17)
here is the impulse-relaxation function for σ-phase polarization current.
According to the local averaging method (see. Section 1, eqv. (6)) it is possible to define the averaged susceptibility and conductivity into the local volume of averaging in the such way
(18)
here xσ and σσ is the specific values of susceptibility and conductivity, and is the volume fraction of σ-phase correspondingly. Here the times of polarization and heat and mass exchanges processes t are separated because of the transience of polarization processes , where ω is the fixed so match frequency of E.M.F. under microwave irradiation) relatively to the slow temporal changes in the heat and mass transfer phenomena.
Into approach of local macroscopic field [4] the space averaged kernels of relaxation for susceptibility and current into range of [9] can rewrite (see also Appendix) through approximate expressions
Here, and , where is the index of conventional designation for vectors of polarization P and current J relatively, the impulse-relaxation functions and functions of response for polarization and current of σ-phase.
According to (16) and (17) under applying of local averaging method [9] we receive the averaged vectors of the orientational polarization
(19)
and the current of polarization into porous media
(20)
Here and is the static susceptibility and conductivity of σ-phase, which are interconnected through the known [6] relation
From the received expressions, the vectors of dielectric displacement and current into porous media take the form
(21)
where
(22)
and
(23)
Are corresponding impulse-relaxation functions and is the Dirace [8] delta function.
Then the functions of delaying for dielectric displacement and polarization current (see Appendix) have the view
(24)
(25)
where and are defined above averaged susceptibility and conductivity accordingly.
During receiving of expressions (22) and (23) for impulse-relaxation functions is taken into account the join (12) between the polarization and current vectors as well, as also reverse relatively to polarization similarity to the relaxation properties of current. According to the definition (9) of generalized displacement vector of σ-phase the material on the base of relations (16) and (17) it is follows
In the way of integration by parts of second application of sum from the definition of impulse-response function, it is follows
then
From this according to (19) with taking into account received expressions for impulse-response functions (22) and (23) it follows, that space averaged vector of generalized dielectric displacement can be defined in the such way
,
here RP and RJ are the relaxation products for polarization and current accordingly, which can be described by the following relations
, (26)
,(27)
here and are averaged according to the relation (18) susceptibility and conductivity of porous body.
With taking into account the known relation [6] for σ-phase under condition of executing of averaged material or constitutive equation
On the mezoscopic level of the space averaging [9] we're going to more transparent for the physical sense equation
here and are relaxation functions for polarization (24) and current (25), which needs to determine.
The harmonic approach of field amplitude
Into harmonic approach of electric and magnetic fields amplitudes
(28)
where are complex amplitudes, which light varying with the time t function due to moving of liquid phases into porous skeleton, according to the local view of equations E.M.F. (10a) the averaged (mezoscopic) equation are received
(29)
with corresponding material relations
(30)
where and are effective dynamical generalized and local complex dielectric constant (C.D.C.), is the local complex conductance.
Also
, (31)
are corresponding Laplace [8] images from averaged (22) and (23) relaxation functions.
Because , so real and imaginary part of generalized dynamic (C.D.P.) and takes the form
(32)
here is the effective-generalized complex dynamic dielectric constant (C.D.D.C.).
By the using of definition (9) of the generalized dielectric displacement vector and complex amplitudes (28) of field, the material equation (30) in the case of composite bodies with low electrical conductivity (C.B.L.C.) we can define trough relation
(33)
where is generalized complex dynamical dielectric constant (G.C.D.D.C.), and are the real and imaginary parts correspondingly.
Because the joules heat exchanges was missing or neglected, so takes and . According to the relation (30) into taken definitions, we receives
(34)
where real and imaginary part of generalized complex dynamic dielectric permittivity (G.C.D.D.P.) (33) have the view
(35)
here is the local complex dynamical constant.
Also according (28) the dispersion relation [10] are satisfied
(36)
here is the generalized complex dynamical dielectric constant (G.C.D.D.C.).
Under known material or constitutive relations for field equation (33) into (C.B.L.C.) relatively to complex amplitudes of E.M.F. (10a) we obtain in the following form
(37)
where is the generalized complex dynamical dielectric constant (G.C.D.D.C.), which is defined according to equation (35) under conditions of satisfied of dispersion (36) relations.
The space averaged equations of electromagnetic field
Because into multiphase porous cell electro-physical characteristics change like jumpy on the surface separation of two phases, so generalized complex (dynamical) dielectric permittivity (G.C.D.D.P.) can not be the continues function of coordinate. In general the last one can be defined by the characteristic (phase) function ϑσ (here σ = {S,L,G} is point to the index of phase), which is defined according to known relation (Section 1, eqv. (1), through this relation
(38)
where is the generalized complex dynamical dielectric constant (G.C.D.D.C.) for σ-phase (here σσ is the constant conductivity of σ-phase). Because of this the characteristics of field, which is included into the equations (37) of electrodynamics also will be stepping like functions of coordinate. For describe of the electromagnetic field in a porous cell P, as in the continuous medium approach by the continuous functions, we will use the methods of the theory of local spatial averaging [6]. For this purpose, we assume that the equations of electromagnetic field and material relations relative to the specified above the averaged (effective) quantities takes the same form as in the case of a single-phase (continuous) medium, i.e., they are formally equivalent. Formal equivalence of equations is ensured by fulfilling boundary conditions (10b) at the interface of two media on a microscopic scale at each (current) moment of time, and the formal equivalence of material relations is ensured by the definition of the effective electrophysical characteristics. Such effective characteristics are established within the averaging region Ω (R.E.V.) [2] and are determined through local properties of the environment based on certain geometric model considerations.
Let's review a simple example for averaging the the material relation , which is the part of equation of E.M.F (37) rewritten relatively to complex amplitudes (28) of filed. Suppose, that into each point of averaging area R.E.V. the electrical field is potential, i.e., [11] ), where is the dynamical potential and is the complex amplitude of dynamical potential. Then the joining between the complex amplitudes of the generalized dielectric displacement and the stretch of electric component field takes the form
(39)
According to the local macroscopic field approach into the area of averaging (R.E.V.) for each moment of time t the field is homogeneous, i.e., , where is the complex amplitude of external field. Then the expression for amplitude of the dynamic potential in this case have the view .
We can define the generalized complex dynamical dielectric constant (G.C.D.D.C.) in the Ω area (R.E.V.) on the base of the equality, which expresses the formal equivalence of material relations
(40)
According to definition of space average quantity (see Section 1, eqv. (6)) and reviewing relations we have
(41)
Here, it takes into account that the space averaged from the gradient of the dynamic potential will be
(42)
After substitution of (41) and (42) into the definition of G.C.D.D.C. (40), we get
(43)
here , where and is the effective complex dynamical dielectric constant and conductivity of the reviewed cell and t is the index which points on the light time dependence of physical quantity.
From the expression (43) it is follows, that quantity subject to neglect of dispersion phenomena into the material depends on constant frequency of external microwave irradiation, dielectric permeability and volume fraction of cell phases.
It should be noted that under the condition of weak variability of the volumetric characteristics of the porous material the E.G.C.D.D.C. can be reviewed, as constant physical quantity in the volume of averaging Ω (R.E.V.), which takes the constant into the time interval values.
Taking into account the definition of E.G.C.D.D.P. (39) into harmonic approach of local field (28) after applying described above the homogenization [9] on the mezoscopic level into range of R.E.V. considering approach of not interacting clusters we get (see Section 2, subsection 2, eqv. (37)) the averaged equation of field
(44)
where and are the light (slowly) changed functions of coordinate and are the complex amplitudes of Е.M.F. into the porous cell. Here time t have the sense of parameter with usage of which can be taken into account the moving of phases.
When obtaining the averaged field equations (44), a relatively simple method of finding the effective electro physical characteristics (the method of local spatial averaging) of a multiphase porous cell was used. The interesting comparative results of the dependence of the G.C.D.D.C. from the internal geometry or structure of the composite material for porous humidified sample are highlighted in the author's [2] article. For a more adequate description, it is necessary to take into account the dependences of the E.G.C.D.D.C. not only from the dielectric properties of the phases for porous cell, but also from their local microstructure [12], interaction between phase inclusions [10,13] and geometric shape or orientation [14].
Propagation of electromagnetic waves
According to the system of averaged equations E.M.F. (44) the wave equation for the Т.Е.М. (Transference Electromagnetic Wave) in the case of the monochromatic wave by the terms of the electric field strength into the composite body of low conductivity (C.B.L.C.) have the view
(45)
Here is the complex refractive index, is the effective wave vector into the porous (inhomogeneous) media, (where is the velocity of light) is the wave vector of this electromagnetic wave into vacuum, ω = 2πf is the angle frequency of E.M.F. (here f is the lineal frequency), µ0 and ε0 are correspondingly the magnate and electric constant into vacuum. The analytical solving of such equation is into details described by the author’s of this paper [15], where is demonstrated the possibility of applying of Wentzel-Kramers-Brillouin (W.K.B.) [16,17] method for founding the analytical solution of wave equation (45) into approach of slowly varying refractive properties of the T.E.M. wave.
Compatibility conditions of the electromagnetic field equations
The closed-form electrodynamic equations were obtained under the conditions of weak variation of the bulk (phase) and dielectric (wave) properties of a three-phase porous wetted material.
and (46)
As well as condition
which determines the possibility of using the effective macroscopic field approximation in the study (determination) of the effective electro physical properties of a porous material according to the method of local spatial averaging.
Here and is the wave vector and phase velocity of propagation the electromagnetic (T.E.M.) wave in the modelling media, is the effective value of refractive index, is the volume fraction f σ-phase, ω0 in the constant angle frequency the microwave field, l is the characteristic length of the volume Ω (R.E.V.) for space averaging.
Appendix
The simplest correlations between impulse-relaxation functions as well as the function of delaying for relation polarization and current can be received into harmonical approach of Е.М.F. (28) in the range of local averaging volume (R.E.V.) based on the macroscopic mean field approximation.
For this we will use the known [5] relation
(1)
here α = {P,J} is the index of vector notation for polarization P and current J. From this purpose we take the reviewed above integrals, which consist of impulse-relaxation function, and according to replacement (48), using the method of integration by the parts, let's reduce them to an equivalent form:
Case А. For the vector of polarization, we have gets
Case В. For the vector of current, we have gets
For electric field strengths at infinities, we assume the conditions of finiteness and equivalence of the field amplitude values (28) to the macroscopic field value , where . Here is the finite constant amplitude value.
When taking into account the harmonic approximation for electric field strengths within the R.E.V., the following relation holds: , where is the complex amplitude of field.
In the case of [А] at the replacing of variable for the integral into right part of equality we have gets the equivalent relation
After constituting the amplitude of harmonic field in the previous relation, we receive the appropriate equality
(2)
here is the average constant value of response function for polarization, for which obviously it is possible to match a certain fixed real time value with a known expression for the response function. When approximate equality is obtained, (2) is taken . Similarly, for the current vector in case [B] it can be shown that
(3)
Let us now consider the integral common to cases [A] and [B], which, by means of identical transformations, can be reduced to the approximate expression
here β = {P,J} is the index of the conventional designation of polarization vectors P and current J accordingly.
Then, according to the expressions for the polarization vectors (case [A]) and current (case [B]), we obtain the actual approximate relations
(4)
(5)
From which it is follows the expressions for relaxation functions, if you put into the relations (4) and (5) correspondingly.
The study explains the modeling of dielectric relaxation in porous, humidified materials that undergo microwave treatment. It provides valuable insights into how electromagnetic fields interact with multiphase porous media. The pulse relaxation method provides a clear understanding of dielectric properties. This understanding is essential for improving microwave processing techniques. This model is beneficial in materials science. It explains how dielectric relaxation functions, which help in designing and processing porous materials such as ceramics, polymers, and composites. The model also supports microwave-assisted drying, sintering, and curing involve uniform heating methods and strategies to prevent thermal damage. This concept could also benefit agriculture and environmental protection. Microwave radiation can measure moisture levels in porous soils and humid materials. It can also assess their behavior as dielectrics. This leads to better cleaning methods for soil and improved watering techniques for plants. Sensors that measure water and material saturation without causing harm work effectively for real-time field measurements. This modeling method can be improved to track dielectric changes in real time during industrial microwave operations. This would increase its practical value. This method, along with other ways to study materials, improves our understanding of how microwaves interact with complex porous structures.
The study of the unknown distribution of the electromagnetic field in composite structures is one of the fames or fundamental problems of mathematical physics. This is evidenced by many numbers of scientific works [18,19], which describe not only analytical models for calculating the field in relatively simple geometric structures, but also propose the numerical methods of modelling the distribution of electromagnetic field into inhomogeneous bodies. It is indeed difficult to predict the distribution of the electromagnetic field in porous wetted bodies. This is primarily due to the predominant or primary influence of the liquid phase. The distribution of liquid in the pores of the solid skeleton indicates a significant influence of surface wetting effects or adsorption in the near-surface layers of the solid skeleton. The electro-physical dielectric properties of bound or adsorbed water in near-surface layers differ significantly from the dielectric properties of free water known in the microwave irradiation range.The author of this article has attempted to propose a comprehensive theoretical approach to describing the phenomena of dielectric relaxation in porous wetted materials. This article considers the possibility of describing dielectric relaxation phenomena in layered composite bodies. It is not difficult to generalize the considered method for bodies of arbitrary geometric shape. The adequacy of the above mathematical relationships can only be confirmed by experimental research methods.
- Burak JY, Kushnir RM, editors. Modelling and optimisation in thermomechanics of electrically conductive heterogeneous bodies [Internet]. Lviv: Spolom; 2006;1–2:474.
- Hachkevych OR, Terlets’kyi RF, Holubets’ TV. Calculation of effective electrophysical characteristics of moistened porous materials. J Math Sci. 2010;168(5):699–711.
- Gawin D. Modelling coupled thermal-humidity phenomena in building materials and elements. ZN 853. Lodz: Lodz University of Technology Publishing House. 2000.
- Landau LD, Lifshitz EM. Electrodynamics of continuous media. Moscow: Nauka. 1982;632. Available from: https://ui.adsabs.harvard.edu/abs/1982MINTF...8.....L/abstract
- Böttcher CJF, Bordewijk P. Theory of electric polarization. Dielectrics in time-dependent fields. Amsterdam: Elsevier Scientific. 1978;561:2. Available from: https://api.pageplace.de/preview/DT0400.9780444600691_A23669214/preview-9780444600691_A23669214.pdf
- Gubkin AN. Physics of dielectrics. Theory of dielectric polarization in static and alternating electric fields. Moscow: Vysshaya Shkola. 1971;268.
- Riffe DM. Canonical models of dielectric response [Internet]. Utah State University; 2016;66. Available from: http://www.physics.usu.edu/riffe/bio/index.htm
- Korn G, Korn T. Handbook of mathematics. Moscow: Nauka. 1978;831. Available from: https://www.scirp.org/reference/referencespapers?referenceid=2241028
- Howes AH, Whitaker S. The spatial averaging theorem revisited. Chem Eng Sci. 1980;23(12):1613–23.
- Sihvola AH. Electromagnetic mixing formulas and applications. London: The Institution of Electrical Engineers. 1999; 284. Available from: https://www.bibliovault.org/BV.book.epl?ISBN=9780852967720
- Landauer R. Electrical conductivity in inhomogeneous media. In: Garland JC, Tanner DB, editors. Electrical transport and optical properties of inhomogeneous media. AIP Conf Proc. 1978;40:2–43. Available from: https://ui.adsabs.harvard.edu/abs/1978AIPC...40....2L/abstract
- Hilfer R, Widjajakusuma J, Biswal B. Macroscopic dielectric constant for microstructures of sedimentary rocks. Granul Matter. 2000;2:137–41. Available from: https://doi.org/10.1007/s100359900035
- Nettelblad B, Niklasson GA. Simple expressions of the dielectric response of suspensions in an electrolyte. J Colloid Interface Sci. 1996;181:165–8. Available from: https://www.academia.edu/48102416/Simple_Expressions_for_the_Dielectric_Response_of_Suspensions_in_an_Electrolyte
- Jones SB, Friedman SP. Particle shape effects on the effective permittivity of anisotropic or isotropic media consisting of aligned or randomly oriented ellipsoidal particles. Water Resour Res. 2000;36(10):2821–33. Available from: https://doi.org/10.1029/2000WR900198
- Holubets T, Terletskiy R, Yuzevych V. The analytical expressions to describe wave propagation and heat release during microwave treatment of a porous inhomogeneous plate based on the W.K.B. solution model. Adv Mater Sci. 2025;23(1):69–81. Available from: https://doi.org/10.2478/adms-2023-0005
- Katselenenbaum BZ. High-frequency electrodynamics. Fundamentals of mathematical apparatus. Moscow: Nauka. 1966;240.
- Godin OA. WKB approximation for atmospheric waves. J Fluid Mech. 2015;777:260–90. Available from: https://doi.org/10.1017/jfm.2015.367
- Takuma T, Tochaumnat B. Electric fields in composite dielectric and their application. London & New York: Springer Dordrecht Heidelberg. 2010;179. Available from: https://doi.org/10.1007/978-90-481-9392-9
- Rjlundzija BM, Djordjevic AR. Electromagnetic modeling of composite metallic and dielectric structures. Norwood: Artech House. 2002;408. Available from: https://books.google.co.in/books/about/Electromagnetic_Modeling_of_Composite_Me.html?id=zdR47nZ7oK8C&redir_esc=y